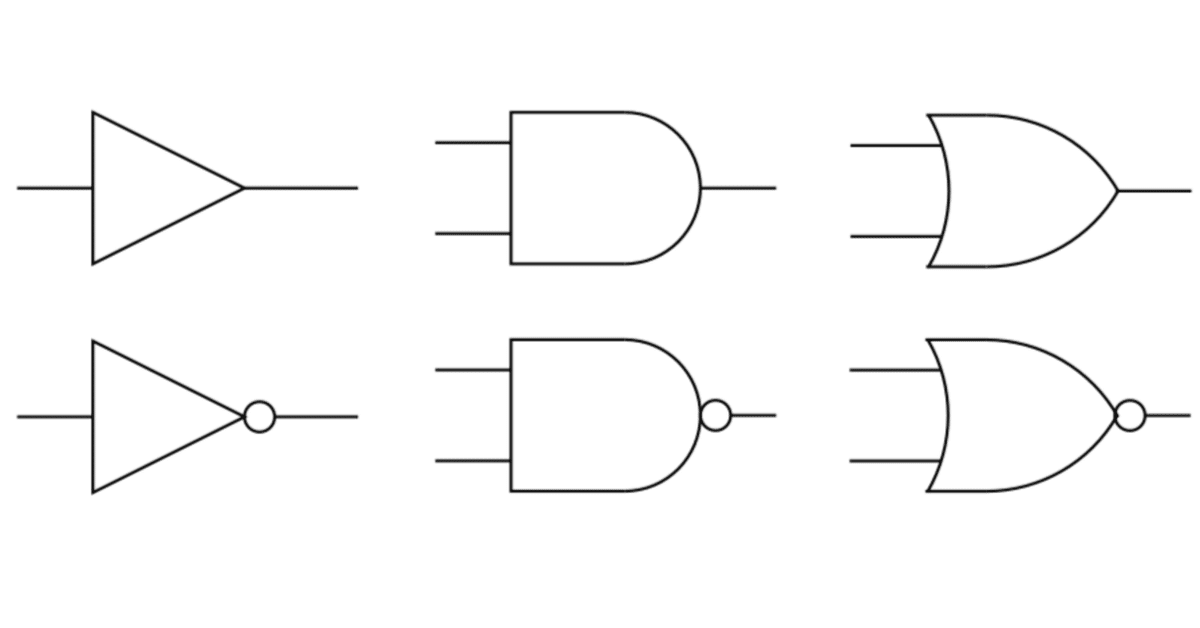
CMOS論理ゲートの構成
ここではCMOS論理ゲートの回路構成と動作について説明します.RTL からスタンダードセルを使って回路を合成する場合は論理ゲートの中身を知らなくても設計はできますが,知っておいて損はないと思います.この記事では組み合わせ論理回路 (combinational logic) のみを扱います.フリップフロップなど順序回路は扱いません.
1.論理演算
論理ゲートの前に,論理演算とは何かをまず説明しておきます.
1.1 論理演算 NOT,OR,ANDとブール代数
すべての変数が 0 と 1 のどちらかの値しか取らない世界を考えます.そのような変数に対する演算を考えましょう.まず1つの変数 $${A}$$ に対する演算 (単項演算) $${\overline{A}}$$ (Aバーと読みます)
$$
\begin{array}{|c||c|}
\hline
A & \overline{A} \\ \hline
0 & 1 \\
1 & 0 \\ \hline
\end{array}
$$
が考えられます.これは入力 $${A}$$ に対して $${\overline{A}}$$ は0 と 1 が反対になった結果になるます.これを論理否定 (NOT) と呼びます.また,上の表のように,変数の 0/1 とそのときの結果を表にしたものを真理値表 (truth table) と呼びます.論理否定は論理を反転させますから,2回適用すると元に戻ります.つまり,$${\overline{\overline{A}}=A}$$ です.
次に2つの変数 $${A}$$,$${B}$$ に対する二項演算を考えましょう.二項演算にはいろいろな種類が考えられますが,
$$
\begin{array}{|c|c||c|}
\hline
A & B & Y \\ \hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\ \hline
\end{array}
$$
のように,$${A}$$,$${B}$$ のどちらかが1 であれば出力 $${Y}$$ が1,言いかえると $${A}$$,$${B}$$ がともに 0 の場合のみ出力 $${Y}$$ が 0になる演算を $${Y=A+B}$$ と書くことにし,これを論理和 (OR) と呼びます.「AまたはB」ということです.
別の二項演算として,
$$
\begin{array}{|c|c||c|}
\hline
A & B & Y \\ \hline
0 & 0 & 0 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 1 \\ \hline
\end{array}
$$
も考えられます.これは $${A}$$,$${B}$$ がともに1のときのみ $${Y}$$ が1になる演算で,$${Y=A\times B}$$ と書き論理積 (AND) と呼びます.論理積は通常の積と同じく $${Y = A\cdot B}$$と書いたり,二項演算子を省略して $${Y=AB}$$ と書いたりします.「AかつB」ですね.
NOT,OR,AND があると,いろんな演算ができます.可補分配束になっているとか難しい理屈はさておき,このような系をブール代数 (Boolean algebra) と呼びます.プログラミング言語でも bool型 (だいたいは True と False の二値をとる) などででてくる名前です.
1.2 NAND,NOR
NOT,OR,AND が基本の論理演算になるわけですが,これらを組み合わせて別の論理演算を定義することもできます.例えば AND の NOT を取ると,真理値表は下のようになります
$$
\begin{array}{|c|c||c|}
\hline
A & B & Y=\overline{A\times B} \\ \hline
0 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\ \hline
\end{array}
$$
このような演算を NOT-AND で NAND と呼びます.日本語では否定論理積とか書くこともあるようですが,NAND で通用するでしょう.
OR の NOT を取ると,NOT-OR で NOR です.真理値表は以下.
$$
\begin{array}{|c|c||c|}
\hline
A & B & Y=\overline{A+B} \\ \hline
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 0 \\ \hline
\end{array}
$$
NAND と NOR は完全ゲートという性質をもっており,NAND もしくは NOR によってすべての論理式を表すことができます.
$$
\begin{array}{|c||c|c|}
\hline
A & \overline{A\times A} & \overline{A+A} \\ \hline
0 & 1 & 1 \\
1 & 0 & 0 \\ \hline
\end{array}
$$
のように,2つの入力に同じ変数を入れることで NOT が作れます.NOT ができれば $${Y=\overline{\overline{A\times B}} = A\times B}$$,$${Y=\overline{\overline{A + B}} = A+B}$$ で AND と OR が作れますから,すべての論理式が表せるというわけです.
1.3 排他的論理和 XOR
下のような真理値表も考えられます.OR に似ていますが,A と B がともに1 のときに 0 になります.
$$
\begin{array}{|c|c||c|}
\hline
A & B & Y=A\oplus B \\ \hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\ \hline
\end{array}
$$
このような論理演算を排他的論理和 (exclusive OR; XOR または EOR) と呼びます.NOT,OR,AND で表すと $${A\oplus B = (A\times\overline{B})+(\overline{A}\times B) = (A+B)\times(\overline{A}+\overline{B}) = (A+B)\times(\overline{A\times B})}$$ です.
1.4 論理関数
論理演算を組み合わせて,ある真理値表を実現する関数を論理関数と呼びます.
$$
\begin{array}{|c|c|c|c||c|}
\hline
A & B & \cdots & P & Y=f(A, B, \cdots, P) \\ \hline
0 & 0 & \cdots & 0 & 1 \\
0 & 0 & \cdots & 1 & 1 \\
\vdots & \vdots & & \vdots & \vdots \\
\end{array}
$$
任意の論理関数は NOT, AND, OR の組み合わせによって実現できます (完全性).真理値表から論理式を構成する方法にはカルノー図 (Karnaugh map) やクワイン・マクラスキー法 (Quine–McCluskey algorithm) などがありますが,長くなるのでここでは説明しません.
1.5 ド・モルガンの法則 (De Morgan's laws)
NOT,OR,AND の関係で重要なのがド・モルガンの法則です.
$$
\overline{A + B} = \overline{A}\times\overline{B},~~~~
\overline{A\times B} = \overline{A} + \overline{B}
$$
「『論理{和|積}の否定』は『否定の論理{積|和』と等価である」というのがド・モルガンの法則です.この法則は論理回路を考える上で多用しますので,覚えましょう.
2.論理回路の基礎
ある論理関数を実現する回路を論理回路,その中で論理演算を行なう回路素子を論理ゲート (logic gate)と呼びます.ここで説明するのは,出力が入力の組み合わせのみで決定される組み合わせ論理回路 (combinational logic) と呼ばれるものです.回路が過去の状態の「記憶」を持ち,記憶が出力に影響するような回路は順序論理回路 (sequencial logic) と呼びます.フリップフロップなどの記憶素子を含む回路が順序回路にあたります.
2.1 各種論理ゲート
各種論理演算に対応する論理ゲートの回路図記号は下の通りです.

素子の形が論理演算に対応し,○ が論理否定に対応します.
2.2 配線の分岐
論理回路は電気回路に準じた記法で描きます.配線の分岐は● (ソルダードット) で表します.信号は電圧の高低に対応しますので,下図のように,配線が分岐しても信号は変化しません.

2.3 配線の合流
それでは,電気回路のように信号線を合流させることはできるか,というと合流はCMOS論理回路では基本的には禁止です.ただし書きが2つついていますが,「CMOS論理回路では」というのは,論理ゲートをCMOS以外の方法で実現した場合,信号線の合流が使える場合があるからです.そのような場合,合流は OR となり,下図で言うと $${Y=P+Q}$$ となります.このように配線の合流が OR になるものを wired OR と呼び,TTL やマインクラフトのレッドストーン回路などは wired OR が使えます.wired OR が使えない場合,$${P\neq Q}$$ の場合に $${Y}$$ が決定不能になります.
次に「基本的には」と書いたのは,CMOS論理回路でも信号線を合流させることがあるからです.ただし,合流させる場合は後述する特殊な素子を使う必要があります.下図のような結線は不可です.

2.4 否定記号の移動とド・モルガンの法則
回路図記号で NOT,NAND,NOR には論理反転を表す○がついていますがこれは別に論理ゲートの出力だけでなく,入力にもつけることができます.下図のように入力につければ入力を反転させることができます.

そして同じ配線の上であれば,否定記号はどこにあっても一緒です.つまり,下図の回路は等価です.○は配線の上を移動することができるというわけです.

ただし,配線が分岐している場合には分岐先のすべてに○が表れることに注意しましょう.

さて,これをふまえてド・モルガンの法則を論理回路で書いてみます.
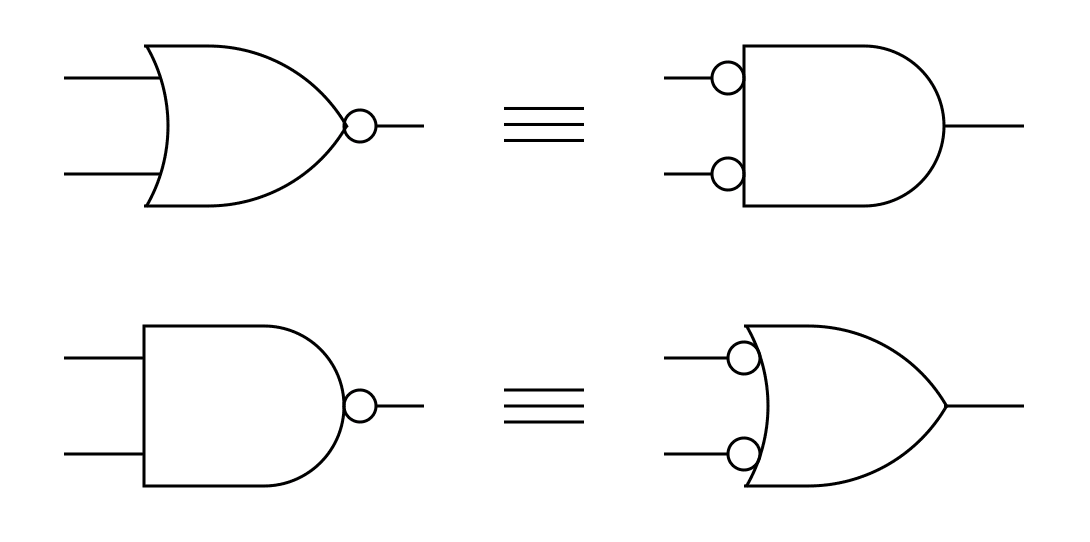
ド・モルガンの法則を使うと,論理ゲートの AND と OR を変換することができます.例えば $${Y=(A\times B) + (C\times D)}$$ は,ド・モルガンの法則を使って以下のように実現することができます.

AND と OR で構成するのが論理式そのままで簡単ですが,変換によって NAND のみで作ることができます.この変換は論理式としては同一ですが,CMOS回路で構成すると NAND のみで構成した方が優れた回路になります.
2.5 不定値 X
ここからはブール代数の枠をはずれたものについて説明します.基本的に論理回路はブール代数の論理関数を回路で実現するためのものですが,配線の合流のところで述べたように,回路では論理が決定できない状態を作り出すことができます.このように,0か1か決定できない状態を不定値と呼び,X と書きます.不定値は 0 かも知れないし1かも知れないしそのどちらでもない中途半端な電圧かも知れない,という状態です.不定値はおおむね以下の理由で発生します.
電源投入直後.記憶素子 (フリップフロップ) は電源が投入された瞬間には 0 になるか 1 になるか分かりません.ノイズなどランダムな要因によって 0 か 1 になります.よって電源投入直後のフリップフロップの値はすべて X になります.通常は非同期リセットによってすべての値を 0 に初期化して X を消します.
状態が決定できない回路.配線の合流や回路をループさせる (リングオシレータなど) ことで状態を決定できない回路を作ることができます.といっても,通常論理合成で論理回路を生成する場合そのような回路ができることはない (はず) ですし,手設計でそのような回路を作ったとしてもどこかのタイミングでツールがエラーか警告を出して教えてくれるでしょう.
X を含む真理値表は以下のようになります.
$$
\begin{array}{|c|c||c|c|c|c|c|c|}
\hline
A & B & \overline{A} & A+B & A\times B & \overline{A + B} & \overline{A\times B} & A\oplus B \\ \hline
\mathrm{X} & 0 & \mathrm{X} & \mathrm{X} & 0 & \mathrm{X} & 1 & \mathrm{X} \\
\mathrm{X} & 1 & \mathrm{X} & 1 & \mathrm{X} & 0 & \mathrm{X} & \mathrm{X} \\ \hline
\end{array}
$$
入力が X であっても出力が 0 か 1 に決まることもありますが,多くの場合出力も X になります.そのため,初期化などが不十分で X が残ってしまった場合,回路の一部や全部が X となり正常に動作しない場合があります.
3.論理ゲートの構成
ここでは電気回路によって論理ゲートを構成する方法を説明します.
3.1 スイッチ
論理ゲートは高い電圧 (HI) と低い電圧 (LO) のどちらかを出力する回路です.したがって,論理ゲートの実現方法として,電気的に制御されたスイッチによって出力端子を HI と LO のどちらかにつながるようにすればよいわけです.スイッチは電磁リレーでも真空管でもトランジスタでも構いません.
スイッチとして考えられるのは,制御電圧が HI のとき閉じるものと,制御電圧が LO のときに閉じるものです.下の図のように描き分けることにします.○が論理反転を表しています.

3.2 抵抗とスイッチによる論理ゲート
スイッチは開と閉の2つの状態をもつわけなので,スイッチを1つ使えば 0 と 1 の状態を実現できます.例えば下図は NOTゲートです.

スイッチを VSS (LO) との接続に使った場合,それだけだと VDD (HI) につなぐ経路ができないので VDD と出力 $${Y}$$ は抵抗で接続します.入力 $${A}$$ が LO であればスイッチは開くので,抵抗が出力 $${Y}$$ の電位を HI に引き上げます (プルアップ; pull-up).$${A}$$ が HI の場合,スイッチが閉じます.このとき出力 $${Y}$$ は抵抗を介して VDD にもつながっていますが,スイッチが閉じたときの抵抗は理想的には 0 ですから,出力 $${Y}$$ は LO に引き下ろされます (プルダウン; pull-down).
AND・OR の論理は,スイッチの直列接続・並列接続によって実現されます.下図がNANDとNOR回路です.
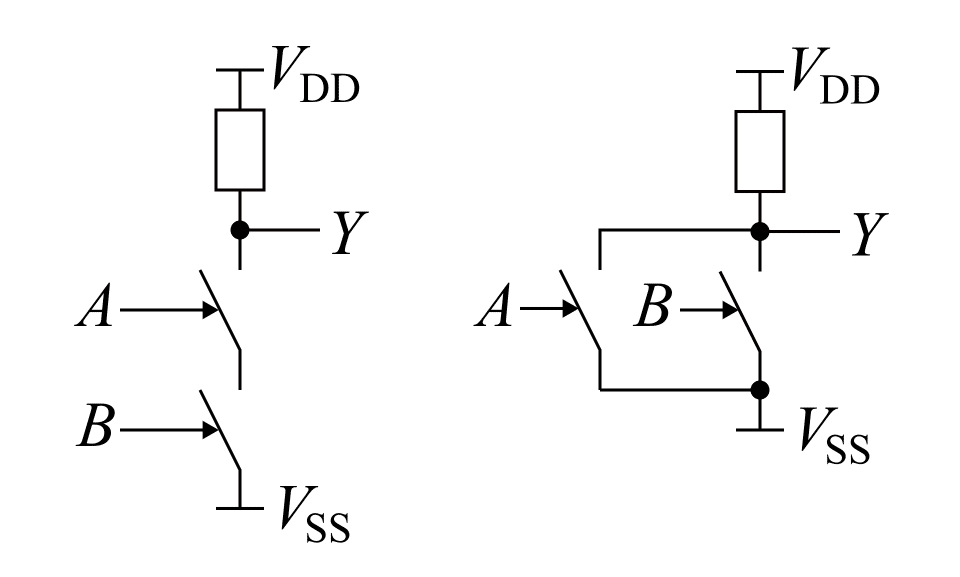
スイッチが直列に接続された場合,両方のスイッチが閉じたときのみその経路はつながります.これが AND の論理に相当します.逆に並列になっている場合は,どれか1つのスイッチが閉じていれば経路がつながるので,これが OR に相当します.
この方式は入力1つにスイッチ1つで実現できるのでスイッチの数を少なくすることができますが,欠点もあります.
定常電流が流れる.下図のようにスイッチが閉じている間,VDD から VSS に向かって電流が流れ続けます.これによって消費電力が増えます.抵抗を介してはいますが,論理ゲートの数が増えていくと抵抗が並列に並ぶ数が増えるわけですから,合成抵抗はどんどん下がっていき,流れる電流はどんどん大きくなります.
速度の問題.スイッチの抵抗は十分に低いことが期待される一方,抵抗の抵抗値は固定です.抵抗が大きいということは電流が流れにくいため,下図の回路では出力 HI → LO は速いが LO → HI は遅い,ということが起こります.論理ゲートの動作速度については別記事で解説します (たぶん,いずれ).

3.3 スイッチのみによる論理ゲート
スイッチの数を少なくする構成では,プルアップかプルダウンのどちらかを抵抗,他方をスイッチによって構成していました.この抵抗が固定であるが故に電力や速度の問題が生じるので,抵抗を使わずにスイッチだけで構成することを考えます.
下図のようにプルアップとプルダウン両方にスイッチを使えば NOT ゲートができます.ポイントは入力 $${A}$$ を異なる種類のスイッチの制御に使い,プルアップとプルダウンのどちらか一方しか閉じないようにしていることです.この「1つの入力で2つのスイッチが制御されており,どちらか1つしか閉じない」という性質が相補的 (complementary) ということであり,スイッチが MOSFET で作られているのが CMOS (Complementary MOS) です.

AND・OR を作るには,プルダウン側が並列ならプルアップ側は直列,のようにプルダウン側とプルアップ側で直列・並列が入れ替わります.下図が NAND と NOR です.例えば NAND ゲートで考えると,プルダウン側がすべて閉じているときのみプルアップ側は開,プルダウン側が1つでも開になっているときはプルアップしないといけない訳なので,プルダウン側が直列ならプルアップ側は並列となるわけです.

3.4 スイッチのみで構成した場合の出力の4状態
一旦相補的な構成は忘れることにして,スイッチの組み合わせで論理ゲートが構成されている場合を考えます.スイッチが直列になっていようと並列になっていようと (またはその組み合わせであろうと),出力は VDD につながっているかつながっていないか,VSS につながっているかつながっていないか,の組み合わせで合計4つの状態を取ります.
プルアップが開,プルダウンが閉: 出力は LO
プルアップが閉,プルダウンが開: 出力は HI
プルアップとプルダウン両方が開: 出力はハイインピーダンス (Z)
プルアップとプルダウン両方が閉: 出力は不定,というか壊れる
論理ゲートとしては LO と HI の2状態でよい,というか2状態のどちらかでないと困るわけですが,「両方開」「両方閉」という状態になりうるのです.論理ゲートの回路を考える際にはこの残り2状態についても知っておく必要があります.
両方開の状態をハイインピーダンス (high-impedance) と呼び,Z と書きます.これについては次節で説明します.両方閉の状態には名前はついていません.というのも,壊れるからです.プルアップ・プルダウン両方が閉ということは VDD から VSS までの経路がスイッチで短絡された状態です.抵抗とスイッチで論理ゲートを作ったときも VDD から VSS への経路は存在していましたが,あちらは必ず抵抗が入っています.スイッチのみでつながった場合はいわば保護抵抗なしで LED を電源に直結したようなもので,焼き切れます.焼けないにしても電源が地絡しているので,まともな動作はしません.
3.5 ハイインピーダンス
出力ハイインピーダンスは通常の論理演算では使いませんが,ハイインピーダンスを作れる論理ゲートを使うことで,2節で「基本的に禁じ手」と書いた配線の合流ができるようになります.
論理ゲートの出力を合流させてはならないのは,下図のような状態を防ぐためです.

ただ,ラッチを作る場合など論理ゲートの出力同士をつなぎたい場合も存在します.その場合,出力がハイインピーダンスの論理ゲートとであれば出力同士をつなぐことができます.Z があるとすると,下図のような配線の合流に対して真理値表を書くことができます.

$$
\begin{array}{|c|c||c|}
\hline
A & B & Y \\ \hline
0 & 0 & 0 \\
0 & 1 & \mathrm{X} \\
0 & \mathrm{Z} & 1 \\
1 & 0 & \mathrm{X} \\
1 & 1 & 1 \\
1 & \mathrm{Z} & 1 \\
\mathrm{Z} & 0 & 0 \\
\mathrm{Z} & 1 & 1 \\
\mathrm{Z} & \mathrm{Z} & \mathrm{X} \\ \hline
\end{array}
$$
ハイインピーダンスを作る回路構成として,おおきく2つの方法があります.VDD/VSS を切り離す方法と,出力端子を切り離す方法です.

この論理ゲートの真理値表は以下の通りです.$${B}$$ が 0 のとき,出力がハイインピーダンスになります.出力が 0,1,Z の3状態をとることから,トライステートバッファ (tri-state buffer) と呼んだり,クロックドインバータ (clocked inverter) と呼んだりします.
$$
\begin{array}{|c|c||c|}
\hline
A & B & Y \\ \hline
0 & 0 & \mathrm{Z} \\
0 & 1 & 1 \\
1 & 0 & \mathrm{Z} \\
1 & 1 & 0 \\ \hline
\end{array}
$$
4.CMOS論理ゲート
いよいよ MOSFET で論理ゲートを作ります.基本的には前節のスイッチを pMOSFET,nMOSFET に置き換えればよいわけですが,pMOSFET と nMOSFET は理想スイッチではありませんのでちょっと制約があります.
4.1 MOSFETの特性
MOSFET はゲート-ソース間電圧 $${V_{\text{GS}}}$$ とドレイン-ソース間電圧 $${V_{\text{DS}}}$$ によって制御される素子で,回路図記号と各電圧は下図の通りです.

端子と電圧の方向に注意してください.nMOS ではソースが最も低い電位で,pMOSではソースが最も高い電位です.そのため,図では pMOS はソースSを上側に描いています.$${V_{\text{GS}}}$$ はソース電位を基準としたゲート電位なので,nMOSでは $${V_{\text{GS}}\geq 0}$$,pMOS では $${V_{\text{GS}}\leq 0}$$ となります.線形領域とか飽和領域とかの話はさて置き,しきい値電圧 $${V_{\text{th}}}$$ に対して $${\left|V_{\text{GS}}\right| > \left|V_{\text{th}}\right|}$$ になるとチャネルが形成され,ドレインとソース間が導通します.
よって,3節で使ったスイッチの記号との対応は下のようになります.

スイッチの○とpMOSのゲートについた○ はともに論理反転を表します.
4.2 スイッチとしての MOSFET
残念ながら,MOSFET は常に理想スイッチとして扱えるわけではありません.下図は,nMOSとpMOSをそれぞれプルアップとプルダウンに使ったときの端子と電位の関係を表しています.

これらの組み合わせがどのように動くか考えてみます.nMOS でプルアップする場合,ドレインの電位は必ずソース電位よりも高いので,ドレインが電源 VDD に接続されます.そうすると,ソースの電位は $${V_{\text{DD}} - V_{\text{DS}}}$$,制御端子 (ゲート) の電位は $${V_{\text{DD}} - V_{\text{DS}} + V_{\text{GS}}}$$ になります.プルアップですので,ソース電位を $${V_{\text{DD}}}$$ まで引き上げたいわけですが,MOSFET がスイッチとして閉の状態にあるためには $${V_{\text{GS}} > V_{\text{th}}}$$ である必要があります.制御電圧 $${V\leq V_{\text{DD}}}$$ ですから,$${V = V_{\text{DD}} = V_{\text{DD}} - V_{\text{DS}} + V_{\text{GS}}}$$ より $${V_{\text{DS}} = V_{\text{GS}}}$$,つまり $${V_{\text{DS}} > V_{\text{th}}}$$ である必要があり,ソース電位は $${V_{\text{DD}} - V_{\text{th}}}$$ までしかプルアップできません.これ以上ソース電位を上げようとすると MOSFET がオフ (スイッチ開) の状態になってしまいます.このため,nMOS はプルアップに使おうとすると,目標値よりしきい値電圧 $${V_{\text{th}}}$$ だけ低い電位までしか引き上げられない「弱い」プルアップしかできません.
一方で nMOS をプルダウンに使った場合はどうなるかというと,この場合はソース電位が LO電位 $${V_{\text{SS}}}$$ に固定されます.$${V_{\text{GS}}}$$ と $${V_{\text{DS}}}$$ は独立していますから,$${V_{\text{DS}} = 0}$$ までドレイン電位を下げても問題なく $${V_{\text{GS}}>V_{\text{th}}}$$ を維持することができる「強い」プルダウンができます.
pMOS の場合は逆で,強いプルアップと弱いプルダウンになります.このため,nMOSはプルダウン,pMOSはプルアップに使う,という制限があります.
4.3 CMOS論理ゲート
説明がとんでもなく長くなりましたが,ここまでの内容をふまえて CMOS論理ゲートを構成すると,下図のようになります.「nMOSはプルダウン,pMOSはプルアップ」という制約があるため,AND・OR よりも NAND・NOR の方が簡単な構成になります.

AND・OR が必要な場合はド・モルガンの法則を用いて NAND・NOR に変換する,AOI (AND-OR-Invert) / OAI (OR-AND-Invert) といった複合ゲートを使うなどします.論理式をどのような形にするか,という話は長くなるのでここではしません.論理の簡単化とか積和標準形とか和積標準形とかを勉強しましょう.
また,ハイインピーダンスを作るために信号線を切断するスイッチは下図のように実現します.この回路をトランスミッションゲート (transmission-gate; TG) と呼びます.

5.まとめ
論理回路の基本として,組み合わせ論理回路と論理ゲートの構成方法を説明しました.次の記事では論理ゲートの性能について説明しようと思います (たぶん,いずれ).
この記事が気に入ったらサポートをしてみませんか?
