ChatGPT(GPT-4)にマルコフ連鎖モンテカルロ法(MCMC)を解説してもらいました
はじめに
この記事は、ChatGPT(GPT-4)から、マルコフ連鎖モンテカルロ法(MCMC: Markov Chain Monte Carlo)を解説してもらい、理解を深めようと試みた記録です。
記事のほとんどがChatGPTとの会話のコピーなので、数学的解釈、プログラミングの間違いなどあるかもしれませんが予めご了承ください。
ChatGPTとの会話
ここから先は、実際の会話のコピーです。質問文は太字にしています。
[質問]
以下の点について教えてください。
モンテカルロ法とは何ですか?
MCMCとは何ですか?
MCMCはモンテカルロ法に比べ、どんな点で優れていますか?
300字程度で簡潔に教えてください。
[回答]
モンテカルロ法は、乱数を利用して問題の解を近似する確率的なシミュレーション手法です。統計的な試行を繰り返すことで、積分や最適化などの複雑な問題を解決します。
MCMC(マルコフ連鎖モンテカルロ)は、モンテカルロ法の一種で、マルコフ連鎖を利用して目的の確率分布からサンプリングする手法です。これにより、高次元空間や複雑な確率分布でも効率的にサンプリングが可能になります。
モンテカルロ法に比べ、MCMCは以下の点で優れています。
高次元空間や複雑な確率分布に対応可能。
逐次的にサンプルを生成するため、収束が早く、効率的。
モンテカルロ法は確率的シミュレーション手法で、乱数を使って問題解決を試みます。一方、MCMCはモンテカルロ法の一種で、マルコフ連鎖を用いて目的の確率分布からサンプリングします。MCMCは高次元空間や複雑な分布に対応でき、効率的なサンプリングが可能です。
[質問]
モンテカルロ法の例を確認したいので、以下の通りにPythonコードを作成してください
scipyを使って[-1, 1]の範囲で一様乱数を1000個生成し、円周率を推定するコードを書いてください。
生成された乱数を散布図に示し、そこに半径1の円を描画してください。
最後に円の内側の個数と外側の個数、円周率の推定値をprint関数で出力してください。
[回答]
以下のPythonコードは、モンテカルロ法を用いて円周率を推定します。また、散布図と半径1の円を描画し、円の内側と外側の点の個数と円周率の推定値を出力します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
# 一様乱数の生成
random_points = uniform.rvs(-1, 2, size=(1000, 2))
# 円の内外の点の分類
inside_circle = np.sum(np.square(random_points), axis=1) <= 1
outside_circle = np.sum(np.square(random_points), axis=1) > 1
# 円周率の推定
pi_estimate = np.sum(inside_circle) / len(random_points) * 4
# 散布図と円の描画
plt.scatter(random_points[inside_circle, 0], random_points[inside_circle, 1], color='blue', label='Inside circle')
plt.scatter(random_points[outside_circle, 0], random_points[outside_circle, 1], color='red', label='Outside circle')
theta = np.linspace(0, 2 * np.pi, 100)
x = np.cos(theta)
y = np.sin(theta)
plt.plot(x, y, label='Unit circle')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Monte Carlo Estimation of Pi')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
# 結果の出力
print(f"Number of points inside the circle: {np.sum(inside_circle)}")
print(f"Number of points outside the circle: {np.sum(outside_circle)}")
print(f"Estimated value of pi: {pi_estimate}")このコードを実行すると、円周率の推定値が得られます。ただし、推定値は乱数に依存するため、実行のたびに結果が変わります。
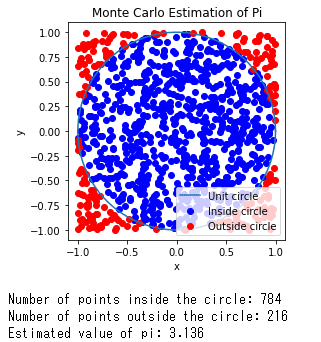
[補足]
円の内側の個数(青)を、生成した乱数の個数(青+赤)で割ると、π/4となります。
[質問]
上のコードを書き変えて、サンプルが増えるにつれて推定の精度が上がる様子を確認させてください。 乱数を生成する数を、10から10ずつ増やして1000になるまで繰り返し、それぞれの推定値をグラフにプロットしてください。
[回答]
以下のPythonコードは、サンプル数を10から1000まで10刻みで増やし、それぞれの推定値をグラフにプロットすることで、サンプルが増えるにつれて推定の精度が上がる様子を確認できます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
sample_sizes = range(10, 1001, 10)
pi_estimates = []
for n_samples in sample_sizes:
# 一様乱数の生成
random_points = uniform.rvs(-1, 2, size=(n_samples, 2))
# 円の内外の点の分類
inside_circle = np.sum(np.square(random_points), axis=1) <= 1
# 円周率の推定
pi_estimate = np.sum(inside_circle) / n_samples * 4
pi_estimates.append(pi_estimate)
# 推定値のプロット
plt.plot(sample_sizes, pi_estimates, marker='.', linestyle='-', label='Estimated Pi')
plt.axhline(y=np.pi, color='r', linestyle='--', label='True Pi')
plt.xlabel('Number of Samples')
plt.ylabel('Estimated Pi')
plt.title('Convergence of Monte Carlo Estimation of Pi')
plt.legend()
plt.show()このコードを実行すると、サンプル数が増えるにつれて推定値が真の円周率に収束していくことが確認できます。
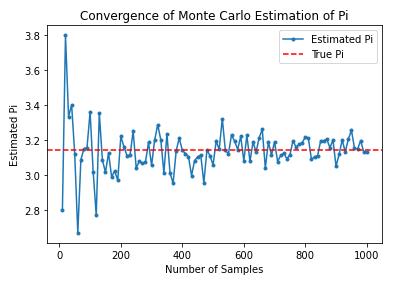
[質問]
モンテカルロ法で標準正規分布の積分の推定をしたとき、乱数のサンプルサイズと積分範囲が推定精度にどのように影響するかについて調べます。以下の通りにPythonコードを作成してください
乱数を生成する数を、10から10ずつ増やして1000になるまで繰り返し、それぞれの推定値をリストに格納します。
積分範囲を広げて、1を実行します。
積分範囲を10, 100, 1000, 10000と増やしていくごとに、推定値の収束がどのように変化するか比較できるようにグラフに出力してください。
[回答]
以下のPythonコードは、標準正規分布の積分の推定をモンテカルロ法で行い、乱数のサンプルサイズと積分範囲が推定精度にどのように影響するかを調べます。積分範囲を10, 100, 1000と増やしていくごとに、推定値の収束の様子をグラフで比較できます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, uniform
def monte_carlo_integration(n_samples, range_limit):
# 一様乱数の生成
random_points = uniform.rvs(-range_limit, 2 * range_limit, size=n_samples)
# 標準正規分布の確率密度関数を適用
function_values = norm.pdf(random_points)
# 積分の推定
integral_estimate = np.mean(function_values) * 2 * range_limit
return integral_estimate
sample_sizes = range(10, 1001, 10)
range_limits = [10, 100, 1000]
plt.figure(figsize=(10, 6))
for range_limit in range_limits:
integral_estimates = [monte_carlo_integration(n_samples, range_limit) for n_samples in sample_sizes]
plt.plot(sample_sizes, integral_estimates, marker='.', linestyle='-', label=f'Range limit: {range_limit}')
# 真の積分値(標準正規分布の全範囲における確率は1)
true_integral = 1
plt.axhline(y=true_integral, color='r', linestyle='--', label='True Integral')
plt.xlabel('Number of Samples')
plt.ylabel('Estimated Integral')
plt.title('Convergence of Monte Carlo Integration for Standard Normal Distribution')
plt.legend()
plt.show()このコードを実行すると、積分範囲が広がるにつれて推定精度の収束が遅くなることが確認できます。また、サンプルサイズが増えるにつれて推定精度が向上することもわかります。
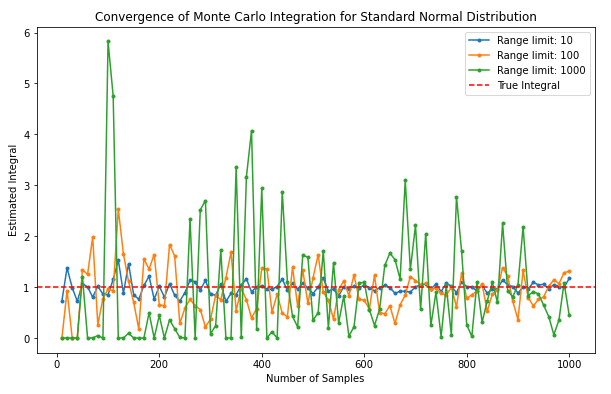
[補足]
積分範囲が±10(青)、積分範囲が±100(黄)、積分範囲が±1000(緑)です。積分範囲が広がると、真の積分結果(赤)を推定することが難しくなっている様子を示しています。
[質問]
なぜ積分範囲が広がるにつれて推定精度の収束が遅くなるのですか?100字以内で説明してください。
[回答]
積分範囲が広がると、一様分布から生成される乱数の範囲も広がります。その結果、標準正規分布のピーク付近の重要な領域に相対的に少ないサンプルが生成されることになります。これが推定精度の収束を遅くする主な要因です。
[質問]
MCMCは収束が早く、効率的と最初に説明していただきましたが、MCMCならこの問題を解決できますか?
[回答]
はい、MCMCはこの問題の解決に役立ちます。モンテカルロ法では一様分布からの乱数が必ずしも目的関数に対して効率的でないため、収束が遅くなることがあります。しかし、MCMCはマルコフ連鎖を利用して目的の確率分布(この場合は標準正規分布)から直接サンプリングするため、重要な領域に自動的に焦点を当てることができます。
これにより、MCMCは収束が早く、効率的なサンプリングが可能になります。特に高次元空間や複雑な確率分布の場合、MCMCは従来のモンテカルロ法よりも優れた性能を発揮します。ただし、MCMCの収束性を評価する方法は通常のモンテカルロ法と異なり、専門的な知識が必要です。
[質問]
MCMCのアルゴリズム「Metropolis-Hastings」を使用し、結果が標準正規分布に収束する様子を示します。 繰り返し回数を[100, 1000, 10000]と変化させたときに、それぞれの生成されたサンプルが標準正規分布に収束している様子を確認するため、3つのヒストグラムを横に並べて表示してください。
[回答]
以下のPythonコードは、Metropolis-Hastingsアルゴリズムを使用して、結果が標準正規分布に収束する様子を示します。繰り返し回数が[100, 1000, 10000]で変化するときの生成されたサンプルのヒストグラムを横に並べて表示します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def metropolis_hastings(iterations, proposal_stddev):
samples = np.zeros(iterations)
current_sample = np.random.rand()
for i in range(1, iterations):
proposal_sample = current_sample + np.random.normal(0, proposal_stddev)
acceptance_probability = min(
1,
norm.pdf(proposal_sample) / norm.pdf(current_sample)
)
if np.random.rand() < acceptance_probability:
current_sample = proposal_sample
samples[i] = current_sample
return samples
iterations_list = [100, 1000, 10000]
proposal_stddev = 1
plt.figure(figsize=(15, 5))
for index, iterations in enumerate(iterations_list):
samples = metropolis_hastings(iterations, proposal_stddev)
plt.subplot(1, 3, index + 1)
plt.hist(samples, bins=30, density=True, label='Generated Samples')
x = np.linspace(-4, 4, 100)
plt.plot(x, norm.pdf(x), label='Standard Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.title(f'Metropolis-Hastings with {iterations} Iterations')
plt.legend()
plt.show()このコードを実行すると、繰り返し回数が増えるにつれて、生成されたサンプルが標準正規分布に収束している様子が確認できます。ただし、収束には適切な提案分布の選択が重要です。この例では、標準偏差が1の正規分布を提案分布として使用しています。

最後に
冒頭にも記しましたが、AIとの対話であるため、数学的解釈やプログラミングの間違いなどあるかもしれません。
全くの知識ゼロから、このやり方で勉強すると間違いに気付けない恐れはあるかなと思います。ある程度の前知識があって、良い出力を促すように考えながら、生成したコードを実行しながら進めると理解が深まるかもしれないですね。
この記事が気に入ったらサポートをしてみませんか?
