生命現象を実装してみよう〜パターン形成と細胞分化を例に〜

2023年12月9日 18:42

「発生」という名の超常現象

生物の発生という現象は、極めて神秘的であり、これほど面白い物理現象は他には存在しないとさえ思っている（少し盛った）。
少々歴史的な話をするならば、発生生物学の世界において、「前成説」と「後成説」という２つの対立した仮説が存在していた時期がある。前者は、「各器官は生殖細胞の中に小さな形であらかじめ収まっていて（いわゆるホムンクルスと呼ばれる）、発生の過程でそれらが拡大することによって成体が形成される」とする考えである。一方で後者は、「各器官が各世代で一から新たにつくられる」とする考えである。今となっては、「前成説」が誤りであり「後成説」が正しいということは、中学生や高校生でも知っているほどの常識となっている（はずだ）が、その当時においては前成説がある程度支持されていたのも不思議ではないと思う。我々の体は、実は元々0.1mm程度の、脂質膜で包まれたタンパク質の塊であったという事実は現代でも俄には信じがたい。

生命体の組織や器官の形成は、本質的には主に２つの要素で実現される。
１つはモルフォゲンの濃度勾配である。モルフォゲンとは、発生過程においてその濃度勾配によって、器官の形態形成を司る生体内の化学物質の総称である。ショウジョウバエにおいて、その前後軸がbicoidやnanos、hunchbackといったモルフォゲンタンパク質によって決定され、体軸形成が誘導されることは（少なくとも生物学界隈では）有名である。
もう１つの要素は遺伝子発現制御である。先ほどのモルフォゲンが細胞集団（組織）のスケールであったのに対し、遺伝子発現制御は細胞内での現象である。これはモルフォゲンの濃度勾配や隣接する細胞などから受ける刺激を、各細胞が受容体などを介して感知、その情報によってクロマチン修飾、DNAメチル化といったエピゲノム修飾や、転写因子による発現調節を通して、発現されるタンパク質の種類や量、タイミングが巧妙に調整される仕組みである。

**モルフォゲンの濃度勾配と遺伝子制御ネットワークによる、位置依存的な遺伝子発現の例**
例えば、右側の図では、Shh（ソニックヘッジホッグ）というモルフォゲンの勾配が、前後軸方向と背腹軸方向に存在していた時に、上のグラフで示されているような遺伝子制御ネットワークが存在することで、位置依存的にNkx2.2、Olig2、Pax6の発現量が変化することが分かっている。またPax6をノックアウトした場合にはその分布が変化することも示されている。
（Kicheva A, Briscoe J. Control of Tissue Development by Morphogens. Annu Rev Cell Dev Biol. 2023 Oct 16;39:91-121. doi: 10.1146/annurev-cellbio-020823-011522. Epub 2023 Jul 7. PMID: 37418774. より引用）

発生過程において、着目すべき点の１つは間違いなくそのロバスト性（頑健性）である。もう少し簡単に言い換えると、ゆらぎやノイズに対する"強さ"である。しばしば生体は機械に喩えられるが、この点においては、生体は機械よりも遥かに優れたシステムであると言って良いだろう。
第一に、生体と機械とではそのS/N比が大きく異なる。要するに生体システムはノイズに溢れているのである。このノイズの正体は、意図しない力学的な揺動や、生体分子同士が反応する際などに避けることのできない熱力学的なもの、生体分子のミクロスコピックなスケールによる非平衡的なゆらぎや量子的ゆらぎなど、さまざまなものが考えられる。
このような環境の中、生体分子や細胞が如何にして、その相互作用の中で情報を伝達し、頑健かつ可塑的な生体システムを構築、維持しているのか、という点に私は非常に興味がある。

パターン形成の数理

拡散方程式

モルフォゲンは、その濃度勾配で組織形成を誘導できる「魔法の粉」のように思えるが、所詮は化学物質にすぎない。ゆえに、流体中での運動は原則として拡散方程式に支配される。

手始めに、一次元空間上でモルフォゲンの挙動を考えよう。位置$${x}$$、時刻$${t}$$における分子の濃度を$${c(x,t)}$$とおくと、$${x}$$〜$${x+\Delta x}$$間における時間$${\Delta t}$$間の物質量変化は

$$
(c(x,t+\Delta t)-c(x,t))\Delta x
$$

である。また、単位時間あたりに単位断面積を通過する分子数を流速密度$${J(x)}$$と定義すると、$${x}$$〜$${x+\Delta x}$$間における$${\Delta t}$$間の物質量変化は

$$
(J(x)-J(x+\Delta x))\Delta t
$$

である。
ここで濃度の時間変化と流入出の収支は釣り合っている必要があるので、

$$
\frac{c(x,t+\Delta t)-c(x,t)}{\Delta t}=\frac{J(x)-J(x+\Delta x)}{\Delta x}
$$

を得る。ここで極限を取ると

$$
\frac{\partial c(x,t)}{\partial t}=\frac{\partial J(x)}{\partial x}
$$

を得る。
ここでフィックの第１法則

$$
J=-D\frac{\partial c(x,t)}{\partial x}
$$

より（$${D}$$は拡散定数）

$$
\begin{array}{} \frac{\partial c(x,t)}{\partial t}&=&\frac{\partial}{\partial x}(D\frac{\partial c(x,t)}{\partial x})\\\ &=& D\frac{\partial^2 c(x,t)}{\partial x^2} \\\ &=& D \nabla^2 c(x,t) \end{array}
$$

を得る。これが一次元の拡散方程式である。
ちなみに同様の議論により三次元の拡散方程式

$$
\frac{\partial c(x,y,z,t)}{\partial t}=D \nabla^2 c(x,y,z,t)
$$

を得る。

では次に、一次元の拡散方程式の（解析）解を求めてみよう。この式は時間に関して１階、位置に関して２階の偏微分方程式なので、ある時刻における$${c(x,t)}$$の条件が１つ、ある位置における$${c(x,t)}$$の条件が２つ必要となる。
したがって初期条件として

$$
C(x,0)=C_0(x)
$$

$$
C(\pm \infty ,t)=0
$$

を設定する。

まず、$${c(x,t)}$$のフーリエ変換は

$$
c(x,t)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \hat{c(k,t)} e^{ikx} dk
$$

であるから、これを拡散方程式に代入すると

$$
\int_{-\infty}^{\infty} (\frac{d \hat{c}}{dt} +Dk^2 \hat{c})e^{ikx} dk =0
$$

任意の$${x}$$について上式が成り立つためには被積分関数が0である必要があるから

$$
\frac{d \hat{c}}{dt} +Dk^2 \hat{c}=0
$$

を得る。この常微分方程式の解は変数分離法を用いて容易に解ける。

$$
\hat{c(k,t)} = A(k) e^{-Dk^2 t}
$$

これを元々のフーリエ変換の式に代入することにより

$$
c(x,t)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} A(k) e^{ikx-Dk^2 t} dk
$$

次に初期条件を考慮しよう。$${C(x,0)=C_0(x)}$$より

$$
c_0(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} A(k) e^{ikx} dk
$$

フーリエ逆変換により

$$
A(k)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} c_0(x) e^{ikx} dx
$$

である。したがって

$$
\begin{array}{} c(x,t)&=&\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} dk \int_{-\infty}^{\infty} dx' c_0(x') e^{ik(x-x')-Dk^2t} \\\ &=& \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} dx' c_0(x') e^{-\frac{(x-x')^2}{4Dt}}[ \int_{-\infty}^{\infty} dk e^{-Dt {k-\frac{i(x-x')}{2Dt}}^2 }] \end{array}
$$

を得る。ここでガウス積分を用いると

$$
c(x,t)=\frac{1}{2 \sqrt{ \pi Dt }} \int_{-\infty}^{\infty} dx' c_0(x') e^{-\frac{(x-x')^2}{4Dt}}
$$

と書き換えられる。これによって任意の初期条件$${c_0(x)}$$に対する一次元の拡散方程式の解を得られた。

例えば初期条件として

$$
c_0(x)=\delta (x)
$$

を設定する。このとき、δ関数の性質により

$$
c(x,t)=\frac{1}{2\sqrt{\pi Dt}}e^{-\frac{x^2}{4Dt}}
$$

という解を得る。この式はガウス分布と同じ形をしているので覚えやすいだろう。

また別の条件として、一次元空間上の両端における物質濃度が時間によらず一定であると仮定する。具体的には

$$
c(0,t)=c_{max}
$$

$$
c(L,t)=c_{min}
$$

という条件を課す。定常状態$${\frac{\partial c}{\partial t}=0}$$を考えることにすると、拡散方程式の解は

$$
c(x)=(c_{min}-c_{max})\frac{x}{L}+c_{max}
$$

であることは容易にわかるだろう。つまり、定常状態では線形的な勾配を示す。この結果からかつての発生生物学者は、各細胞が周囲のモルフォゲン濃度を感知し、単純にその濃度に応じて特定の種類の細胞へ分化するのではないかと考えた（これはフランス国旗に見立てて「三色旗問題」と呼ばれる）。しかし、今導出した解析解を見てわかる通り、このモデルにおいて、モルフォゲン濃度は系のスケール$${L}$$に依存している。これでは、個体の成長やゆらぎに大きく影響されてしまうが容易に想像されるだろう。

三色旗問題
（https://bastiani.biology.utah.edu/courses/3230/DB%20Lecture/Lectures/a8Pattern.htmlより引用）

そこで別の状況として、全ての空間上で濃度に比例した分解が行われる場合を考えよう。すなわち

$$
\frac{\partial c(x,t)}{\partial t}=-kc(x,t)+D\frac{\partial^2 c(x,t)}{\partial x^2}
$$

という発展方程式を考える。同様に定常状態$${\frac{\partial c}{\partial t}=0}$$を考えることにする。境界条件を

$$
c(0,t)=c_{max}
$$

$$
c(\infty,t)=0
$$

とすると、解は

$$
c(x)=c_{max}exp(-\frac{x}{\lambda})
$$

であることは比較的容易に計算できる。すなわち、定常状態では指数関数的な勾配を示す。このモデルは先ほどと異なり系のサイズに依存せず、代わりに$${\lambda}$$によって特徴付けられている。このような指数関数的な濃度勾配はショウジョウバエのBicoidタンパク質などで有名であり、摂動に対して強いことが知られている。

次の節では、今述べた２つの条件における発展方程式を数値解析的に解いて、解析解とおおむね一致するかどうかを確認してみよう。

簡単な発展方程式の数値解析例

はじめに、どちらのシミュレーションも$${x=0,1,2,…,19}$$の20の地点における、１種類のモルフォゲンの濃度の系時的な変化を計算し、その推移を可視化することを目的としている、ということに注意してほしい。

まずは$${x=0}$$におけるモルフォゲン濃度が常に一定に保たれている場合について計算する。コードは以下の通り。

#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt

#各パラメーターの設定
dx=0.05
dt=0.1
Du=0.01

#初期条件とx=0での物質濃度の一定化
u0=np.linspace(0,0,20)
u0[0]=1
up=np.linspace(0,0,20)
up[0]=1

#拡散項
def left(u):
    x1=np.roll(u,1)
    x1[0]=x1[1]
    return x1
def right(u):
    x2=np.roll(u,-1)
    x2[19]=x2[18]
    return x2
def diffusion(u):
    ans=Du*(left(u)+right(u)-2*u)/dx/dx
    return ans
def dudt(u):
    ans=u+dt*(up+diffusion(u))
    return ans

#位置と時間軸
x0=np.linspace(0,19,20)
x1=np.linspace(0,999,1000)

#計算結果を行列yに代入
y=np.zeros((1000,20))
for s in range(1000):
        u0[0]=1
        u0[19]=0
        y[s,:]=u0
        u0=dudt(u0)

#可視化
xx0,xx1=np.meshgrid(x0,x1)
plt.figure(figsize=(15,15))
ax=plt.subplot(projection="3d")
ax.plot_surface(
    xx0,
    xx1,
    y,
    rstride=10,
    cstride=1,
    alpha=0.3,
    color="blue",
    edgecolor="black",
)
ax.set_zticks((0,1))
ax.view_init(35,-95)
plt.show()

これを実行することで得られるグラフはこちら。

次に、$${x=0}$$におけるモルフォゲン濃度が常に一定に保たれている条件下で、各地点で濃度に比例してモルフォゲンが各地点で分解される場合を考える。

#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt

#各パラメーターの設定
dx=0.05
dt=0.1
deg=0.5
Du=0.01

#初期条件とx=0での物質濃度の一定化
u0=np.linspace(0,0,20)
up=np.linspace(0,0,20)
up[0]=1

#拡散項
def left(u):
    x1=np.roll(u,1)
    x1[0]=x1[1]
    return x1
def right(u):
    x2=np.roll(u,-1)
    x2[19]=x2[18]
    return x2
def diffusion(u):
    ans=Du*(left(u)+right(u)-2*u)/dx/dx
    return ans
def dudt(u):
    ans=u+dt*(up-deg*u+diffusion(u))
    return ans

#位置と時間軸
x0=np.linspace(0,19,20)
x1=np.linspace(0,999,1000)

#計算結果を行列yに代入
y=np.zeros((1000,20))
for s in range(1000):
        y[s,:]=u0
        u0=dudt(u0)

#可視化
xx0,xx1=np.meshgrid(x0,x1)
plt.figure(figsize=(15,15))
ax=plt.subplot(projection="3d")
ax.plot_surface(
    xx0,
    xx1,
    y,
    rstride=10,
    cstride=1,
    alpha=0.3,
    color="blue",
    edgecolor="black",
    cmap='brg',
)
ax.set_zticks((0,1))
ax.view_init(15,-55)
plt.show()

これを実行することで得られるグラフはこちら。

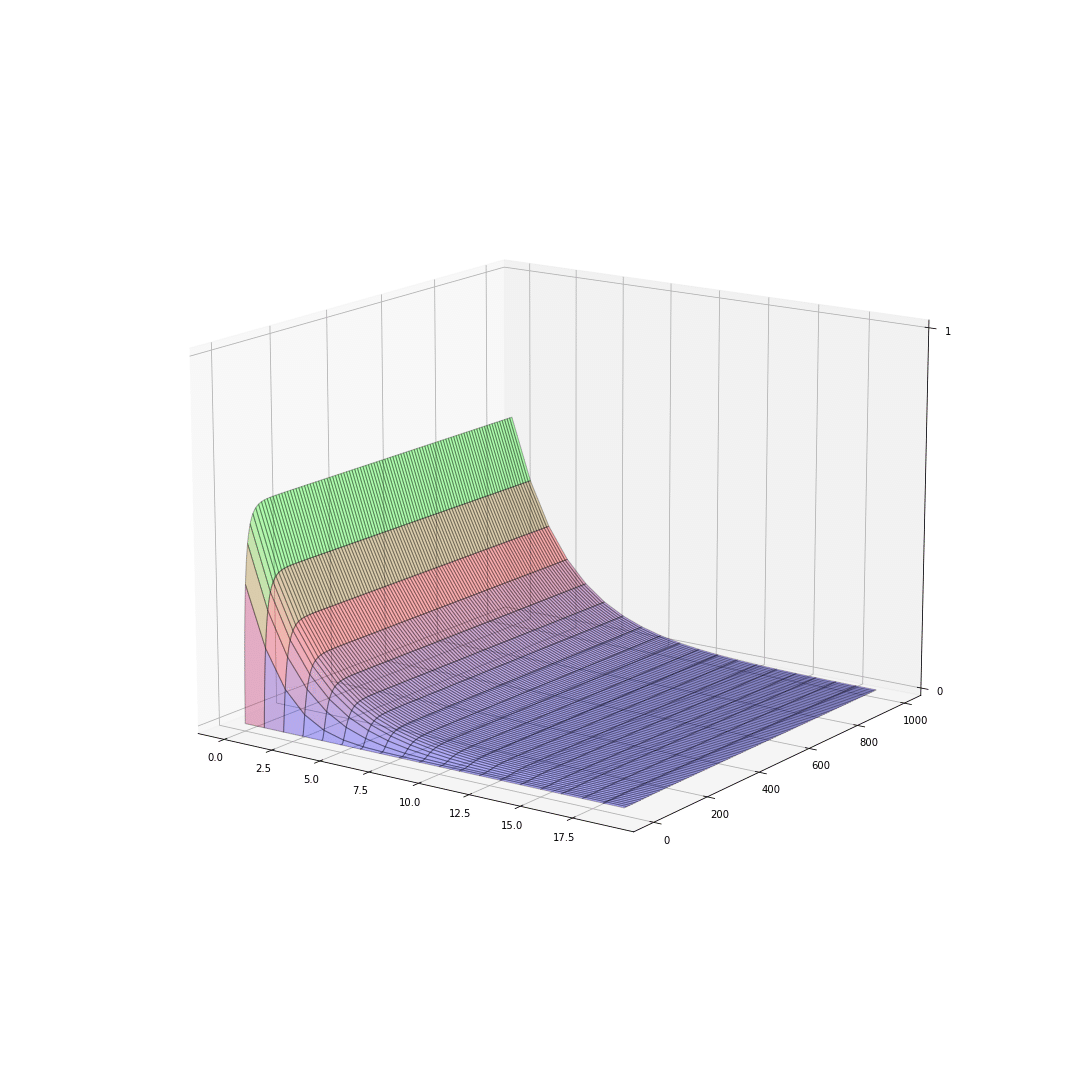
この条件下では、定常状態で位置に応じて**指数関数的な**勾配が形成されることがわかる。

以上により、（当然であるが）どちらの場合も数値解析解が解析解による結果とよく一致していることが確認できた。

さて、これまで考えてきたモデルでは、特定のモルフォゲンが、限定的な境界条件において局所的に湧き出す際に生じる勾配を考察してきた。これらはフィードフォワード的なシステムであり、もちろんそれだけでも、ある程度のパターン（縞模様など）を形成することが可能であることが知られている（例えばショウジョウバエの体節形成などは今のようなモデルの延長上として考えることができる）。ただし、より多様で頑健性に富んだ組織形成には、もう少し複雑な分子的実体が存在していて欲しい。例えば、空間のあらゆる場所で生成と分解が繰り広げられるような系では、一様解が不安定化し、周期的なパターン形成が出現する場合がある、ということがよく知られている。
これは、序盤に述べた組織形成の２つの誘導要因、すなわちモルフォゲンの濃度勾配と遺伝子制御ネットワークによる影響反映していると言える。要するに今までは、モルフォゲンの濃度勾配のみに着目して議論してきたが、それぞれの細胞がさまざまな種類の分子の入力を受け、内部で遺伝子発現を促進もしくは抑制し合うことによって、その細胞自身もまた出力を行っていると考えられるわけである。このような系を一般に反応拡散系と呼び、今回のモデルでは反応項が細胞内の遺伝子発現、拡散項がモルフォゲンの組織上での濃度勾配の時間発展に対応していると解釈できる。

反応拡散系（１次元）

反応拡散系は歴史的にはAlan Turingによって1952年に提唱された。ゆえに反応拡散系において特徴的に見られる周期的なパターンはTuring Patternと呼ばれる。Turing Patternの基盤となる数式自体は比較的シンプルであるにもかかわらず、自己組織化を説明する上で非常に強力であるがゆえに、これまで理論生物学においては非常に重宝されてきた（いる）。

まずは１次元空間における反応拡散系の時間発展について考えよう。
分子pと分子qという２種類のモルフォゲンを導入し、各細胞内におけるそれらの相互作用を

$$
\frac{dp}{dt}=f(p,q)=0.6p-q-p^3
$$

$$
\frac{dq}{dt}=g(p,q)=1.5p-2q
$$

という反応方程式で仮定する。したがって反応拡散方程式は

$$
\frac{\partial p}{\partial t}=f(p,q)+D_p\frac{\partial^2 p}{\partial x^2}
$$

$$
\frac{\partial q}{\partial t}=q(p,q)+D_q\frac{\partial^2 q}{\partial x^2}
$$

とかける（$${D_p}$$$${D_q}$$は各分子の拡散係数）。これをPythonを用いて数値解析してみよう。
コードは以下の通り。

#ライブラリのインポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

#パラメーターの設定
dx=0.02
dt=0.01

#初期条件を乱数で設定
np.random.seed(seed=1)
p=0.01*np.random.rand(50)
np.random.seed(seed=2)
q=0.01*np.random.rand(50)

#反応項
def f(p,q):
    ans1=0.6*p-q-p*p*p
    return ans1
def q(p,q):
    ans2=1.5*p-2*q
    return ans2

#拡散項
def diffusion(x):
    ans3=np.roll(x,1)+np.roll(x,-1)-2*x
    return ans3
def diffusionP(x):
    ans4=dp*diffusion(x)/dx/dx
    return ans4
def diffusionQ(x):
    ans5=dq*diffusion(x)/dx/dx
    return ans5
dp=0.0002
dq=0.01

#行列p、qを計算
def pAfterDt(p,q):
    ans6=p+dt*(f(p,q)+diffusionP(p))
    return ans6
def qAfterDt(p,q):
    ans7=q+dt*(q(p,q)+diffusionQ(q))
    return ans7
for i in range(5000):
    p=pAfterDt(p,q)
    q=qAfterDt(p,q)

#可視化
plt.plot(range(50),p, label="p")
plt.plot(range(50),q, label="q")
plt.xlabel("x")
plt.ylabel("concentration")
plt.legend()
plt.savefig("reaction_diffusion_one_dimension.png")
plt.show()

これを実行することで下図を得る。先ほどまでのモデルでは現れなかったような、周期的な濃度勾配が出現していることに注目してほしい。
この結果を定性的に説明してみよう。
発展方程式をよく見ると、分子pの合成はp自身により促進され、分子qにより抑制される。またpの濃度が高すぎる場合には強く抑制される。一方で分子qの合成は分子pにより促進され、q自身によって抑制される。また分子pとqの拡散係数の違いも重要である。今回のモデルでは分子qの拡散係数を分子pのそれよりもかなり大きく設定した。すなわち、分子pは局所的に作用して、一旦ある地点での濃度が高くなると自己触媒的に濃度が一気に上昇する。分子qはpの上昇に応じて合成されるが、急速に拡散するため、pのピーク周辺でpの合成を抑制する方向に働く。このようにして先ほどのパターンが形成されるのである。後ほど、これに関して定量的な解釈を行う。

反応拡散系（２次元）

二次元空間上に議論を拡大しよう。
反応方程式は先ほどと同じであるが、１つの細胞が上下左右の四方向から入力を受けるという点が異なる。
コードは以下の通り。

#ライブラリのインポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

#パラメーターの設定
dx=0.04
dt=0.02
dp=0.0002
dq=0.01


#初期条件を乱数で設定
np.random.seed(seed=1)
p=0.01*np.random.rand(50,50,1)
np.random.seed(seed=2)
q=0.01*np.random.rand(50,50,1)

#反応項
def f(a,b):
    return 0.6*a-b-a*a*a
def g(a,b):
    return 1.5*a-2.0*b

#拡散項
def diffusion(x):
    delta_diffusion=np.roll(x,1,axis=0)+np.roll(x,-1,axis=0)+np.roll(x,1,axis=1)+np.roll(x,-1,axis=1)-4*x
    return delta_diffusion/(dx*dx)

#計算
for i in range(2000):
    next_p=p[:,:,-1]+dt*(f(p[:,:,-1],q[:,:,-1])+dp*diffusion(p[:,:,-1]))
    next_q=q[:,:,-1]+dt*(g(p[:,:,-1],q[:,:,-1])+dq*diffusion(q[:,:,-1]))
    p=np.dstack([p,next_p])
    q=np.dstack([q,next_q])
    
#可視化
%matplotlib nbagg
from matplotlib.animation import PillowWriter,FuncAnimation
def animate(i):
    clock=dt*i*10
    step=i*10
    plt.cla()
    plt.imshow(p[:,:,i*10],interpolation='nearest',vmin=-1,vmax=1,cmap='jet')
    plt.title("t={0:.1f} ,step={1:3d}".format(clock,step))
fig=plt.figure()
plt.colorbar(plt.imshow(p[:,:,-1],interpolation='nearest',vmin=-1,vmax=1,cmap='jet'))
anim=FuncAnimation(fig,animate,repeat=False,frames=200,interval=10)
plt.show()

これはぜひGoogle Colaboratoryなどで実行してもらいたい。下の図のような模様が徐々に浮き上がってくる様が見られるであろう。ちなみに、初期条件として設定した乱数のseed値を指定していないため、実行するたびに結果は微妙に異なる点にも注目していただきたい。

２次元の反応拡散系の例
こちらの記事を大いに参考にさせていただきました。（https://qiita.com/STInverSpinel/items/595af7aa226907afd521）

発生において、今見てきたような繰り返しパターンは、体節や手足の骨、魚類の体表の模様など、さまざまな場所で見つけることができる。実際、生物においてTuring Patternが本当に出現しているかどうかは確証に至ってはいないものの、さまざまな観察や実験においてTuring Patternを裏付けるような報告が上がっている。

Turing 不安定性

この節は、力学系に関する前提知識を必要とするため、あまり馴染みのない方は読み飛ばしてもらって構わない。

これまでの多変数の反応拡散方程式は一般化すると

$$
\frac{\partial c_i(x,t)}{\partial t}=f_i(\textbf{c})+D_i \frac{\partial^2 c_i(x,t)}{\partial x^2}
$$

と表せる。
とりあえず、一旦拡散項を無視しよう。
その場合、固定点は

$$
\frac{\partial c_i(x,t)}{\partial t}=0
$$

を満たすような$${c_i(x,t)}$$の組み合わせ$${\textbf{c}^*}$$である。この固定点におけるヤコビアンを$${J}$$とすると、この系の線形安定性は$${J}$$の固有値$${\lambda}$$によって決定されるのであった（力学系理論の知識）。

ではこの解が、$${J}$$の固有値の実成分が全て負という条件の下（安定解）で、拡散項の影響により不安定になるかどうかを調べよう。

ここで、簡単のために、固有点の近傍における$${c_i(x,t)}$$が

$$
c_i(x,t)=c_i^*+C_i(t)sin(kx)
$$

とかけると仮定する（厳密にはフーリエ変換などを駆使する必要があるが、今回は単純化した。ただし、モチベーションは同じである）。
これを先ほどの式に代入することにより

$$
\frac{\partial C_i}{\partial t}=-D_i k^2 C_i +\Sigma_{j=1}^N J_{ij} C_j=\frac{\partial C_i}{\partial t}=\Sigma_{j=1}^{N} (J_{ij}-D_ik^2 \delta_{ij})\delta C_j
$$

を得る。したがって

$$
M_{ij}=J_{ij}-D_ik^2 \delta_{ij}
$$

とおけば、$${M}$$を拡散項がない場合における$${J}$$と同等の扱いをすればよいことがわかる。
よって行列$${M_{ij}}$$の固有値を$${{\lambda}_{i}(k)}$$とおけば、すべての$${i}$$についてその実部が負であれば、$${\textbf{c}^*}$$は安定である。逆に１つでも正のものがあれば不安定である。また実部が0のときは、定常的な空間的周期パターンが出現し、これこそがTuring 不安定性と呼ばれるものの正体である。

わかりやすいように、$${N=2}$$として、考えてみよう。
$${M_{ij}}$$の固有値は２次方程式

$$
\lambda^2-(J_{11}-D_1 k^2 + J_{22}-D_2 k^2)\lambda+ (J_{11}-D_1 k^2)(J_{22}-D_2 k^2) - J_{12}J_{21}=0
$$

の解である。２つの固有値の実部が負になる条件は、解と係数の関係により

$$
J_{11}+J_{22}<(D_1+D_2) k^2
$$

$$
J_{12}J_{21}<(J_{11}-D_1 k^2)(J_{22}-D_2 k^2)
$$

である。
したがって、拡散項がないとき（つまり$${k=0}$$のとき）に、この系が固有点近傍で線形安定となるのは、$${J_{11}>0}$$、$${J_{12}>0}$$の場合は$${J_{22}<0}$$、$${J_{21}<0}$$のときであり、$${J_{11}>0}$$、$${J_{21}>0}$$の場合は$${J_{22}<0}$$、$${J_{12}<0}$$のときである。前者のような系を基質消費系、後者のような系をアクティベータ・インヒビター系と呼ぶ。

また先ほどの式から、拡散項が追加されたときに、この安定性が崩れやすくなる条件は

$$
D_2\gg D_1
$$

であることがわかる。これは前節までで仮定した分子p、qの拡散係数の関係と同じであり、ゆえにTuring 不安定性が出現し、独特なパターンが形成されたことも理論的に説明できた。

細胞分化の数理

さて、ここまでで既に1.4万字を越してしまった。本来はここからがミソとなる予定だったのだが、時間がないので（実現するかどうかはわからないが）次回予告として、導入部だけを紹介したいと思う。

細胞分化の力学系モデル

ここからの話題は次の３つの論文を元にしている。興味のある方はぜひ読んでいただきたい。

https://www.science.org/doi/full/10.1126/science.1224311

https://www.science.org/doi/10.1126/science.aar4362

細胞分化に関する非常に有名なメタファーとして、WaddingtonのEpigenetic landscapeというものがある。これは上流に位置する幹細胞が、時間経過とともに下流の各細胞種へと分化し、その流れが不可逆的であることをよく表している。

細胞分化の分子生物学的な基盤はエピゲノム制御である。当然のことであるが、我々の体を構成する全細胞は（ほぼ）同じDNAを共有している。それでも多種多様な細胞が生まれてくるのは、共有しているDNAのどこを「読む」か、という違いに起因する。この巧妙な調節を行うのが、主にエピゲノム制御であり、ヒストン修飾やDNAメチル化が代表的である。

このエピゲノム変化は一般的に、外来因子の感知を起点として、細胞内のさまざまな種類のシグナルカスケードを経て、最終的には転写因子による発現調節によって達成される。やはり、ここでも遺伝子制御ネットワークが重要であり、幹細胞から一度分化した細胞は、その細胞種に特徴的な遺伝子群においてポジティブフィードバックループを形成することによって、安定化すると考えることができる。

細胞分化を数理的に捉える際には、力学系理論が有効であると言える。なぜならば、それぞれの細胞内には非常に多くの種類の遺伝子、 mRNA、タンパク質、各種キナーゼ、その他の代謝物などが存在しており、これは細胞ごとに異なる。すなわち、１つ１つの細胞は、それらの分子の発現量が織りなす高次元空間上の１つの点として捉えることができる。これはまさに力学系理論における相空間の考え方である。また、１つ１つの細胞は無秩序に高次元空間上に位置しているわけではなく、似たような表現型を示す細胞群は近い位置に集まる。つまり、数多もの種類の生体分子が織りなす高次元空間上において、細胞が集まりやすい領域（細胞分化の果てに収束しやすい領域と言い換えても良い）が存在し、これが分化後の細胞種、１つ１つに対応すると捉えることができる。この「集まりやすい領域」のことを力学系理論の言葉ではアトラクターと呼ぶ。
以上を簡単にまとめると、１つの細胞はその細胞内の遺伝子やmRNA、タンパク質などの構成要素の発現量によって、高次元空間上の１つの点として表現でき、細胞分化とは、細胞内や細胞間の相互作用の結果として、幹細胞の状態から複数存在するアトラクターの１つへ不可逆的に遷移すること、と捉えることができる。

細胞分化の力学系モデル
（Chikara Furusawa, Kunihiko Kaneko, A Dynamical-Systems View of Stem Cell Biology.Science338,215-217(2012).より引用）

シングルセルトランスクリプトーム解析による細胞分化の可視化

2018年、受精後様々な時刻のゼブラフィッシュ胚の細胞でシングルセルのトランスクリプトーム解析を行い、その発現量データをt-SNEという次元圧縮手法を利用して、細胞分化の時間変化を可視化した、という非常に興味深い論文がScienceに掲載された（参考文献7）。

t-SNEによる細胞分化の可視化
（Wagner DE, Weinreb C, Collins ZM, Briggs JA, Megason SG, Klein AM. Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science. 2018 Jun 1;360(6392):981-987. doi: 10.1126/science.aar4362. Epub 2018 Apr 26. PMID: 29700229; PMCID: PMC6083445.より引用）
この記事のヘッダーはこの図です。

先ほどの細胞種の高次元相空間モデルのみならず、生物学の研究全般に言えることだが、（雑に言えば）生命体はとにかく複雑なのだ。細胞１つを取ってもその構成要素は膨大である。
ゆえに2010年代以前の生命科学の基礎研究は、仮説駆動型の分子生物学的なアプローチによって、「特定の遺伝子を欠損させた場合にはこういうことが起こる」、「分子Aは分子Bをリン酸化する」など、局所的かつ断片的な知識の収集という面が強かった。しかし近年の技術発展と解析手法の浸透化によって、データ駆動型のアプローチも急速に増加している。
この論文は、そのような時代の流れの中で、我々人間には直感的に認識できない高次元空間上における各細胞の状態を、ある程度認識可能な表現に落とし込んだという点で象徴的とも言えよう。

細胞分化を可能にするネットワーク構造

2011年、細胞内に５つの遺伝子とそのタンパク質を仮定し、それらが構成しうる全ての遺伝子制御ネットワークにおいて、細胞間相互作用や細胞分裂も考慮した上で、それぞれの細胞内のタンパク質発現量の変化から細胞分化を説明するモデルに関する論文が発表された。
元々はこの記事の中で、その論文のアルゴリズムを実装する予定であったが、アドカレの掲載が遅れてしまいそうなので、今回は見送る。もしかしたら続編を書くかもしれないので、その際には実装してみよう。
その論文では、そうした数値シミュレーションの結果、細胞分化現象を再現するような遺伝子制御ネットワークをスクリーニングした上で、それらに共通するネットワークモチーフを考察した。さらに、その結果から逆に階層的な細胞分化を誘導するような遺伝子制御ネットワークを設計し、数値シミュレーションでその実現を確認したのである。

参考文献

『細胞の理論生物学』
『発生の数理』
『ギルバート発生生物学』
Suzuki N, Furusawa C, Kaneko K. Oscillatory protein expression dynamics endows stem cells with robust differentiation potential. PLoS One. 2011;6(11):e27232. doi: 10.1371/journal.pone.0027232. Epub 2011 Nov 3. PMID: 22073296; PMCID: PMC3207845.
Kicheva A, Briscoe J. Control of Tissue Development by Morphogens. Annu Rev Cell Dev Biol. 2023 Oct 16;39:91-121. doi: 10.1146/annurev-cellbio-020823-011522. Epub 2023 Jul 7. PMID: 37418774.
Chikara Furusawa, Kunihiko Kaneko, A Dynamical-Systems View of Stem Cell Biology.Science338,215-217(2012).
Wagner DE, Weinreb C, Collins ZM, Briggs JA, Megason SG, Klein AM. Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science. 2018 Jun 1;360(6392):981-987. doi: 10.1126/science.aar4362. Epub 2018 Apr 26. PMID: 29700229; PMCID: PMC6083445.
https://qiita.com/STInverSpinel/items/595af7aa226907afd521
https://www.se.fukuoka-u.ac.jp/iwayama/teach/kisoIII/text_3.pdf

~~ここまで読んでくれている方がいるとは正直全く想定していないですが、~~読んでいただきありがとうございました。
また時間がある時にでも、第２弾を執筆できたらいいなと密かに思っています。

この記事が気に入ったらサポートをしてみませんか？