
モンティ・ホール問題と条件付き確率
筆者が初めてモンティ・ホール問題を知ったのは中学生くらいの頃だったかと思う。その時点で既にモンティ・ホール問題という記事がWikipediaにあって、筆者は当時その説明に納得できなかった記憶がある。
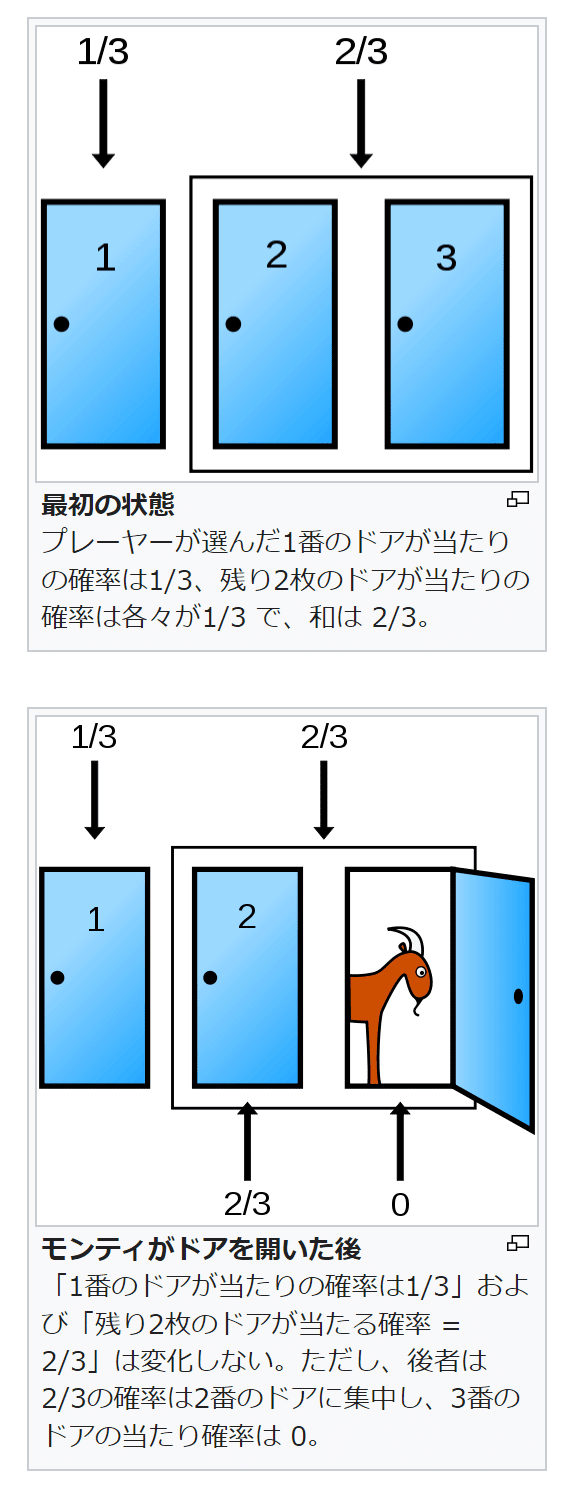
筆者が特に納得できなかったのは<「1番のドアが当たりの確率は1/3」および「残り2枚のドアが当たる確率は2/3」は変化しない。ただし、後者は2/3の確率は2番のドアに集中し、3番のドアの当たり確率は0である>といったような内容の箇所であった。
<「1番のドアが当たりの確率」=「2番のドアが当たりの確率」=「3番のドアが当たりの確率」=1/3>というのは当時の筆者にも容易に理解できた。
しかし、<「1番のドアが当たりの確率は1/3」および「残り2枚のドアが当たる確率は2/3」はドアが開いた後も変化しない>という箇所に対しては、ご都合主義のようなものを当時の筆者は感じてしまったのだった。
当時の筆者が感じてしまっていたことを以下にまとめる。
Wikipediaの図解では、「1番のドアが当たりの確率」と「2番もしくは3番のドアが当たりの確率」とを分けている。このように分けてよいのなら、「1番もしくは2番のドアが当たりの確率」と「3番のドアが当たりの確率」とを分けて考えても良いということになるのではないか?
Wikipediaの図解に倣うならば、3番のドアが開いた後も、「1番のドアが当たりの確率」と「2番のドアが当たりの確率」の和は2/3のままであり、「3番のドアが当たりの確率」は1/3のままとなるはずである。
しかし、「3番のドアが当たりの確率」が1/3のままであることと、3番のドアが開かれたことで「3番のドアが当たりの確率」が0となったことは矛盾する。
Wikipediaの図解では、「1番のドアが当たりの確率」と「2番もしくは3番のドアが当たりの確率」とを分けている。このように分けてよいのなら、「1番もしくは3番のドアが当たりの確率」と「2番のドアが当たりの確率」とを分けて考えても良いということになるのではないか?
Wikipediaの図解に倣うならば、3番のドアが開いた後も、「1番のドアが当たりの確率」と「3番のドアが当たりの確率」の和は2/3のままであり、「2番のドアが当たりの確率」は1/3のままとなるはずである。
すると、今度は「1番のドアが当たりの確率」が1/3から2/3に倍増することとなる。
「1番のドアが当たりの確率」と「2番もしくは3番のドアが当たりの確率」とを分けているWikipediaの図解はご都合主義のような胡散臭さを感じてしまう。
当時の筆者がWikipediaの図解をご都合主義のように感じてしまった最大の理由はモンティ・ホール問題のルールを正確に把握していなかったことが挙げられる。
モンティ・ホール問題のルールをWikipediaの文章を参考にしながら列挙していくこととする。
(1) 3つのドアのうち1つだけに当たりが入っており、残り2つは外れである。3つのうちどれに当たりが入っているかは完全にランダムである。モンティは3つのうちどれに当たりが入っているのかを知っている。
(2) プレーヤーはドアを1つ選ぶ。
(3) モンティはプレイヤーが選ばなかった残りの2つのドアから1つを必ず開ける。モンティの開けるドアは外れの入っているドアであり、モンティが当たりの入っているドアを開けることは絶対にない。仮にプレーヤーが(2)で当たりの入っているドアを選んでいた場合、モンティが残るドアのどちらを開けるのかは完全にランダムである。
(4) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。
(3)において「プレイヤーが選ばなかった残りの2つのドア」が太字となっている。この太字の箇所は「プレイヤーが選んだドアをモンティが開くことは、プレイヤーが選んだドアが当たりであるか外れであるかによらず、絶対にないということ」を意味している。
仮にプレーヤーが(2)で外れを選んでいた場合、「プレイヤーが選ばなかった残りの2つのドア」は、当たりのドア1つと外れのドア1つから構成されていることとなる。モンティの開けるドアは、「プレイヤーが選ばなかった残りの2つのドア」のうち、外れの入っている方のドアなので、仮にプレーヤーが(2)で外れを選んでいた場合、モンティは「プレイヤーが選ばなかった残りの2つのドア」のうち外れのドアを必ず開けることとなる。
つまり、仮にプレーヤーが(2)で外れを選んでいた場合、「プレイヤーが選ばなかった残りの2つのドア」のうちモンティが開かなかった方のドアは必ず当たりとなる。
当時の筆者が<「1番のドアが当たりの確率」と「2番もしくは3番のドアが当たりの確率」とを分けるのは良くて、「1番もしくは3番のドアが当たりの確率」と「2番のドアが当たりの確率」とを分けたり、「1番もしくは3番のドアが当たりの確率」と「2番のドアが当たりの確率」とを分けたりするのはダメというのはご都合主義みたいだ>と感じてしまったのは、「プレイヤーが選んだドアをモンティが開くことは、プレイヤーが選んだドアが当たりであるか外れであるかによらず、絶対にないというルール」を正確に把握できていなかったためである。
筆者が初めてモンティ・ホール問題を知って半年か数年かが経ったころ、学校の数学の授業で条件付き確率というものを学んだ。
モンティ・ホール問題の解法は複数あり、Wikipediaの図解のように「1番のドアが当たりの確率」と「2番もしくは3番のドアが当たりの確率」とを分けて考える解法のほか、条件付き確率で考える解法もある。
だが、条件付き確率という概念は慣れていないと扱うのが中々難しいと思われる。
例題を考案してみたので解いてみてほしい。
問1:男児が生まれる確率と女児が生まれる確率が完全に同じであり、いちど生まれた子供は成人するまでは絶対に死なないと仮定する。或る夫婦に2人のお子さんがいて、あなたは昨日まで「その夫婦には2人のお子さんがいるということ」しか知らなった。
あなたは今日とある育児セミナーに参加した。すると、その夫婦もセミナーに参加しているのが分かった。セミナー講師が「男児がいるご家庭の方は手をあげて下さい」と言ったところ、その夫婦は手をあげていた。これを見てあなたは「この夫婦には長男がいるのだな」と分かった。このとき、長男でない方のお子さんも男児である確率を求めよ。
問2:男児が生まれる確率と女児が生まれる確率が完全に同じであり、いちど生まれた子供は成人するまでは絶対に死なないと仮定する。或る夫婦に2人のお子さんがいて、あなたは昨日まで「その夫婦には2人のお子さんがいるということ」しか知らなった。
あなたは今日とある育児セミナーに参加した。すると、その夫婦もセミナーに参加しているのが分かった。セミナー講師が「最も年上のお子さんが男児であるというご家庭の方は手をあげて下さい」と言ったところ、その夫婦は手をあげていた。これを見てあなたは「この夫婦には長男がいるのだな」と分かった。このとき、長男でない方のお子さんも男児である確率を求めよ。
※「もしも2人のお子さんが双子だとしたら年上や年下の区別ができないのではないだろうか」と不安に思う読者もいるかもしれない。しかし双子というケースを想定するにしても、「先に生まれた方の赤ん坊」を年上とし、「後に生まれた方の赤ん坊」を年下とすれば、年上や年下の区別は可能である。要するに本問題を考えるうえで、この2人が双子であるケースを考える必要はない。
条件付き確率に慣れていないと「問1も問2も1/2でしょ」などと判断してしまうかもしれない。しかし、この判断は実は誤りである。問2は1/2で合っているのだが、問1は1/3が正しい答えなのである。
以下に解説を載せる。
(年上の性別,年下の性別)は、(男,男), (男,女), (女,男), (女,女) の4通りであり、この4通りは同様に確からしい。
問1は「2人のお子さんのうち少なくとも1人が男児だ」という条件がついており、(2人とも男である確率)/(少なくとも1人が男である確率)を求めればよい。
(2人とも男である確率)を考える。
(男,男), (男,女), (女,男), (女,女) の4通りのうち、2人とも男であるのは(男,男)の1通り。
よって(2人とも男である確率)=1/4である。
(少なくとも1人が男である確率)を考える。
(男,男), (男,女), (女,男), (女,女) の4通りのうち、少なくとも1人が男であるのは(男,男), (男,女), (女,男)の3通り。
よって(少なくとも1人が男である確率)=3/4である。
(1/4) / (3/4)より、問1で求めるべき確率は1/3である。
問2は「2人のお子さんのうち年上のお子さんが男児だ」という条件がついており、(2人とも男である確率)/(年上が男である確率)を求めればよい。
(2人とも男である確率)を考える。
(男,男), (男,女), (女,男), (女,女) の4通りのうち、2人とも男であるのは(男,男)の1通り。
よって(2人とも男である確率)=1/4である。
(年上が男である確率)を考える。
(男,男), (男,女), (女,男), (女,女) の4通りのうち、年上が男であるのは(男,男), (男,女)の2通り。
よって(年上が男である確率)=2/4である。
(1/4) / (2/4)より、問2で求めるべき確率は1/2である。
類題として問3と問4も考案した。
問3:男児が生まれる確率と女児が生まれる確率が完全に同じであり、いちど生まれた子供は成人するまでは絶対に死なないと仮定する。或る夫婦に2人のお子さんがいて、あなたは昨日まで「その夫婦には2人のお子さんがいるということ」しか知らなった。
あなたは今日とある育児セミナーに参加した。すると、その夫婦もセミナーに参加しているのが分かった。セミナー講師が「男児がいるご家庭の方は手をあげて下さい」と言ったところ、その夫婦は手をあげていた。このとき、その夫婦の2人のお子さんが両方とも男児である確率を求めよ。
問4:男児が生まれる確率と女児が生まれる確率が完全に同じであり、いちど生まれた子供は成人するまでは絶対に死なないと仮定する。或る夫婦に2人のお子さんがいて、あなたは昨日まで「その夫婦には2人のお子さんがいるということ」しか知らなった。
あなたは今日とある育児セミナーに参加した。すると、その夫婦もセミナーに参加しているのが分かった。セミナー講師が「最も年上のお子さんが男児だというご家庭の方は手をあげて下さい」と言ったところ、その夫婦は手をあげていた。このとき、年下の子も男児である確率を求めよ。
条件付き確率を理解できていれば、「問3の正答は問1と同じく1/3であり、問4の正答は問2と同じく1/2である」ということが分かるかと思う。
モンティ・ホール問題を条件付き確率で考えてみよう。
プレイヤーは最初、1番のドアを選ぶ場合と2番のドアを選ぶ場合と3番のドアを選ぶ場合とがある。
ルール(1)より、「プレイヤーは最初、1番のドアを選ぶ」と仮定しても一般性は失われない。
「プレイヤーは最初、1番のドアを選ぶ」という仮定より、モンティは2番か3番かのどちらか一方のドアを必ず開くこととなる。
当たりが1番のドアにあり、モンティが1番のドアを開ける確率を P (当1開1) と表記することとする。なお、以下の確率はプレイヤーが最初に1番のドアを選んだ時点でのものである。
P (当1開1) = 0
P (当2開1) = 0
P (当3開1) = 0
P (当1開2) = (1/3) × (1/2) = 1/6
P (当2開2) = 0
P (当3開2) = 1/3
P (当1開3) = (1/3) × (1/2) = 1/6
P (当2開3) = 1/3
P (当3開3) = 0
「プレイヤーは最初、1番のドアを選ぶ」という仮定より、モンティは2番か3番かのどちらか一方のドアを必ず開くこととなる。
まずモンティが3番のドアを開くと仮定する。
(モンティが3番のドアを開いた後もプレイヤーがドアを変えなかった場合に当たりとなる確率)は「モンティが3番のドアを開いた」という条件が付いている。
よって
(プレイヤーがドアを変えなかった場合に当たりとなる確率)
=P (当1開3) / {P (当1開3) + P (当2開3) +P (当3開3)}
=1/3
(モンティが3番のドアを開いた後プレイヤーがドアを変えた場合に当たりとなる確率)は「モンティが3番のドアを開いた」という条件が付いている。
よって
(プレイヤーがドアを変えた場合に当たりとなる確率)
=P (当2開3) / {P (当1開3) + P (当2開3) + P (当3開3)}
=2/3
つぎにモンティが2番のドアを開くと仮定する。
(モンティが2番のドアを開いた後もプレイヤーがドアを変えなかった場合に当たりとなる確率)は「モンティが2番のドアを開いた」という条件が付いている。
よって
(プレイヤーがドアを変えなかった場合に当たりとなる確率)
=P (当1開2) / {P (当1開2) + P (当2開2) + P (当3開2)}
=1/3
(モンティが2番のドアを開いた後プレイヤーがドアを変えた場合に当たりとなる確率)は「モンティが2番のドアを開いた」という条件が付いている。
よって
(プレイヤーがドアを変えた場合に当たりとなる確率)
=P (当3開2) / {P (当1開2) + P (当2開2) + P (当3開2)}
=2/3
すなわち、モンティが2番のドアを開いたとしても、3番のドアを開いたとしても、プレイヤーがドアを変える場合、ドアを変えない場合と比べて当たりとなる確率が2倍となる。
モンティ・ホール問題の理解を難しくしている要因は主に二つあるかと思う。一つはルールを正確に把握できているかいないかという点である。もう一つは、「モンティがドアを一つ開けた後にドアを変えたときに当たりとなる確率」と「モンティがドアを一つ開けた後にドアを変えなかったときに当たりとなる確率」が条件付き確率となっている点である。
モンティ・ホール問題の解法には、Wikipediaの図解のように「1番のドアが当たりの確率」と「2番もしくは3番のドアが当たりの確率」とを分けて考える解法や、条件付き確率で考える解法などがあるが、筆者は条件付き確率で考える解法を強く推奨したい。
もちろん、条件付き確率という概念自体を知らない人の場合は、条件付き確率自体を学ぶ必要が生じる訳だが、それでも条件付き確率で考える解法には、モンティ・ホール問題以外にも応用が利くという大きなメリットがある。
最後になるが、モンティ・ホール問題を知らない人に、この問題を紹介するときは、「前述したモンティ・ホール問題のルール (1) ~ (4) 」を丁寧に伝えておく必要があるように思う。
※本記事もしくは本記事の内容と関連する漫画を何らかのかたちで発表する予定。いつごろ発表するかは未定。
この記事が気に入ったらサポートをしてみませんか?
