
第16回 情報源符号化 その5(ハフマン符号)
阿坂先生
前回作成した符号は実は無駄がある符号なのじゃ。まず、それを確認してから無駄のないハフマン符号を見て行こう。
桂香助教
まず前回作った符号は以下だったわね。

この符号の符号の木を書いてみて!
麦わら君
書いてみました。こんな感じですか?確かに無駄に長いところがある気がします。

桂香助教
そうよ。青色で示した枝はカットしても語頭条件を守られた符号になるわ。
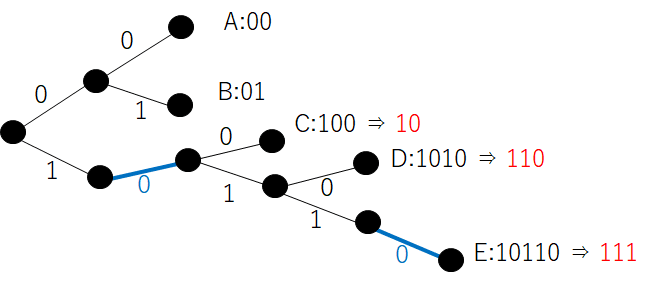
青の枝を取り除くと赤の符号語になって符号語長が短くなっているのがわかるわよね。語頭条件も満たされている。
阿坂先生
平均符号語長を短くするために無駄なく符号語を作りたい。上の図のように無駄な部分をなくした符号のことを最小冗長符号又はコンパクト符号というぞぃ。
桂香助教
これから勉強するハフマン符号は最小冗長符号よ。
麦わら君
ハフマン符号は良い符号なんですね。でも、そんな性能の良い符号は符号化するのはかなり複雑なんじゃないですか?
阿坂先生
ふふふ。ハフマン符号の符号化は難しくないぞぃ。とても便利な符号化方式だからぜひ覚えて欲しい。ではやり方を説明するぞぃ。
① 出現確率が最も小さい記号とその次に小さい記号を1つにまとめる符号の木を作成する。
② 上記の2つの記号の出現確率を足し合わせて新たな出現確率を計算する。
③ 新たな出現確率も含めて、木が完成するまで①と②を繰り返す。
④ 符号の木のすべての枝に「0」と「1」を割り当てる。
⑤ 符号の木の根から葉までの各枝に割り当てられた0と1を順番に並べたものが葉に割り当てられる符号語になる。
桂香助教
では最初に挙げた表の記号をハフマン符号で符号化してみるわ。

①の「出現確率が最も小さい記号とその次に小さい記号を1つにまとめる符号の木を作成する」だけど、出現確率が最も小さいのはDでその次に小さいのがAなのでこれをまとめた符号の木は以下だわ。

そして、「②上記の2つの記号の出現確率を足し合わせて新たな出現確率を計算する」なのでAとDの出現確率を足すと0.15となり新たな出現確率は以下よ。

次に③ね。今度は0.35、0.3、0.2、0.15の中で最も出現確率が低いものと2番目に低いものを探すのよ。これが①に戻った作業。この例では0.2と0.15になるわね。これを新しい確率0.35も計算して符号の木を描いたのが以下よ。

この作業を繰り返す。次はEとBね。

最後は木を完成させて

となるわね。次は④よ。枝に0と1を割り当てて行くんだけど、適当に割り振るんじゃなくて上の枝は0、下の枝は1というふうにどちらかに決めて割り振ってね。上の枝を0、下の枝を1と割り振った符号の木は以下よ。

そして、⑤よ。根から順番に0と1を割り当てて行くよの。Eだと枝は00ね。Aは110ね。表にまとめると以下よ。

木の構造で内部頂点に符号語がないので語頭条件は満足している。平均符号語長Lを計算してみると2.15になるわ。前回、エントロピーHは2.06と計算したわ。今回、ハフマン符号で符号化したLはHにかなり近い値になっているわ。
阿坂先生
もっと近づけるためには拡大情報源を使えば良いのじゃ。これは前回説明したことじゃ。
麦わら君
ちょっと気になることがあるんですが。(※)の図でEとBを1つのまとめていたんですが、CADをまとめたものも確率0.35でEと同じなので、BとCADの組み合わせじゃダメですか?
阿坂先生
よいところに気がついたのぉ。それでもOKじゃ。こうやって符号化しても同じ平均符号語長になる。実際にやってみよう。
桂香助教
以下がBとCADの組み合わせて描いた符号の木とできた符号語よ。


そして、平均符号語長Lは2.15になる。
麦わら君
おー同じになるんですね。このハフマン符号、符号化のやり方も難しくないし便利ですね。
阿坂先生
そうじゃ。このハフマン符号はFAXの符号化方式に応用されておる。
情報源符号化定理はここまでじゃ。だいぶ、長く情報源符号化定理を勉強してきたが一旦終わりとしよう。次回からは通信路符号化定理について勉強する。次は誤りなく伝送するための方式の勉強じゃ。
これから記事を増やしていく予定です。
