
【GTOはここから】AKQゲームって結局なんなのさ(後編)
※こちらの記事は後編です!先に前編を読んでからご覧ください!
▼前編はこちらから!
さて、簡単に前編の内容をまとめるとこんな感じです。
✔️AKQゲームではA/Q側(Pさん)とK側(Cさん)に分かれる
✔️PさんはAの全て(value)とQを頻度(bluff)でbetする
✔️CさんはKを頻度でcallする(bluff catch)
✔️お互いのbet/call頻度でEVは変化する
って感じですね。
前編ではQのbet頻度/Kのcall頻度をそれぞれ固定した際の
EVの変化をグラフにしながら確認してきました。
そして前編の最後にはPさん、Cさんがそれぞれbet/call頻度を変化させる場合も表にしました。こんな感じのやつですね。

今回はここからGTOの根幹にある"ナッシュ均衡"と
そこから発展して自身のEVを最大化する方法について考えていきます。
AKQゲームからナッシュ均衡を考える
さて、ポーカーをやってるとちょいちょい耳にする
"ナッシュ均衡"あるいは"均衡"という表現。これは一体何なのか。
困った時のWikipedia先生に聞いてみましょう。
ナッシュ均衡は、他のプレーヤーの戦略を所与とした場合、どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせである。ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない。
うーん、何のこっちゃですね。
これまでのAKQゲームで言い換えればこんな感じでしょうか。
自分のbet/call頻度を変えても自身のEVが変化しない状態
って感じですね。
あ、そういえば前編でこんなグラフがあったような…

Pさんがpot100%betをした際のQのbet頻度の変化に伴う
PさんのEVをグラフにしたものですね。
このグラフの黄色線を見て貰えば分かりますが、
Kのcall頻度が50%の場合に限っては、Qのbet頻度を変えてもPさんのEVが変わってないですよね。
これって先ほど述べた
自分のbet/call頻度を変えても自身のEVが変化しない状態
になっているわけです。
Pさん側はQのbet頻度をどう変化させても
EVを増加させられないわけです、悲しい🥺
これは逆のことも言えて、このグラフも同じです。

こちらでは、Qのbet頻度が50%の場合に限っては
Kのcall頻度を変えてもCさんのEVが変わってないですね。
これも同様に
自分のbet/call頻度を変えても自身のEVが変化しない状態
になっているわけです。
Cさん側はKのcall頻度をどう変化させても
EVを増加させられないわけです、これまた悲しい🥺
これを今度は先ほどのサーモグラフィーで考えてみます。
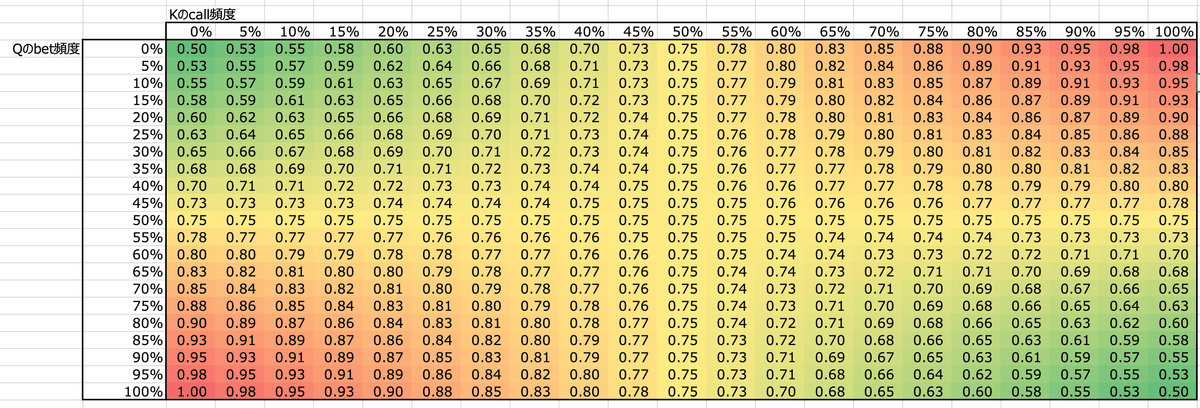
さらにコイツを分かりやすくするために少し手を加えます。

Qのbet頻度が50%の行、Kのcall頻度が50%の列(それぞれ太字になってる)だけはずっとEVが0.75で変化していないわけです。
そしてこの交点の赤字部分こそナッシュ均衡になるわけです。
さて、もう一度ナッシュ均衡の定義を見てみましょう。
ナッシュ均衡は、他のプレーヤーの戦略を所与とした場合、どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせである。ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない。
ここで説明を2つに分けます。
①どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせ
②ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない
ってところですね。
①どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせ
に関してはこれまで説明してきた通り、自分の戦略を変えても
PさんのEVは0.75、CさんのEVは0.25で変化しません。
次に
②ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない
についてです。
要は期待値の最大化の観点ではこのナッシュ均衡状態から
双方戦略を変更することはないよね、ってことなんですが
このグラフの赤字部分から数値を動かす、例えば
Cさんがcall頻度を50%から80%に変化させたとしましょう。

するとグラフ上ではこんな感じで移動します。
これまでの解説の通り、Cさんがcall頻度を80%にしたところで
Pさん、Cさん双方のEVは何も変化しません。
しかしここで重要なのは、こうなった場合Pさん側は次のような選択を取れることです。

そうなんです。いざCさんが80%でcallするとなれば、
Pさん側はQのbet頻度を0%にすることでEVを0.90まで増加させられます。
(その分CさんのEVは0.10に減少します)
つまり、Cさんはナッシュ均衡から戦略を変化させてしまったことで
自身がEVを減少させる要因を作ってしまったわけです。
これこそが
②ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない
なわけですね。
(ちなみにこのPさんの行った「Qのbet頻度を0%にする」というアクションこそがExploitそのものです)
ってことで改めてナッシュ均衡の定義とAKQゲームを関連させてまとめると
✔️ナッシュ均衡下では双方が戦略を変化させても自身のEVは増加せず、むしろ自身のEVが減少する余地を生んでしまう。
✔️AKQゲームにおいてはQのbet頻度、Kのcall頻度がとある点においてナッシュ均衡状態になる。
ってな話ですね。
そして、このナッシュ均衡をポーカーという複雑なゲームに落とし込んだ結果こそが、我々が普段GTO Wizardで目にしているものです。
もちろんポーカーではAKQゲームのような単純な状況ではないので
ここまでシンプルなものでもないですし、手計算できるようなものでもないです。
ただ、実際ほぼこのようなシチュエーションはあって
例えば以下のようなシチュエーション。
UTG r 2.3bb (eff.80bb)
BB c
Flop AK6r(6.1bb)
BB x/c
UTG b 6.1bb
Turn 2(18.3bb)
BB x/c
UTG b 15.2bb
River 4(48.7bb)
BB x/?
UTG AI 56.4bb
RiverでのUTGのAIはpotの116%です。
この時のUTGのAIのレンジ構成は以下の通り。

トップペア以上をvalueだとすれば、valueとbluffの比率はざっくり7:3ですね。
それに対するBBのcall頻度はレンジの45.5%です。
この値はこれまで計算してきたpot100% betのA/Q比率、Kのcall頻度に近い値になっています。
(厳密にはBBにも2ペア+があるので異なる部分はありますが)
ナッシュ均衡のままEVを大きくする方法があった!?
ここまでの議論を踏まえるとナッシュ均衡下ではそれ以上EVは大きくできないので、指を咥えてナッシュ均衡戦略に従っておいてくださいね、って話になっちゃいます。
「いや何とかしてもっとEVを大きくできないものか。。。」
そうだ!そういえばAKQゲームの別の変数をいじっちゃえばいいんじゃないのか!?
そうです。AKQゲームでの変数は以下の通り。
①PさんのAとQの構成比は?
②Pさんのbetサイズはどうする?
③PさんはQをどの頻度でbetする?
④CさんはKをどの頻度でcallする?
そして前編からここまでの議論では
①PさんのAとQの構成比→A:Q=50%:50%
②Pさんのbetサイズ→pot 100%のみ
と固定していたのでした。
ここをイジれば何とかなるのでは!?
ということで次はA/Qの構成比とbetサイズを変化させることを考えます。
※前提条件が変わった時点でナッシュ均衡の条件も変化するので、正確には「同一条件のゲームでのナッシュ均衡下でEVを増やせる」ということは起こり得ません。
※以降はPさんをpolar、Cさんをcondensedと表現します。
例えばAとQの含有率を50%/50%にしたまま
bet sizeだけ150%にしてみます。するとどうなるか。

こんな感じでbet sizeが100%だった場合と比べてナッシュ均衡における
Qのbet頻度やKのcall頻度が変わっています。
(Qのbet頻度が60%/Kのcall頻度が40%)
そして、最大のポイントはそのナッシュ均衡における
polar側のEVが0.8になっていることです。
(pot100%betでは0.75でした)
つまりbet sizeを100%から150%に変えたことで
polar側のEVが増加していることになります。
(その分condensed側のEVは低下してます)
━━━━━━━━━━━━━━
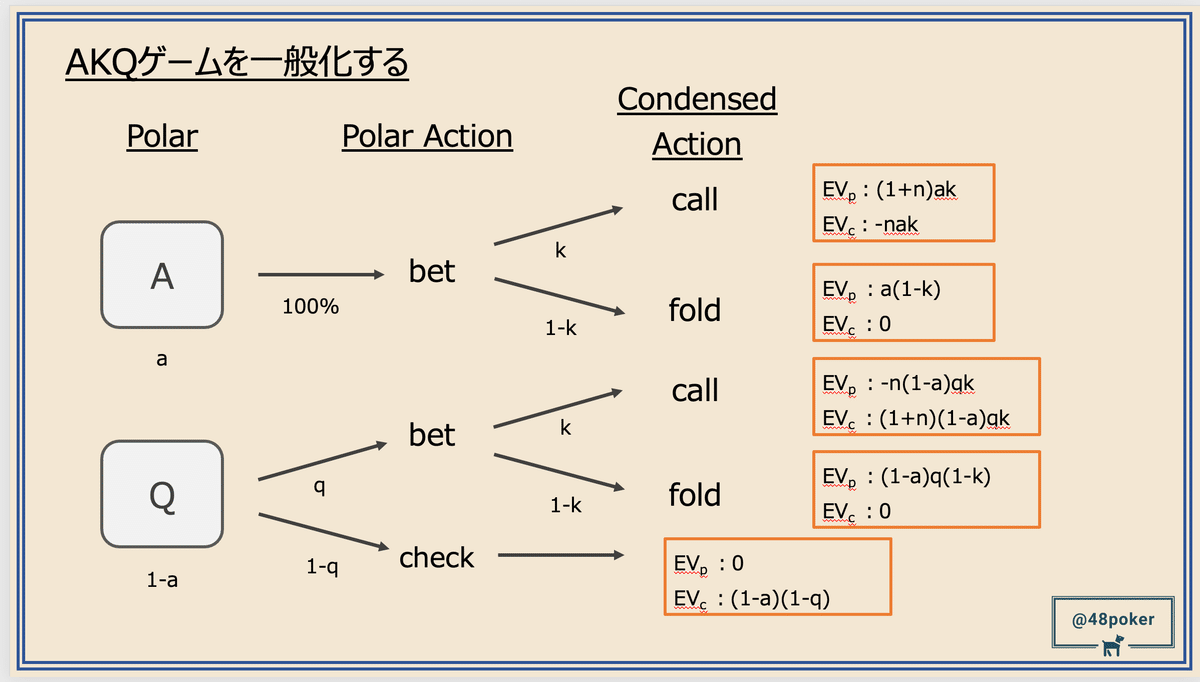
さて、ここからはより一般的に議論をするために
文字を置いて計算することにします。
ここからの議論は数学の授業みたいになります🥺
なるべく数学苦手な人でも分かりやすいように説明していくのでついてきていただければ!
まずは以下のように変数設定します。
Pot size:1
レンジ内のAとQの含有率:A:Q = a:1-a
Bet size:n(pot比)
Qのbet頻度:q
Kのcall頻度:k
なお、0<a<1、0≦q,k≦1、0<nとする。
一気にややこしくなった感じもしますが、
実は丁寧に場合分けしていけばそこまでEVの計算は難しくありません。
ってことで途中過程をすっ飛ばして計算結果を表記するとこんな感じです。
EVp= a+q+nak+akq+nakq-aq-kq-nkq
文字がごちゃごちゃ並んで何のこっちゃだと思いますが、
ふ〜んくらいに思っておいてください。笑
上記の式をそれぞれ下記のように括る。
①EVp = a+q-aq+k(na+aq+naq-q-nq)
②EVp = a+nak+q(1+ak+nak-a-k-nk)
上記においてナッシュ均衡が成立する際には、kやqの値を変化させてもEVが変化しない。つまり、
①の式におけるkの係数が0になるものがナッシュ均衡におけるqの数値
②の式におけるqの係数が0になるものがナッシュ均衡におけるkの数値
ということになります。
ややこしいこと言ってるように見えるかもしれませんが
要はQのbet頻度やKのcall頻度によって
polar側のEVの値が変化しないケースを考えましょうって話。
ってことで実際に計算してみるとこんな感じになります。
(noteの文字だと表記上見にくいので画像で載せます)

いざ答えを見てみると意外とシンプルで
①bet sizeとレンジ内のA/Q比率でQのbet頻度は決まる
②bet sizeだけでK側のcall頻度は決まる
③bet sizeだけで最適なvalue:bluff比率も決まる
ってな話ですね。
(特にこの場合のKのcall頻度をMDFと言います)
またこの場合のpolar側のEVを計算するとそれぞれ下記のようになります。
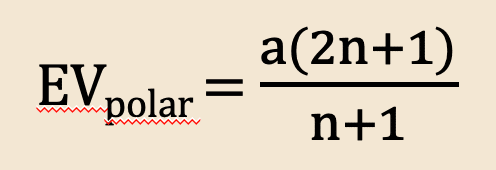
condensed側のEVは1から上記を差し引いたものになります。
ただ、condensed側はレンジEVよりもcall ActionのEVの方が重要で
それについて解説すると長くなりすぎるのでまた別の機会に。
(俗に言う"indifferent"ってやつです)
大事なのは上記のEVの式です。
このEVの式の重要なのは
nの単調増加関数であるということ
です。nを大きくすればするほどEVの値は大きくなる、つまり
bet sizeを大きくすればするほどEVは大きくなる
ってことなんです。
(厳密にはaの値でnの値は範囲指定されるケースもありますが、ややこしいのでここでは省略します)
数学の授業は一旦ここまでにして、実際に計算したものを見てみましょう。
A : Q = 50% : 50%とした上でbet sizeを10%〜300%まで変化させた場合のナッシュ均衡におけるpolar側のEVの変化です。
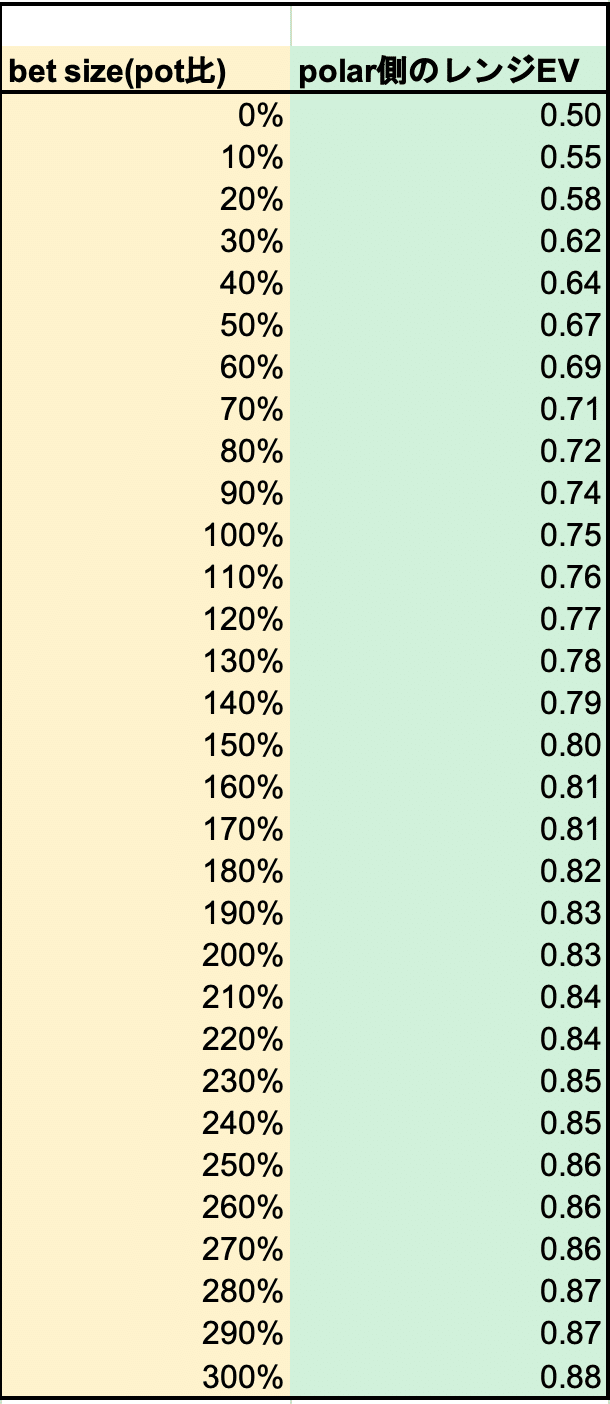
徐々にEVの上がり幅は小さくなりますが、それでもbet sizeを大きくすればするほどEVは大きくなります。
つまり、bet sizeが規定されていないAKQゲームにおいては
polar側のEVを最大化するbet sizeはAIだってことです。
そういえばみさわさんがいつも
"ポーカーはAIを目指すゲームだ"
っておっしゃってましたが、
それは何も強いハンドでMax valueとりましょうみたいな話ではなく
bet sizeを大きくすればするほどpolar側のEVがデカくなるからってことだったんですね。
(本当にその意図だったかは分かりません。笑)
もちろん実践においてはAKQゲームほど状況は単純ではないので
何でもかんでも強いハンドをAIしましょうって話にはなりません。
ただGTO Wizardのsolutionを見ていると
少なくともNuts級を持っていればIPからAIの頻度は基本存在します。
(よっぽどRiverでのSPRが大きい場合は別)
それはAIをするという選択肢が最もレンジEVを高める方法だからですね。
(適切なvalue/bluff比を保っていればの話)
ヨコサワポーカーチャンネルでもこれに近いことを言ってましたね。
▼▼▼
この辺の話です。

「相手を降ろす」という表現が最適かはさておき、
bet sizeが大きくなる
→より多くのブラフを組み込める
→自分のレンジ全体のbet頻度が上がる
ってことです。
そしてこの「自分のレンジ全体のbet頻度が上がる」ってのが実はミソで
condensed側はそもそもcall ActionのEVが0なので
(詳細はindifferentの時に書きます)
bet頻度が上がる分condensed側はレンジEVが小さくなります。
そのため、polar側はよりbet頻度を高めることで
レンジEVを最大化できるわけです。
そのためには逆に言えば
自分のレンジ全体のbet頻度を上げたい
→多くのブラフを組み込む必要がある
→bet sizeが大きくなる
でもあるわけです。
(同値なのでどっちから考えても結果は同じですが。笑)
長くなってしまったのでここまでの内容を一通りまとめましょう。
✔️ナッシュ均衡下ではお互い戦略を変えてもEVは増加しない
✔️ナッシュ均衡下では自分の戦略を変えた際に、相手が適切に戦略を変えると自分のEVが減少する
✔️bet sizeを大きくすることによって(適切にA/Q比率を守れば)レンジEVを大きくすることができる
って感じでした!
AKQゲームは他にも変数を設定する余地はあるのですが、
一旦AKQゲームはここまでにします!
次回は今回ふわっと扱ってたEVについて解説していければと思います!
ポーカーで重要になるEVとEQの関係、
そしてGTO Wizardを見てると出てくる謎のEQRについても解説していきますね!
今回は少し実践的なポーカーの話とはかけ離れてしまいましたが
次回はもう少しポーカーの実践に落とし込んだような話をしていくので
ぜひ楽しみにしておいてくださいね!✨
それでは!
(おわり)
