【熱力学2】自由エネルギー【熱力学におけるポテンシャル】
温度と外部変数だけではわからないこと
温度$${T}$$と外部変数$${X}$$で状態を指定したとします.これを次のように書きましょう.
$$
(T,X)\\
T: \text{温度,}X:\text{外部変数の組}
$$
これで私たちが手にしたのは,ただの「白地図」のようなものです.「地形」の情報は何もわかりません.どういうことか例をふたつ挙げましょう.
ある温度一定の環境のもとに一種類の気体を用意し,密度の高い系と,密度の低い系を用意したとしましょう.それらをくっつけて,仕切りに穴をあけると,図1のように,密度の均一な状態に「混ざって」ゆきます.新しい平衡状態に達した後に穴をふさいだとしても,もう何も変化しないし,再び穴をあけても何も変化しません.
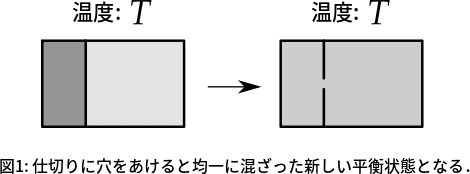
図1が,コーヒーとミルクの場合であっても同様です.これらをくっつけて,仕切りに穴をあけると,「混ざって」コーヒー牛乳ができます.この場合も,混ざって新しい平衡状態に達した後に穴をふさいでも,もうなにも変化しないし,再び穴をあけても何も変化しません.
このように,「混ざった状態」はひとりでにでき,元に戻りません(つまり,これは緩和現象の例です).山の頂上から物が転がり落ちるのは勝手に起こることと似ています.熱力学において,この山の地形を白地図上にどう表現するかが課題です.
ここで用語を入れましょう.物理では「白地図」のことを状態空間と呼び,「地形」のことをポテンシャルといいます.(ポテンシャルの正確な定義については別記事で書きました.)
熱力学において,ポテンシャルとして定義できるものが存在するとは限りませんが,下で見るように,うまく定義すると熱力学ポテンシャルというべき量が定義できます.
熱力学ポテンシャルとしての自由エネルギーの定義
「混ざった状態」は簡単には元に戻せません.しかし,コストをかければもとの状態に戻すことができます.そのコストを力学的な量である仕事(力学的な量なのできちんと測定できる!)と結びつけて理解することができれば,ポテンシャルの差を定量化することができそうです.(注: 仕事とは,系に加えた力と力を加えた方向へ動いた距離との積(正確には力の線積分)で定義される量です.)
密度が均一に混ざった気体を元に戻すには,図2のように,仕切りを適当な位置に挿入してから,その仕切りを動かせばよい.
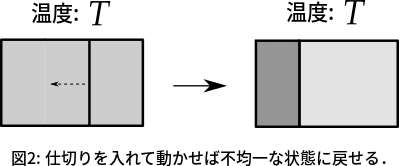
コーヒー牛乳を元に戻すには,図3のように,うまいこと濾過できる仕切りを入れて,それを動かせばよい.
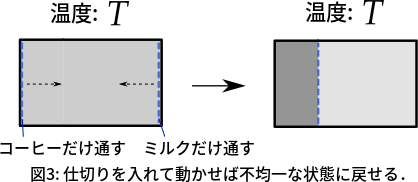
しかし残念なことに,このときに必要な仕事は,操作のやり方によって異なってきます.ゆっくりと仕切りを動かしたときと,素早く仕切りを動かしたときでは,素早く動かしたときのほうが,激しい流れが生じて無駄が大きくなり,必要な仕事が大きくなります.このように,操作の方法で異なる量をポテンシャルにするわけにはいきません.
そこで,最小の仕事で元に戻すことを考えましょう.最小の仕事であれば,一つに値が定まるため,ポテンシャルとして採用することができます.こうして定義されたポテンシャルを,ヘルムホルツ(Helmholtz)の自由エネルギーと呼びます.このノートでは,単に自由エネルギーと呼ぶことにします.この自由エネルギーは熱力学ポテンシャルのひとつで,驚くべきことに,ここに平衡状態のすべての情報が書き込まれています.そのことは今後見ていきましょう.
自由エネルギーが定義できることを次のように要請とします.
要請2: (自由エネルギーの存在)
基準となる状態$${(T,X')}$$から状態$${(T,X)}$$へ移る操作に必要な仕事に最小値が存在し,それを$${W_{\mathrm{min}}}$$と置く.このとき,
$${F(T,X)=W_{\mathrm{min}}}$$
で定義される関数$${F(T,X)}$$を自由エネルギーという.
基準となる状態とは,上の例では混ざった後の状態で,そのときの自由エネルギーの値は$${0}$$です.基準となる状態のとり方によって,自由エネルギーの値は異なりますが,値の差だけを問題にすれば,困ることはありません.
自由エネルギーの性質
次に,自由エネルギーはどんな性質を持っているか調べましょう.
系の体積が増えれば,必要な仕事も比例して増えるということがいえます.したがって,自由エネルギーは示量変数であると考えられます.
また,図1の例から,自由エネルギーが低くなる方向に状態は変化すると考えられます.そして,いつか安定な状態に達するので,新しい平衡状態は自由エネルギーが極小値となっていることが必要です.
以上から,次のことを要請として自由エネルギーに課すことにします.
要請3: (自由エネルギーの性質)
1.[示量性] 自由エネルギーは示量変数である.
2.[自由エネルギー極小の原理]新しい平衡状態は,自由エネルギー極小の状態である.(ただし,温度は変化前と後で変わらないとする.)
温度変化に関してどのように自由エネルギーが変化するかはまだ今のところわかりませんので,それはまた別の方法で探る必要があります.ひとまずそれは置いておき,この要請からどんな世界が広がっていくかを,次回は見てゆくことにしましょう.
今回のまとめ
・温度が一定の環境の下で,系の外部変数を操作したとき,必要となる仕事には最小値があると仮定し,最小の仕事を自由エネルギーと呼ぶ.
・自由エネルギーは示量性であるとする.また,自由エネルギー極小の原理によって,平衡状態は決まっているとする.
________________
更新履歴
Jan. 29, 2020 私の理論体系では自由エネルギーが定義できることは要請扱いするのが適切であると考え修正しました.
Jan. 25, 2020 執筆
クオリティの高いノートをたくさん書けるように頑張ります!
