
今週のフラクタル42 (c(x^2+y^2+3)/(z^3-1)+1)
どうも、108Hassiumです。
今回は$${\frac{c(x^2+y^2+3)}{z^3-1}+1}$$($${x}$$と$${y}$$は$${z}$$の実部と虚部)に関するフラクタル図形をお届けします。
c(x^2+y^2+3)/(z^3-1)+1
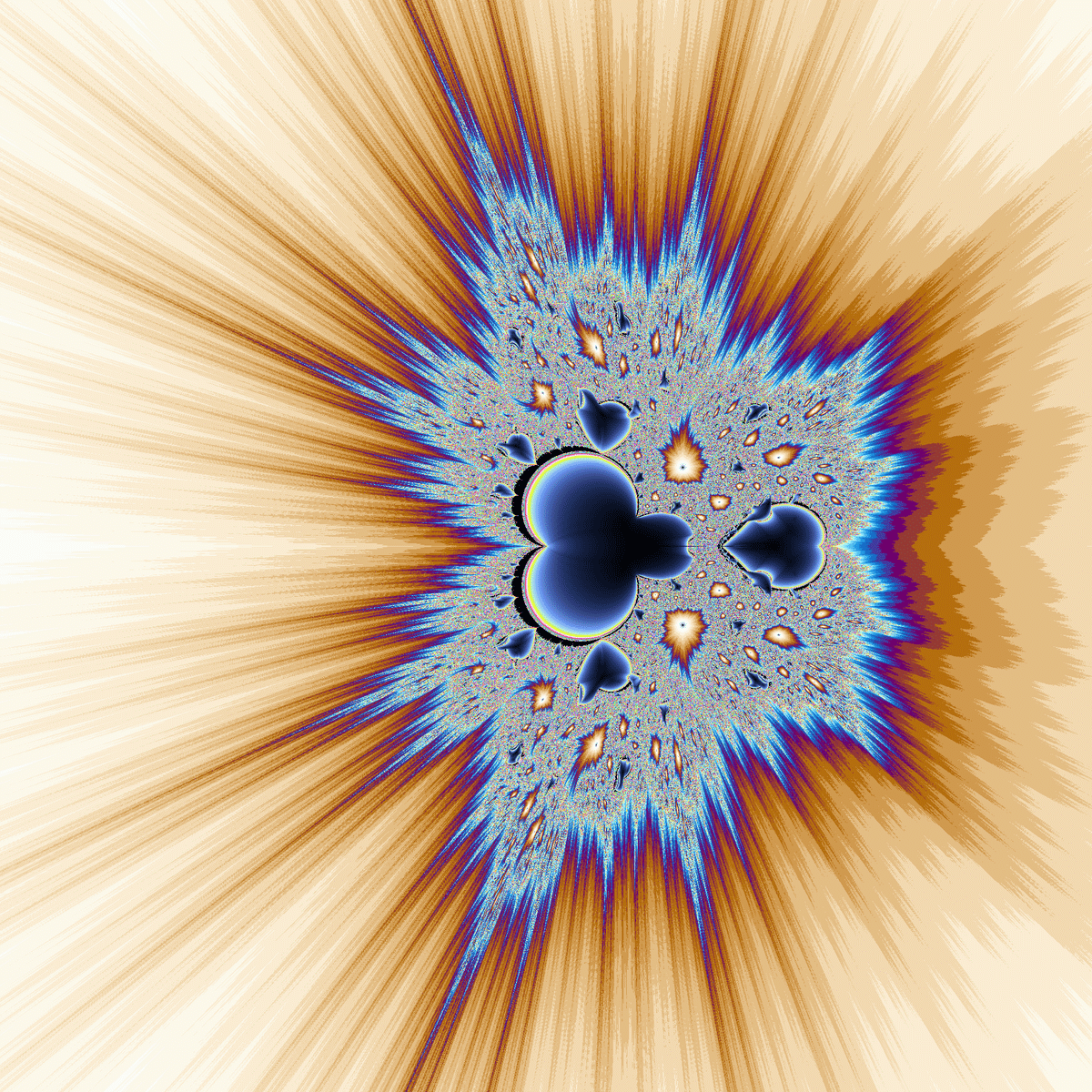
$${\frac{c(x^2+y^2+3)}{z^3-1}+1}$$は解析関数ではありませんが、1→∞→1…というサイクルを持つため解析関数でいうところの2周期発散関数と同じような性質を持つようです。
発散領域のコントラストの強さも特徴的ですが、これは$${f(z)=\frac{c(z^2+3)}{z^3-1}+1}$$としたときの$${f(f(z))}$$が$${\frac{4}{3}z}$$に漸近することと関係がありそうです。




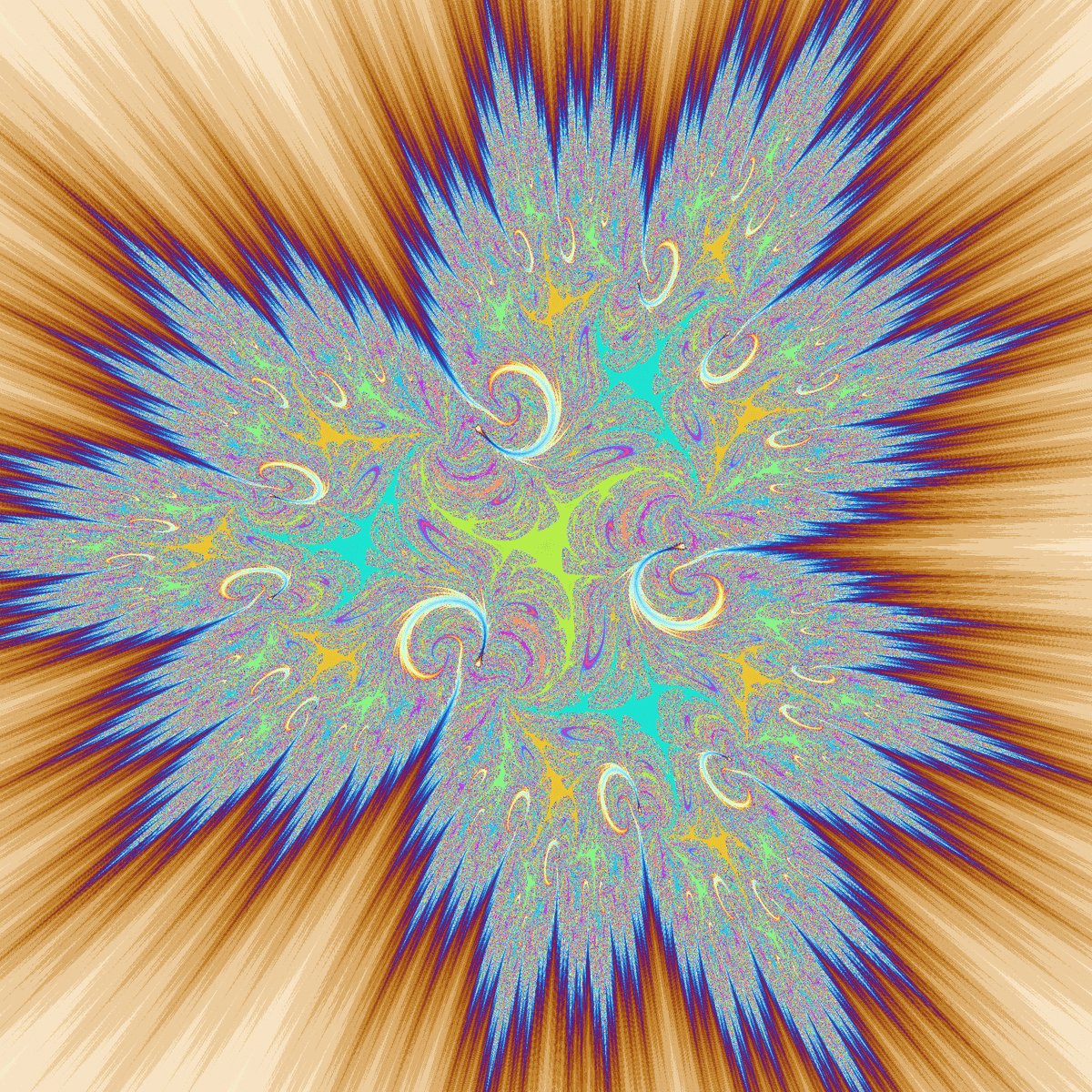



ジュリア集合は3回回転対称である点が特徴的です。


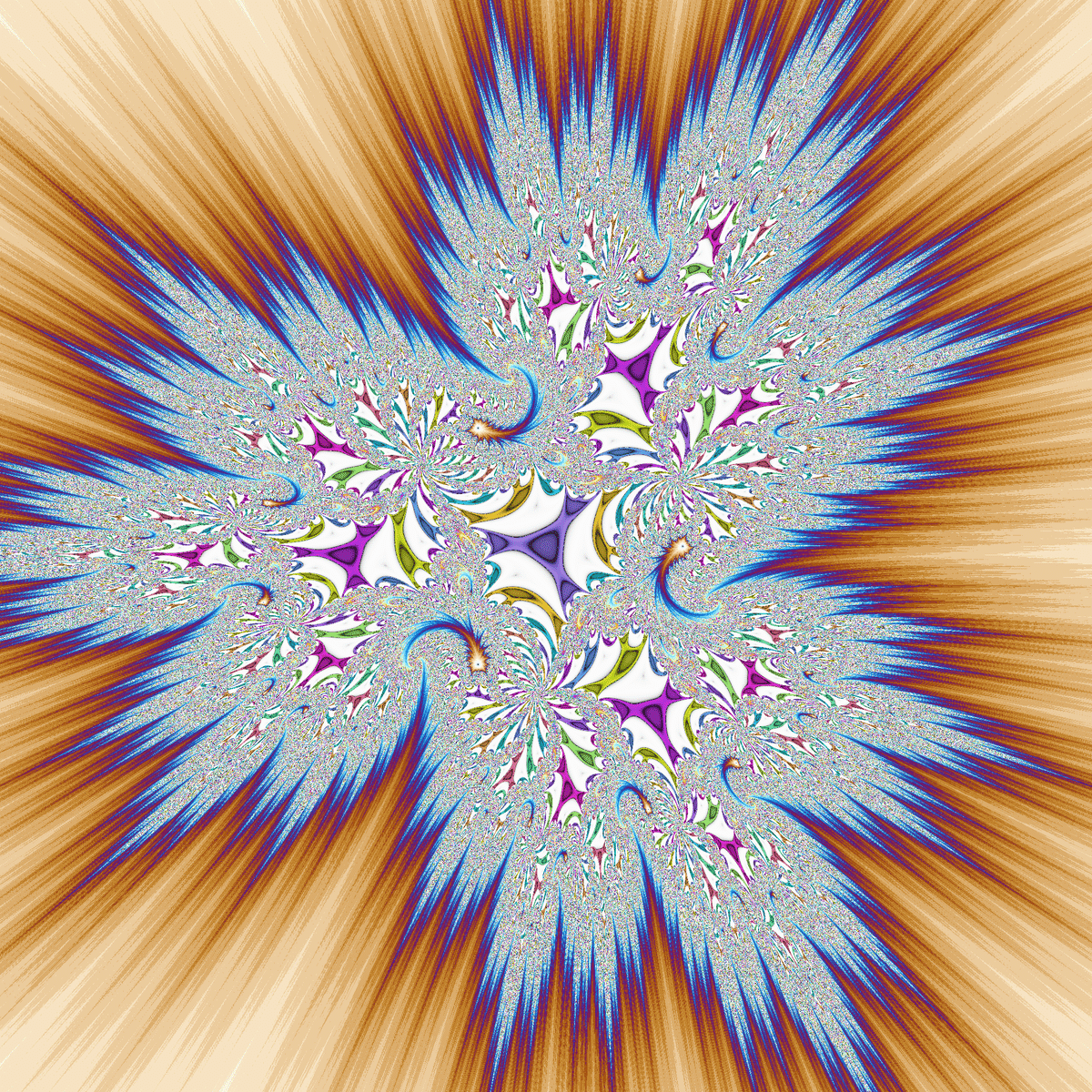


白領域のあるジュリア集合です。






いつものです。



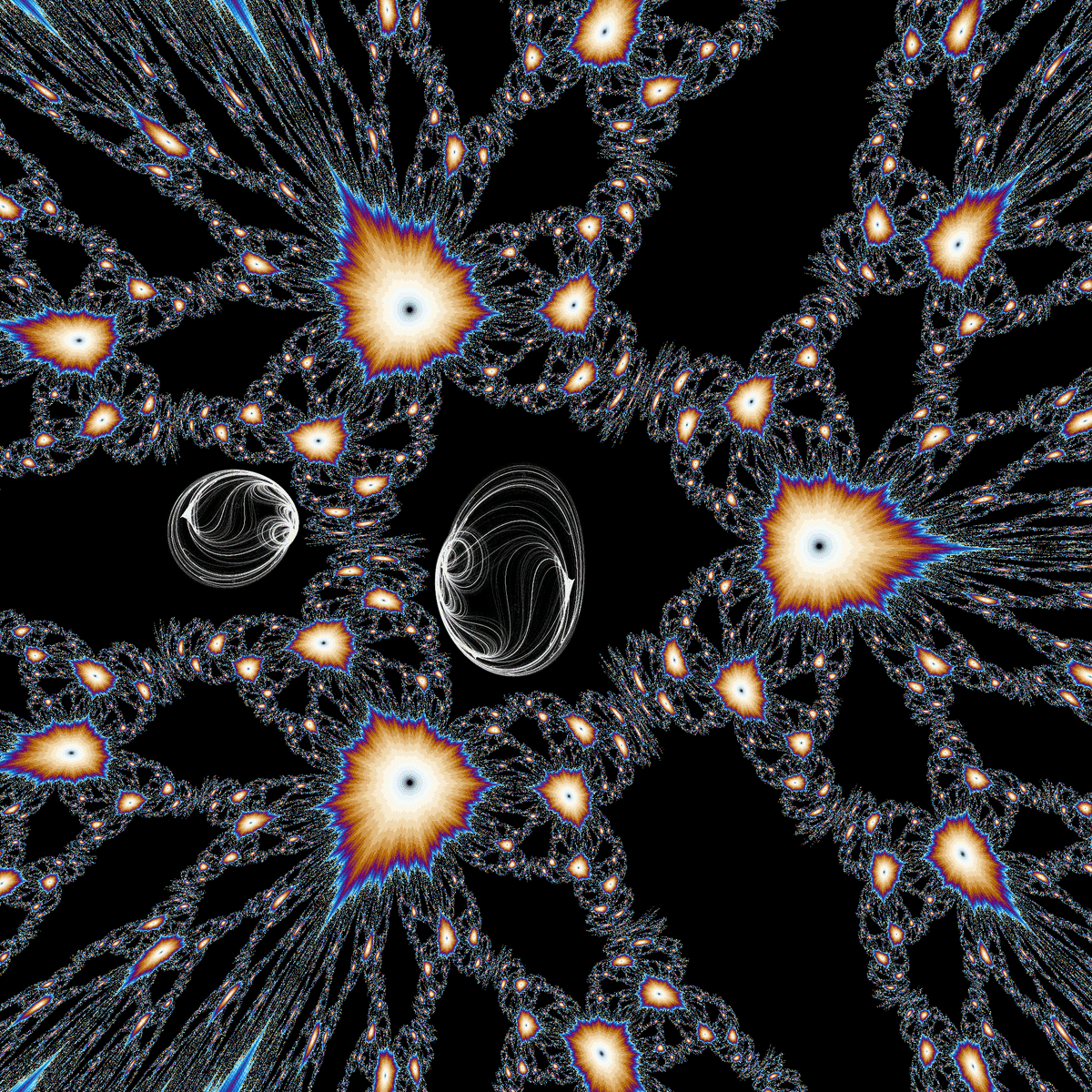

無限周期のジュリア集合とストレンジアトラクターです。
