どうも、108Hassiumです。
今週は$${(y-x+a,xy+b)}$$に関するフラクタル図形をお届けします。
(y-x+a,xy+b)
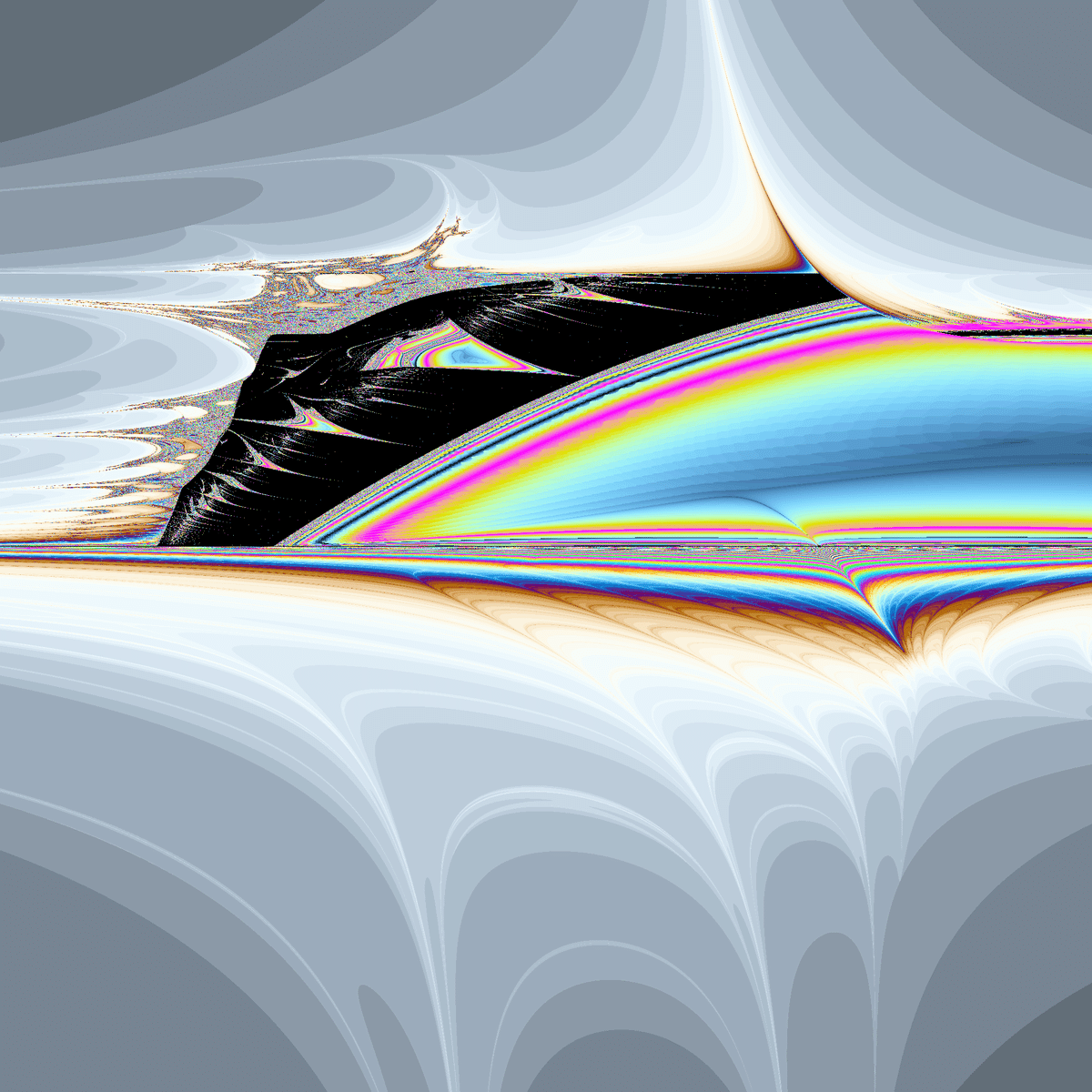☝(y-x+a,xy+b)のマンデルブロ集合(a=-3~1,b=-2~2,(x_0,y_0)=(0,0))
☝(y-x+a,xy+b)のマンデルブロ集合(a=1~5,b=-2~2,(x_0,y_0)=(0,0))以前紹介した$${(x+y+a,xy+b)}$$と式の形は似ていますが、関数としては全然別物らしくマンデルブロ集合の形は大きく異なります。
ちなみに$${(x-y+a,xy+b)}$$だと、$${(x+y+a,xy+b)}$$を上下反転させただけのマンデルブロ集合になります。
※☟$${(x+y+a,xy+b)}$$の記事
☝(y-x-0.1,xy-1)のジュリア集合
☝(y-x-1,xy-0.93)のジュリア集合
☝(y-x-1.24,xy-0.76)のジュリア集合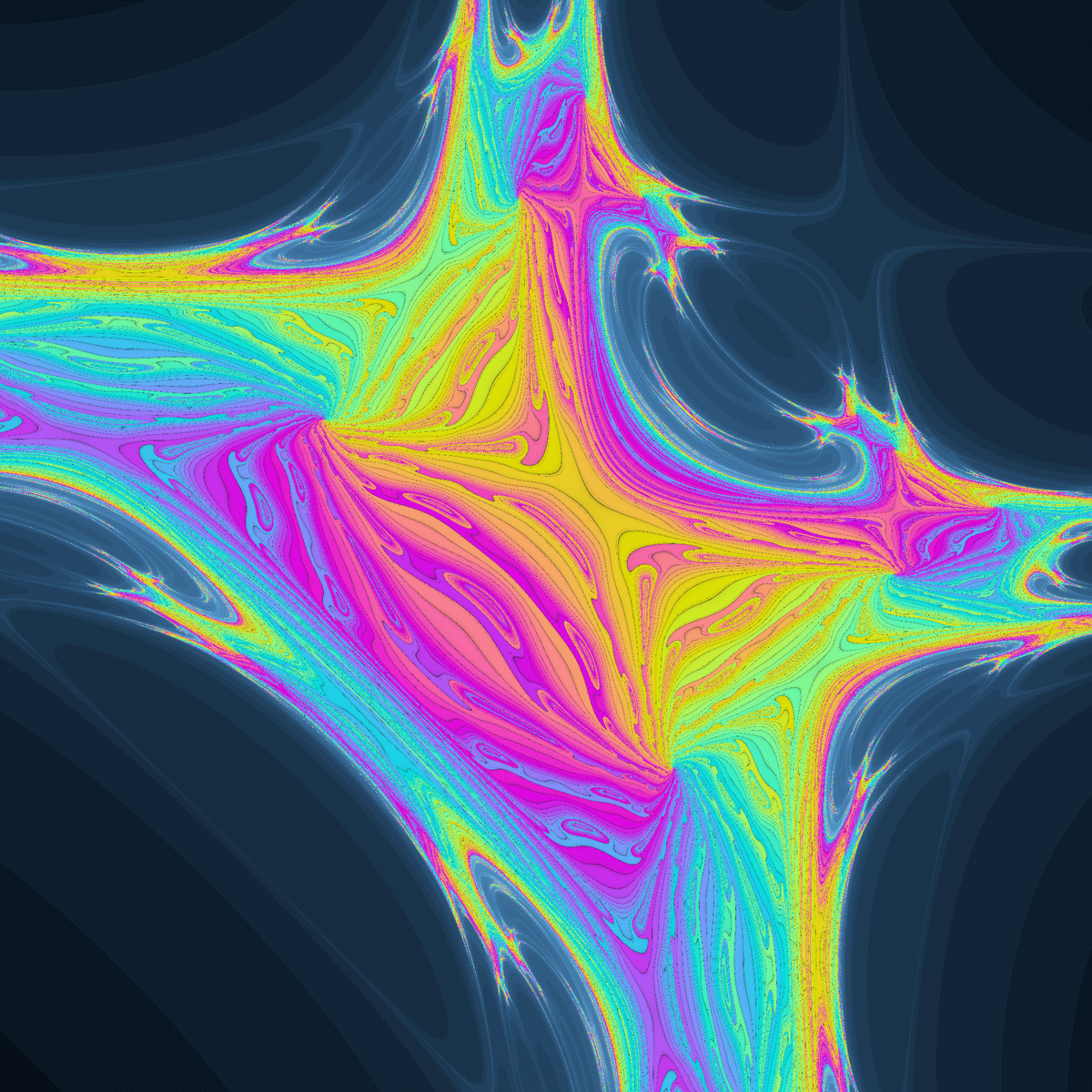
☝(y-x-1.16,xy-0.84)のジュリア集合
☝(y-x-1.97xy-0.35)のジュリア集合
☝(y-x-1.27,xy-0.78)のジュリア集合
☝(y-x-1.29,xy-0.8)のジュリア集合
☝(y-x-2,xy-0.34)のジュリア集合
☝(y-x-1.68,xy-0.56)のジュリア集合領域の境界が滑らかな曲線になっていたりする等の非解析関数によくある特徴がみられます。
☝(y-x-0.8,xy-0.96)のジュリア集合
☝(y-x-2.3,xy-0.15)のジュリア集合
☝(y-x-2.2,xy-0.2)のジュリア集合
☝(y-x+0.71,xy-0.79)のジュリア集合
☝(y-x-2.07,xy-0.29)のジュリア集合白領域($${(x_0,y_0)=(0,0)}$$の収束先ではない吸引的サイクルに収束する領域)があるジュリア集合です。
☝(y-x-1.56,xy-0.76)のジュリア集合
☝(y-x-0.66,xy-0.79)のジュリア集合
☝(y-x-1.78,xy-0.51)のジュリア集合数は少ない(しかも見た目は面白くない)ですが、吸引的サイクルが3つあるようなパラメータも見つかりました。
☝(y-x-0.84,xy-0.98)のジュリア集合(800周期)
☝(y-x-2.05,xy-0.35)のジュリア集合(1008周期)
☝(y-x-1.99,xy-0.35)のジュリア集合(1325周期)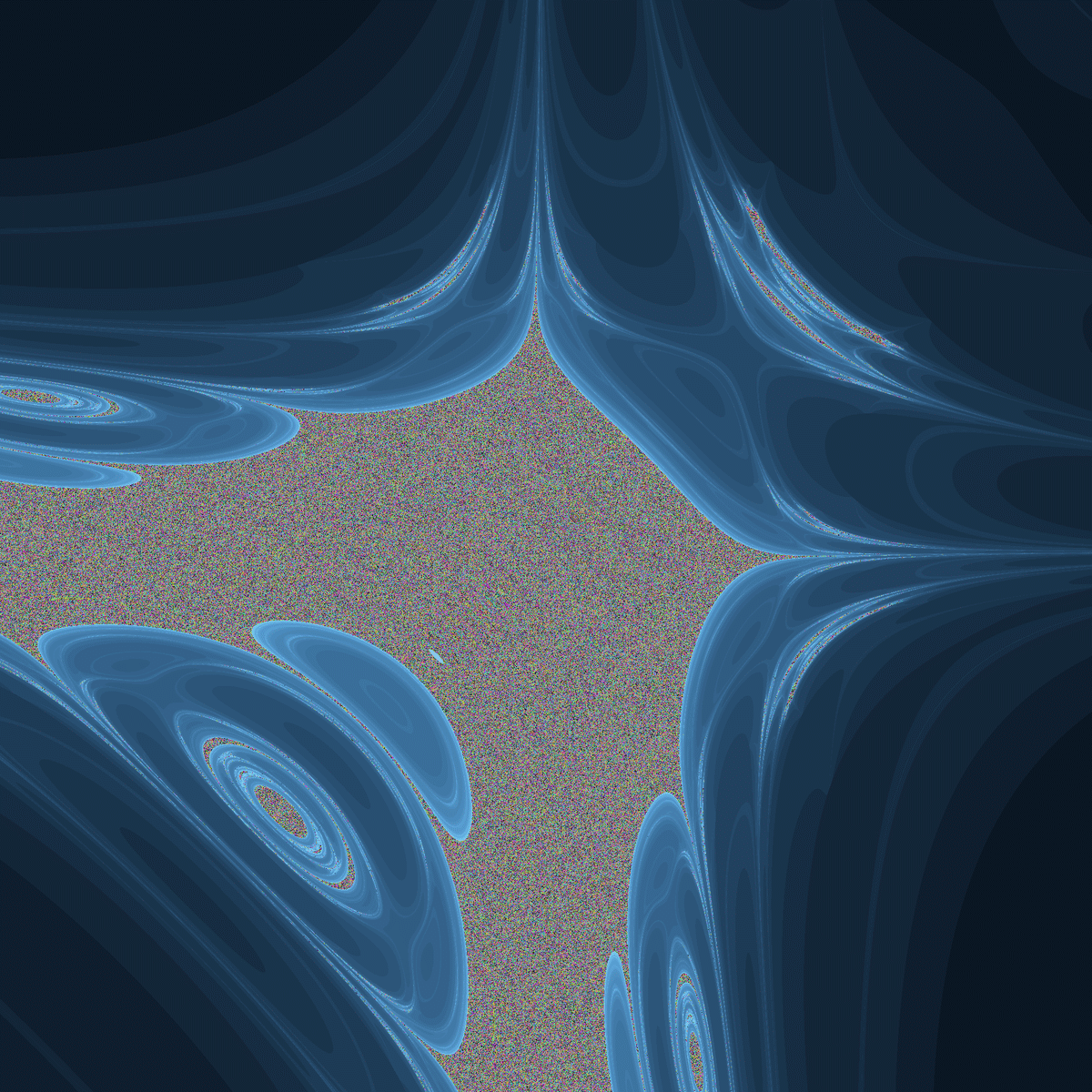
☝(y-x-2.31,xy-0.07)のジュリア集合(2094周期)
☝(y-x-0.85,xy-0.94)のジュリア集合(7552周期)いつものやつです。
非解析関数だと無限周期なのか有限周期なのか判別困難なケースが多くなってしまうため、結果の信頼性はいつにもまして低くなってしまいます。
☝(y-x+1,xy-0.79)のジュリア集合
☝(y-x-1.75,xy-0.5)のジュリア集合
☝(y-x-1.62,xy-0.64)のジュリア集合とストレンジアトラクター
☝(y-x-1,xy-0.96)のジュリア集合とストレンジアトラクター
☝(y-x-1.2,xy-0.9)のジュリア集合とストレンジアトラクター
☝(y-x-1,xy-0.91)のジュリア集合とストレンジアトラクター
☝(y-x-4.5,xy-0.1)のジュリア集合とストレンジアトラクター
☝(y-x-1.5,xy-0.8)のジュリア集合とストレンジアトラクター
☝(y-x-1.93,xy-0.48)のジュリア集合とストレンジアトラクター
☝(y-x-1.93,xy-0.5)のジュリア集合とストレンジアトラクター
☝(y-x-2.2,xy-0.23)のジュリア集合とストレンジアトラクター
☝(y-x-2.33,xy-0.2)のジュリア集合とストレンジアトラクター無限周期のジュリア集合です。
☝(y-x-0.71,xy-0.97)のジュリア集合安定領域と不安定領域が混在するジュリア集合です。
