今週のフラクタル48　(((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1)

どうも、108Hassiumです。

今回は$${\frac{c+1}{5c+4}(\frac{1}{z}-\frac{4c}{cz-2c-1})+\frac{1}{c}+1}$$に関するフラクタル図形をお届けします。

((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のマンデルブロ集合(z_0=1/(3c)+1/3)

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のマンデルブロ集合(z_0=1/(3c)+1/3)

$${\frac{c+1}{5c+4}(\frac{1}{z}-\frac{4c}{cz-2c-1})+\frac{1}{c}+1}$$は、$${f(f(f(z)))}$$が1次になるタイプの3周期発散関数です。

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.55+0.24iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=0.22+0.45iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.41+0.37iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.3+0.55iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.01+0.68iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.26+0.58iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-1.25+0.37iのジュリア集合

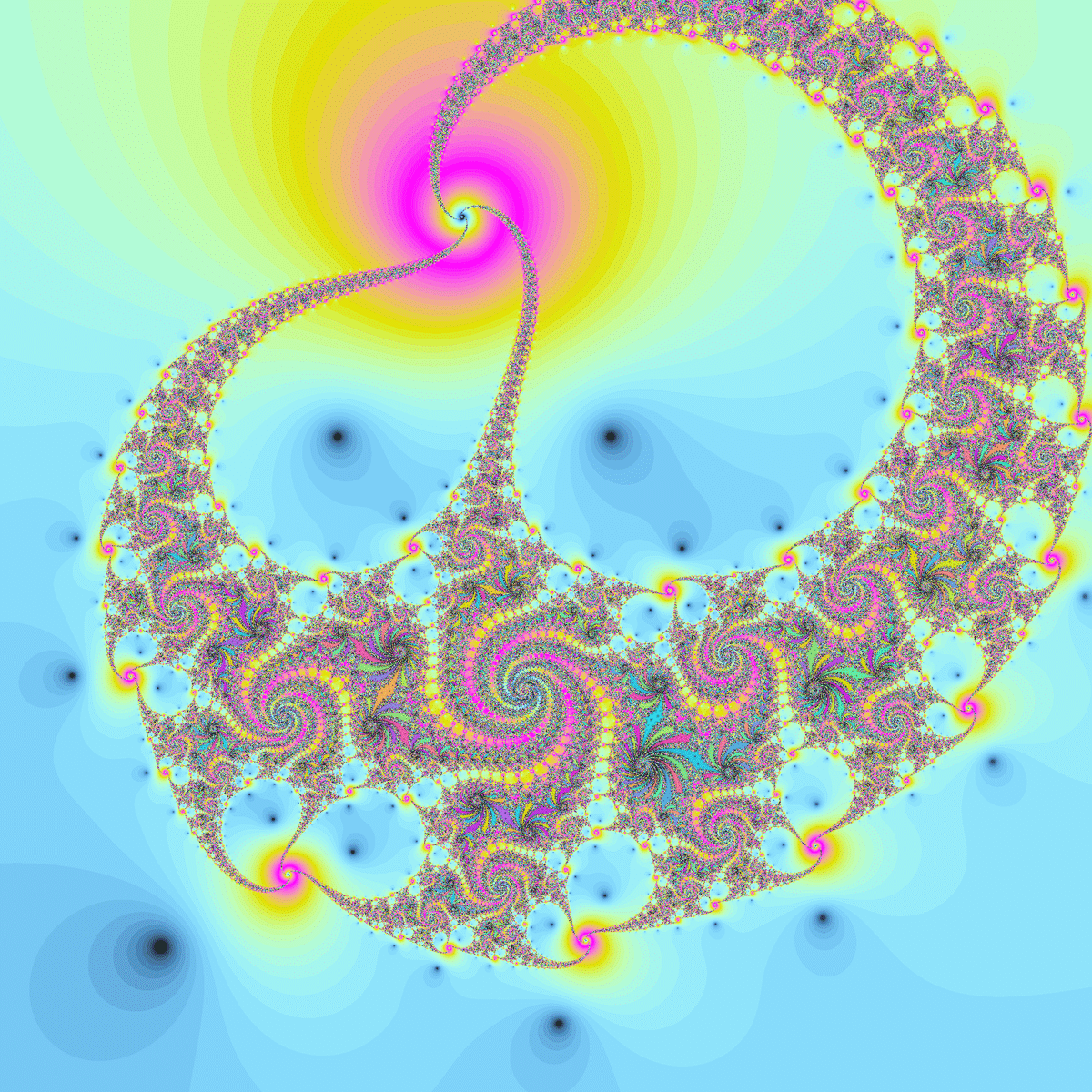
発散領域があるタイプのジュリア集合です。

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.69+0.54iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.62+0.49iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.58+0.41iのジュリア集合

発散領域が無いタイプのジュリア集合です。

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-1.02+0.54iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-0.56+0.24iのジュリア集合

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-1.12+0.37iのジュリア集合

白領域のあるジュリア集合です。

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=0.23+0.16iのジュリア集合(150周期)

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-1.27+0.33iのジュリア集合(165周期)

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-1.33+0.19iのジュリア集合(330周期)

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=-1.11+0.51iのジュリア集合(345周期)

☝((c+1)/(5c+4))(1/z-4c/(cz-2c-1))+1/c+1のc=0.24+0.4iiのジュリア集合(606周期)