
今週のフラクタル34 ((z^5+0.5iz^4)/(z+0.18i)+c 他)
どうも、108Hassiumです。
今回は$${\frac{z^5+0.5iz^4}{z+0.18i}+c}$$に関するフラクタル図形をお届けします。
(z^5+0.5iz^4)/(z+0.18i)+c
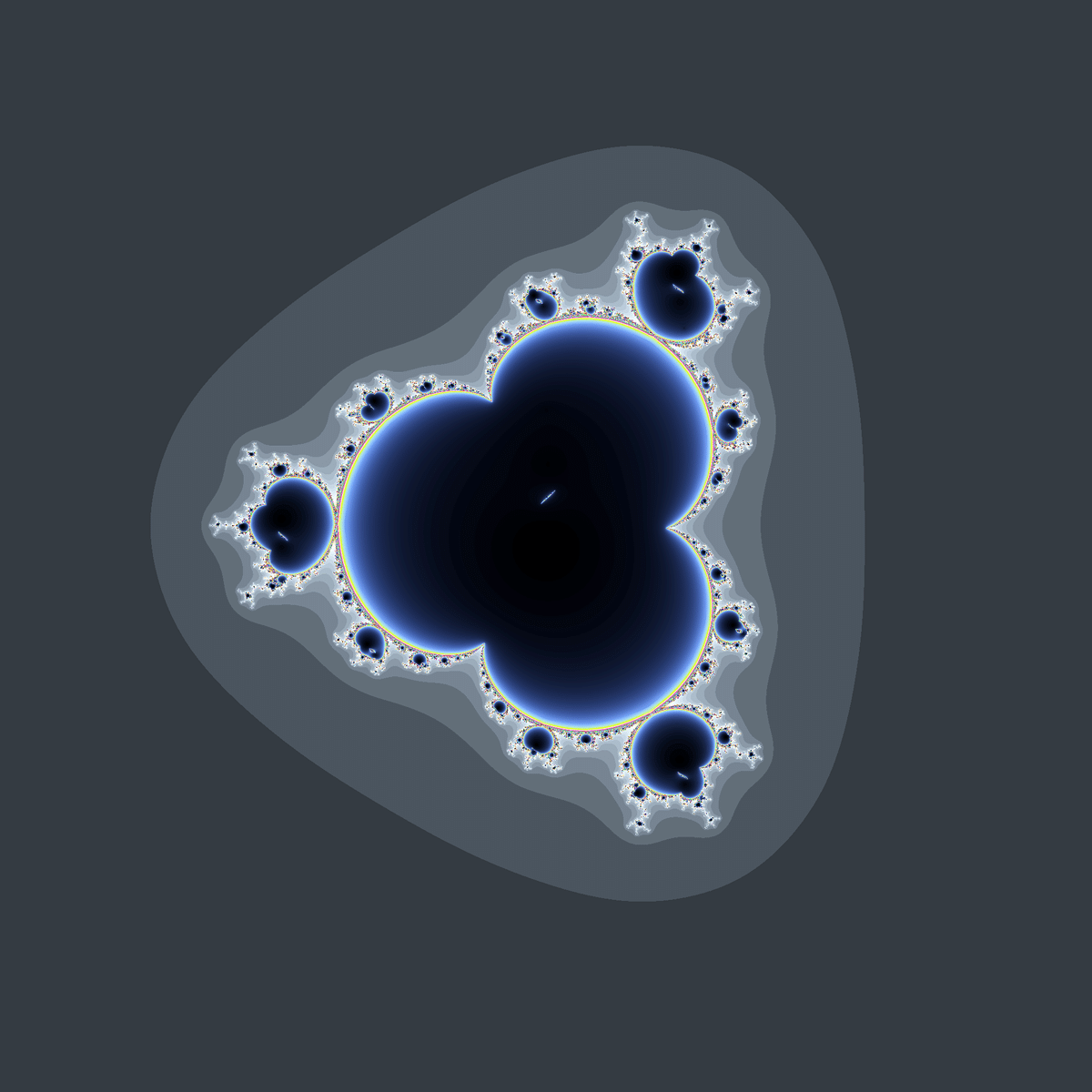

$${\frac{z^5+0.5iz^4}{z+0.18i}+c}$$は$${z^4+c}$$に摂動を加えた関数なので、マンデルブロ集合の概形は$${z^4+c}$$に似ていつつも細部が崩れたような見た目になっています。
臨界点は$${z=0}$$と$${z=-0.3i}$$の2点で、多重度は$${z=0}$$が3重、もう片方は2重です。





拡大図です。




ジュリア集合は崩れたり欠けたり変な領域があったりとバラエティ豊かな特徴を持っていますが、全体の大まかなシルエットは$${z^4+c}$$のものと似ています。



$${z^3+c}$$のジュリア集合で見られるような三角形の収束領域と、$${z^4+c}$$のもののような四角い領域が混在するジュリア集合です。






いかにも摂動系の関数っぽい奇抜な見た目のジュリア集合です。




白領域のあるジュリア集合です。
今まで紹介してきた摂動系の関数でよく見られたような構造の白領域は、この関数ではほとんど見られませんでした。
※☟摂動系の関数でよく見られる白領域の構造の例

おそらく白領域に対応する臨界点の多重度が2(過去に紹介したものは全て1)であることと関係があると思うのですが、詳細は不明です。





いつものです。
(z^5+0.75iz^4)/(z+0.27i)+c


$${\frac{z^5+0.75iz^4}{z+0.27i}+c}$$は、$${\frac{z^5+0.5iz^4}{z+0.18i}+c}$$の摂動の影響を強めたものです。


臨界点の多重度の組み合わせも$${\frac{z^5+0.5iz^4}{z+0.18i}+c}$$と同じ(3重と2重)はずなのですが、なぜかより多重度の大きい関数のような特徴を持つジュリア集合が見られました。
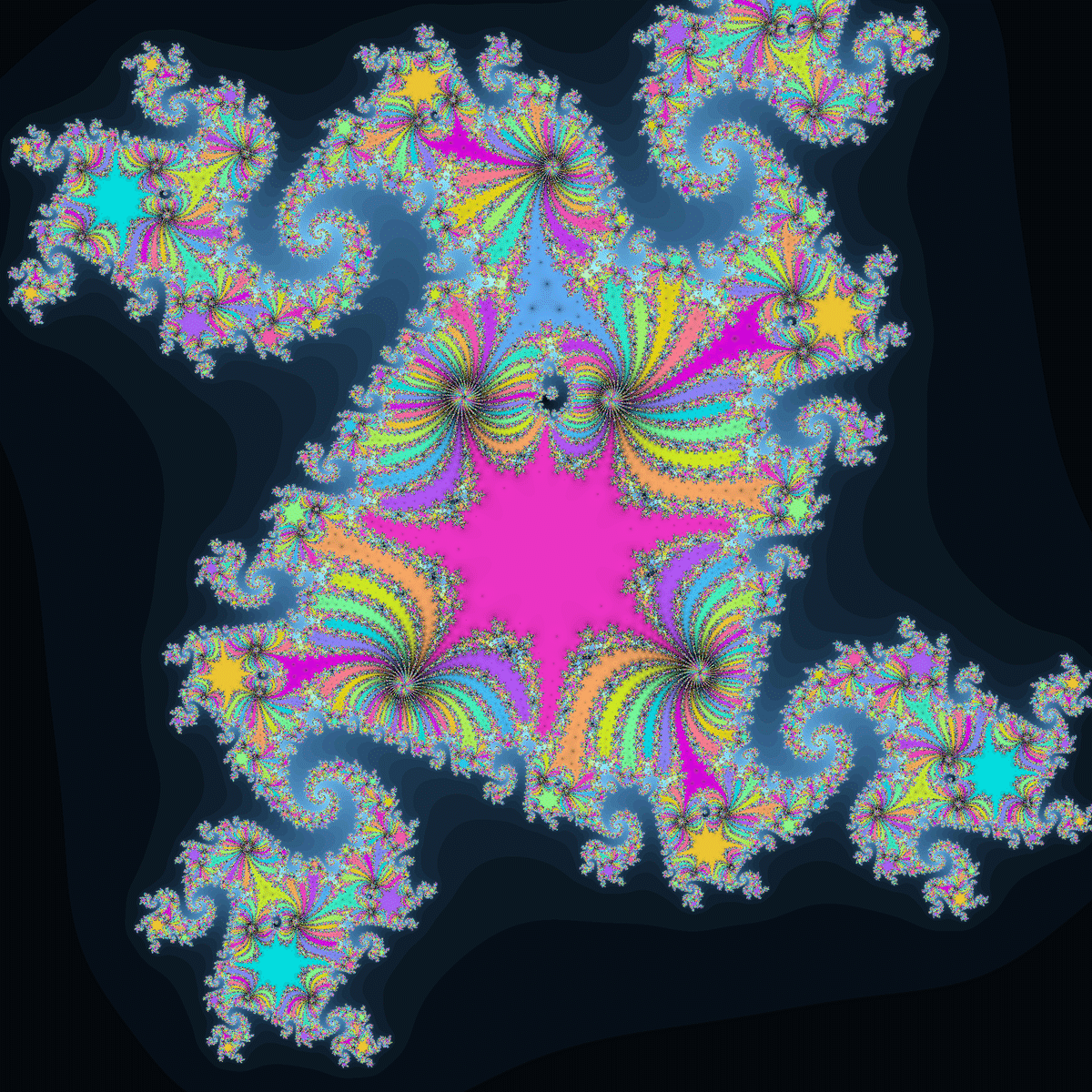



先述の通り$${\frac{z^5+0.75iz^4}{z+0.27i}+c}$$は$${\frac{z^5+0.5iz^4}{z+0.18i}+c}$$の摂動を強めた関数なので、形の崩れ方も激しいような気がします。





アレです。
(z^n+bz^(n-1))/(z+a)^m+c
$${f(z)=\frac{z^n+bz^{n-1}}{(z+a)^m}+c}$$という関数は、以下のような性質を持ちます。
$${a\rightarrow0}$$で$${z^{n-m}+bz^{n-m-1}+c}$$に収束。
臨界点は3つで、そのうち1つは$${z=0}$$。
臨界点の多重度は$${z=0}$$が$${n-2}$$、他の2点が1。
$${a=b=0}$$だと$${f(z)=z^{n-m}+c}$$なので、$${a}$$と$${b}$$が両方とも小さければ以前紹介した$${\frac{z^n}{(z+a)^m}+c}$$と同様に「$${z^{n-m}+c}$$に摂動を加えた関数」と見做すことができます。
3つある臨界点のうち、$${z=0}$$以外の2つは2次方程式を解くことで求められます。
そして$${a}$$と$${b}$$の値を微調整することで、2つの臨界点を重ねて1個の2重臨界点にすることができます。
まず、$${f(z)}$$を微分してみます。
$${f'(z)\\=\frac{(nz^{n-1}+(n-1)bz^{n-2})(z+a)^m-m(z+1)^{m-1}(z^n+bz^{n-1})}{(z+a)^{2m}}\\=\frac{(nz^{n-1}+(n-1)bz^{n-2})(z+a)-m(z^n+bz^{n-1})}{(z+a)^{m+1}}\\=\frac{nz^n+(n-1)bz^{n-1}+naz^{n-1}+(n-1)abz^{n-2}-mz^n-mbz^{n-1}}{(z+a)^{m+1}}\\=\frac{z^{n-2}((n-m)z^2+(na+(n-m-1)b)z+(n-1)ab)}{(z+a)^{m+1}}}$$
$${(n-m)z^2+(na+(n-m-1)b)z+(n-1)ab)=0}$$が2重解を持てば$${f(z)}$$の$${z\neq0}$$の臨界点が2重臨界点になるので、2次方程式の判別式を計算します。
$${(na+(n-m-1)b)^2-4(n-m)(n-1)ab\\=n^2a^2+2n(n-m-1)ab+(n-m-1)^2b^2-(4n^2-4n-4mn+4m)ab\\=n^2a^2+(-2n^2+2mn+2n-4m)ab+(n-m-1)^2b^2}$$
これが0になれば2重解になるのですが、有理数解が欲しいので$${a}$$についての2次方程式として判別式を計算します。
$${(-2n^2+2mn+2n-4m)^2b^2-4n^2(n-m-1)^2b^2\\=4b^2((n^2-mn-n+2m)^2-(n^2-mn-n)^2)\\=4b^2(n^2-mn-n+2m+n^2-mn-n)(n^2-mn-n+2m-(n^2-mn-n))\\=16b^2m(n^2-mn-n+m)}$$
$${16b^2m(n^2-mn-n+m)}$$が有理数の2乗になれば$${n^2a^2+(-2n^2+2mn+2n-4m)ab+(n-m-1)^2b^2=0}$$は有理数解を持つのですが、$${16b^2}$$は有理数の2乗であることがわかり切っているので結局は$${m(n^2-mn-n+m)}$$が平方数になればいいことがわかります。
以上の計算をまとめると、
$${f(z)}$$の$${z\neq0}$$の臨界点が2重臨界点になるには、$${z}$$の2次方程式$${(n-m)z^2+(na+(n-m-1)b)z+(n-1)ab)=0}$$が2重解を持てばよい。
$${(n-m)z^2+(na+(n-m-1)b)z+(n-1)ab)=0}$$が2重解を持つには、$${a}$$と$${b}$$が$${n^2a^2+(-2n^2+2mn+2n-4m)ab+(n-m-1)^2b^2=0}$$を満たせばよい。
$${n^2a^2+(-2n^2+2mn+2n-4m)ab+(n-m-1)^2b^2=0}$$を満たす$${a}$$と$${b}$$が有理数になるためには、$${m(n^2-mn-n+m)}$$が平方数になればよい。
・・・という風になります。
これ以上の分析は私には無理そうなのですが、幸運にも(?)$${m=1}$$とすると$${m(n^2-mn-n+m)=n^2-2n+1=(n+1)^2}$$になるので、分母の次数に拘らなければ目的の関数を得ることができます。
$${1< m}$$の場合、$${m(n^2-mn-n+m)}$$が平方数になる組み合わせとしては以下のようなものがあります。
$${n-m=2:(m,n)=(8,10)}$$
$${n-m=3:(m,n)=(6,9)}$$
$${n-m=5:(m,n)=(5,10)}$$
$${n-m=6:(m,n)=(3,9)}$$
$${n-m=7:(m,n)=(8,15)}$$
$${n-m=8:(m,n)=(2,10),(7,15)}$$
※$${n-m=4,9}$$は解無し?
