『数式組版』を組む技術：ディスプレイ数式(2)

本稿において，“本書”とは木枝祐介著『数式組版』ラムダノート（2018）のことである．
>>> https://www.lambdanote.com/collections/mathtypo
また，本書はLuaLaTeXを用いて組まれた．したがって本稿ではLuaLaTeXの使用を前提としている．
本書が組まれた当時はTeX Live 2017が用いられたが，多くのコードはそれより後のTeX Live 2019まで共通して使用可能である．
本稿では，バージョンに強く依存する場合を除いて，各バージョンは明記されないことがある．

連立(1)

本稿で扱うのは，次のようなディスプレイ数式である（連立については本書を参考のこと）．

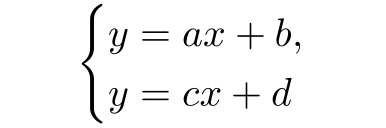
◆式の接近
とくに，次の連立にあるディスプレイ数式を例にとる．

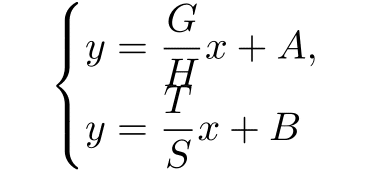
この状態で顕著な問題点である2本の式の接近状態の解消を考える．
ここで，それぞれの式の形は変更してはいけないという条件を付け加える（そしてこの条件はしばしば実務上の条件にもなる）．
すなわち，接近状態にある式を離す方策のみ考えることとする．

いま，このディスプレイ数式は，次のようなコードによって組まれている．

\everymath{\displaystyle}
...
\begin{eqnarray*}
\left\{
\begin{array}{@{}l@{}}
y = \frac{G}{H}x + A,\\
y = \frac{T}{S}x + B
\end{array}
\right.
\end{eqnarray*}

◆古典的な局所的解決
よくしられた局所的解決方法は`\\`にオプション引数を与えることである．

\everymath{\displaystyle}
...
\begin{eqnarray*}
\left\{
\begin{array}{@{}l@{}}
y = \frac{G}{H}x + A,\\[2ex]
y = \frac{T}{S}x + B
\end{array}
\right.
\end{eqnarray*}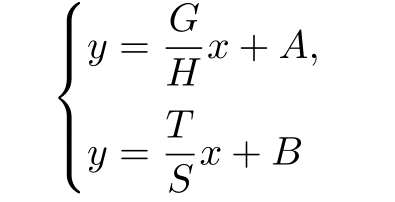

ここでは，`\\`のオプション引数にひとつの例として`2ex`の値を与えた．
この`ex`はxハイトの大きさである．
TeXの意味でより正確には，当該TFMにおける`FONTDIMEN`プロパティ中の`XHEIGHT`で定義された値（これは`\fontdimen5\font`でアクセス可能）である．
この`2ex`という値が適当か否かについては本稿ではふれないことにする．