期待値の上振れ、下振れについて考察

0. はじめに

経験豊富な方は体感や経験で理解していて、必要がない話ではありますが、今回の目的は、簡易な統計学の計算とシミュレーターによる検証を加えることで、より直感的に理解しやすくなればと思いました。

1. 結論

・マイジャグラー4の設定4を1日8000G✕20日間実施した際、だいたいの人(約68%)の収支は、＋15万～+60万の範囲に収まると言えそうです。(等価)

・マイジャグラー4の設定4を1日8000G✕20日間実施した際、ほとんどの人(約95%)の収支は、-6万～+85万の範囲に収まると言えそうです。(等価)

・1日8000G✕20日✕12ヶ月継続した場合、だいたいの人(約68%)は+400万以上であり、期待値+470万に近くなる。95%範囲の下限でも+310万以上になる。

・平均機械割が高い方が、収支振れの幅が小さく安定する。

・1日8000G✕20日間のシミュレートを100人分実施した結果の上位10名、下位10名の総収支は2SD(95%)の範囲に収まっていた。
試行を重ねれば重ねるほど、2SDの範囲を超える人が発生するが、極めて稀なケースと言えそうです。

・1日8000G✕20日間のシミュレートを100人分実施した結果の下位30人はSD(68%)の範囲を超えた。上位30人はSD(68%)の範囲に収まった。試行数が少ないため、結論づけはできないが100人中70人はSD(68%)の範囲内にいることを確認しました。

2. シミュレーション条件

※独自作成の仮想プログラムのため、実機と完全一致ではありません。

対象機種：マイジャグラー4
設定: 設定4 (機械割 約104.3%)
試行回数：8000G✕20日分 (16万G)
ループ回数：100回 (計1600万G)
期待差枚：16万Gあたりの期待差枚は約+2万枚

3. シミュレータ結果 設定4 8000G✕20日

8000G✕20回を一ヶ月として、100人分実践した場合のワースト10人とベスト10人のデータを掲載します。
約-5万円～+60万円くらいの幅に収まっています。(等価)

4. 標準偏差と95%信頼区間

試行回数と確率分母がわかれば、標準偏差の計算が可能です。

期待値と標準偏差(SD)により、全体の約68%のデータが収まる範囲がわかります。

例えば、マイジャグラー4 設定4のBIG確率は1/264.3、これを8000G実施した場合の標準偏差は5.49になります。期待BIG回数は8000 / 264.3 = 約30回

マイジャグラー4の設定4を8000G回をものすごく大量実践した場合の約68%のデータが次の範囲に収まると言えそうです。
24.51回 (30-5.49)<= BIG回数 <= 35.49 (30+5.49)

同様の考え方で、標準偏差の1.96倍=1.96SDを計算すれば、全体の約95%が収まる範囲がわかります。
1.96SD = 10.76になりますので、マイジャグラー4の設定4を8000G回を実践すれば、ほぼ次の範囲に収まると言えそうです。
19.24回 (30-10.76)<= BIG回数 <= 40.76 (30+10.76)

学校の偏差値で言えば、SDは40-60程度で良くいる範囲、1.96SDは35とか70以上とか少し希少な範囲と例えられます。

次の章からは、8000G✕20日実践した場合に想定される収支の下振れ、上振れをSD、1.96SDに注目して計算していきます。

5. 統計計算結果 設定4 8000G✕20日

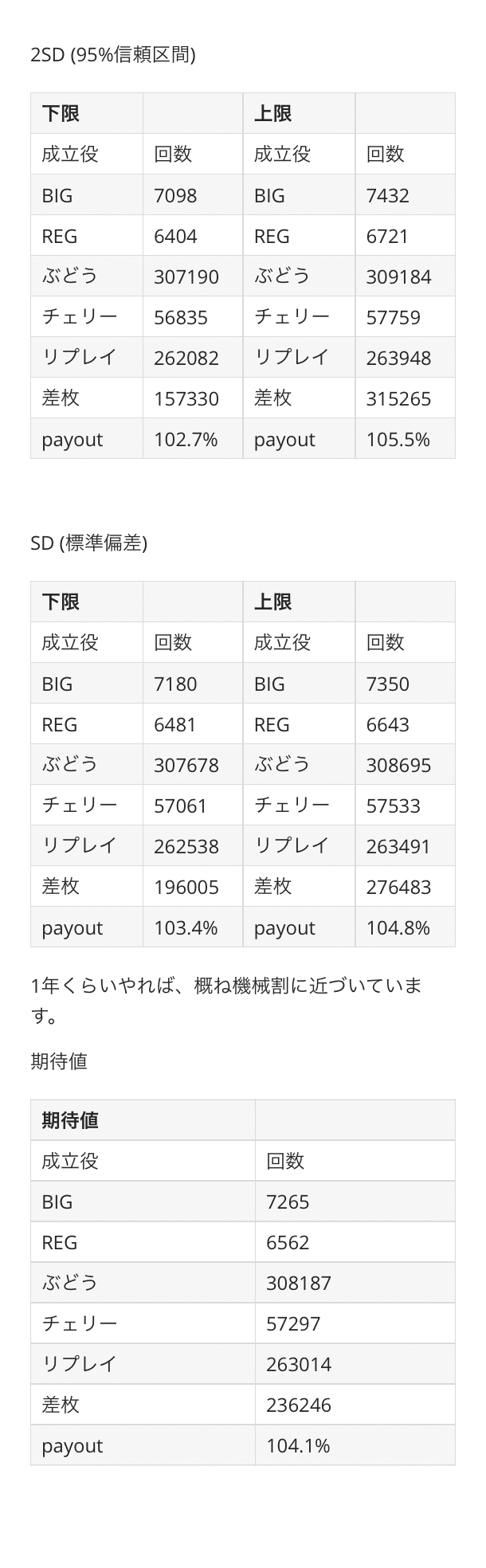
マイジャグラー4 設定4を8000G✕20日実践した場合に想定される差枚数を計算しました。
期待値、SD(68%)、2SD(95%)ごとに計算しています。

収支の偏りは、次の画像のような２項分布のグラフで表現され、山のTOPが期待値で一番発生しやすい。SDで囲まれたエリアの面積で全体の約68%、2SDの面積が全体の約95%になります。
※画像作成不備 2SD -> 1.96SD

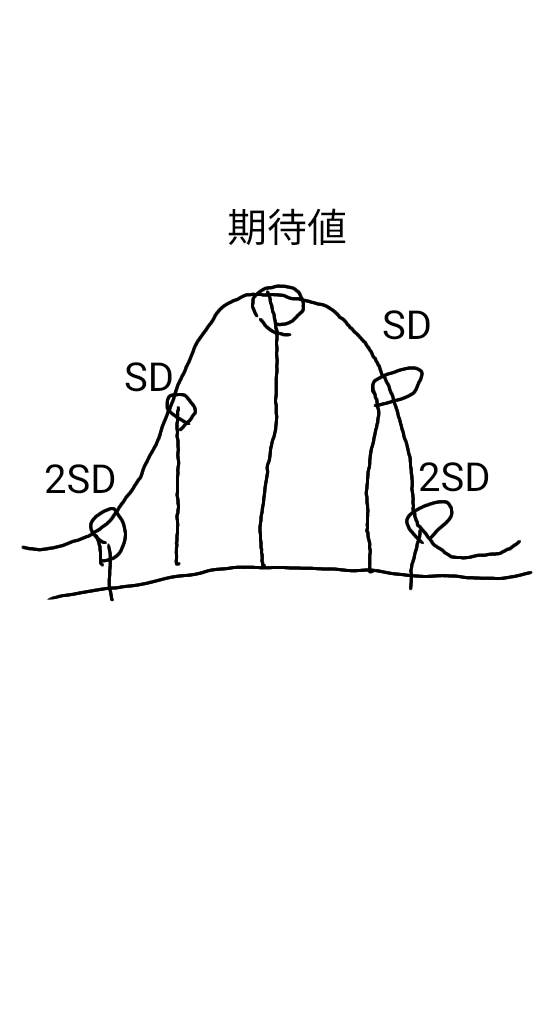
期待値104.1%に対して、8000G✕20日分実施したとき
だいたいの人はSDの範囲内である、約+15万～+60万の範囲に収まるのだろうと推測できます。

引きが強かったり、弱かったりしても、ほとんどの場合は1.96SDの範囲内である、約-6万～+85万の範囲に収まるのだろうと推測できます。

※金額は等価計算していますので、実際は換金ギャップや持ちコイン比率で大きく変わります。
(都内 46枚-52枚だと、期待収支から10%-20%程度下がると思います。)

試行回数が増えたり、平均機械割が上がる場合は、下限と上限の割合が小さくなっていきます＝収支が安定しやすくなります。

今回のようなシンプルなA-typeではなく、もう少し引きによって展開の幅が効いてくる機種の場合は、同じ機械割でも収支振れ幅が広くなると思いますが、計算は現在できていないです。

6. 統計計算結果 設定5 8000G✕20日

7. 統計計算結果 設定3 8000G✕20日

8. 統計計算結果 設定4 8000G✕20日✕12ヶ月