
新型コロナウイルスの感染者数の増減を片対数グラフで表す理由
新型コロナウイルス関連で、毎日数値がアップデートされ、様々なチャート、ダッシュボードが登場しています。ここでは、時系列の感染者数の推移を示すことで何を知りたいのか、という観点で、チャート表現を整理しました。
目次
・片対数スケール + 時系列にて、新規症例数の指数関数的変化を知りたい
・両対数スケールにて、確定症例数の指数関数的変化を知りたい
・線形スケールのエリアチャートにて、感染者とその内訳(治癒者、死者、治療中etc)の推移を知りたい
・ダッシュボードで何を伝えるべきか
片対数スケール + 時系列にて、新規症例数の指数関数的変化を知りたい
様々に引用されているわかりやすいチャートの一つ、イギリスFinancial Times掲載のチャートをみると、横軸が各国で症例百件目を超えた日からの日数、縦軸が累積の確定症例数が対数スケールとなっています。二軸あるうち片方だけ対数スケールなので片対数スケールと呼びます。縦軸はよくみると、100から始まり、200、500、1000、2000と不自然な増加を見せています。

よくみなれた数値が等間隔のスケールは線形スケール、それに対して今回使用されているものが対数スケールとなります。スケールというのはデータを如何に視覚的に表現するかの変換ルールを指し、今回は配置として視覚化しています。
線形スケールでは絶対値を示しますが、対数スケールでは、相対値を示します。
絶対値で計算するとたとえば、2-1=1、101-100=1となり、1と2の間と100と101の間が、同じ数値(距離)になります。
相対値で計算すると、1と2の間は100%の増加となりますが、100と101の間は1%の増加となります。この場合、100と101の間の距離は、1と2の間の距離の100分の1となります。

軸の目盛りはこれらを反映させたものとなります。
対数スケール上での同じ距離=同じ相対値(パーセンテージ)での増加や減少を示しています。同じ相対値での増加や減少を指数関数的増加・減少といい、経済成長、マルチ商法の広がり、ムーアの法則、ウイルスの蔓延などを説明する際によく利用されます。そして同じ距離=同じ相対値はチャート上で直線として現れます。
つまり、対数スケールを用いたチャートで直線が現れる場合、それが指数関数的に増加・減少していることを表します。今回の場合は、
・感染者数自体が、指数関数的に増加するため、実態に即している。
・過去の数値や未来におけるシナリオ別の変化量を直線で想起することができる。
・増加や減少などの推移が近似している国がどことどこだか、わかりやすい。
ということが言えそうです。
上掲のFinancial Times掲載のチャートでは、点線の直線が書き込まれています。死亡者数が「毎日倍になる(Deaths Double Every Day)」「二日ごとに倍になる(... Every 2 Days)」「三日ごとに倍になる(... Every 3 Days)」「毎週倍になる(... Every Week)」それぞれのシナリオ別の増減が点線の直線で示されており、指数関数的増加を危機の前提としたとき、各国の変化量がどの程度なのか、もしくはどこととこの国が似ているのかが、点線の直線を参考にしながら理解することが可能となります。これが線形スケールの場合、増減の変化が直線ではなく、曲線を頭の中で描くことは難しいでしょう。
New York Timesでも、州ごとの状況を示す、表示方法を真似たものが、のちに登場しました。
Coronavirus Deaths by U.S. State and Country Over Time: Daily Tracker

カレンダー・ヒートマップ形式
必ずしも折れ線グラフのみではなく、カレンダー・ヒートマップ形式で示す例もありました。こちらも対数スケールで、今回は色で表現されています。折れ線グラフと比べると、指数関数的増減はわかりづらいですが、国間で広がり始めたタイミングやどういった変化量なのかが概観できますね。
Coronavirus Map: Tracking the Global Outbreak - The New York Times

両対数スケールにて、確定症例数の指数関数的変化を知りたい
上掲の片対数ではなく、両対数(両軸が対数スケール)を用いたチャートが登場し、わかりやすいと話題になっています。
片軸が時間軸ではなく、両軸ともに感染者のステータス(新規症例数と累積症例数)を示していることで、これまで(筆者がみた限り)どのメディアでも掲載していなかった形式のチャートだと思います。
実際の動画を見ていただければと思いますが、指数関数的に感染者が増え続ける国は直線に進みつづけ、収束に向かいつつある国(中国や韓国)は直線を離脱し、真下へ移動しています。
動画から該当部分を引用します(翻訳は筆者)。
このグラフの背後にある3つ目のアイデアは物理学からのものです:時間に対してプロットしないことです。通常、指数関数的な成長を見るとき、時間に対して症例数がプロットされます。しかし、病気の蔓延は3月か4月かを気にしません:ただ2つのことを気にしています:現在の症例数と、新しい症例がどれだけ増えるか、つまり成長率です。
指数関数的成長の特徴は、新規症例数が既存症例数に比例するということです。つまり、新規症例数と累積症例数をプロットすると、指数関数的な成長が直線として現れます。
これは、すべての国がCOVID-19の旅の中でどこにいるのかを示す、美しくも恐ろしいグラフを提供してくれます。そして、検査、隔離、社会的距離、コンタクト・トレーシングのような公衆衛生上の対策が、どこでこの病気を撃退し始めたのか、どこで効果がないのか、あるいはデータに現れるまでに時間がなかったのかを明らかにしています。ほぼ全ての国(※今のところ)で、そうでなくなるまで、ほぼ同じようなペースで症例数が増えています。
そして、それは、私がこれほど多くのCOVID-19の報道から欠けているように感じるものです:私達がトンネルの終わりに光を見ることができるかどうかの感覚。私たちはまだ伝染病のロケット船に乗っているのでしょうか、それとも緊急脱出ボタンを押すことができたのでしょうか?このグラフは、この不確実な時代に実際に何が起こっているのか、ある程度の感覚を与えてくれます。そうは言っても、このグラフはまた、いくつかの注意点&制限があり、その主な目的は、指数関数的成長からの逸脱を強調することです - つまり、トンネルの終わりの光を増幅することです。そのため、他の目的ではあまり参考にならないかもしれません。
動画の方では英語ナレーション(日本語字幕あり)を用いて説明しており、理解が深まると思いますので、そちらをご覧ください。ただし作者は疫学の専門家ではない、とのことです。
線形スケールのエリアチャートにて、感染者とその内訳(治癒者、死者、治療中etc)の推移を知りたい
感染者とその内訳(治癒者、死者、治療中etc)を時系列チャートで示す場合、横軸が各国比較をしないのであれば時系列(実際の日付)、縦軸は線形スケールを用いて、エリアチャートで表現している例が多いです。指数関数的増加のみに注目するのではなく、ステータスの内訳に注目するということと、折れ線グラフよりもエリアチャートの方が、内訳の時系列変化を把握しやすいからでしょう。
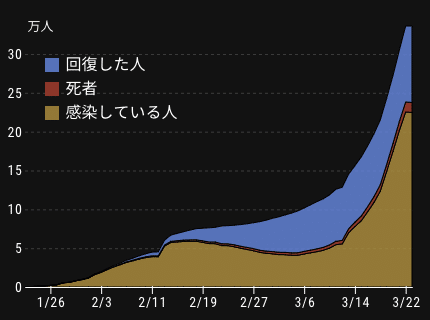
日経新聞(対象:全世界)
新型コロナウイルス感染 世界マップ:日本経済新聞
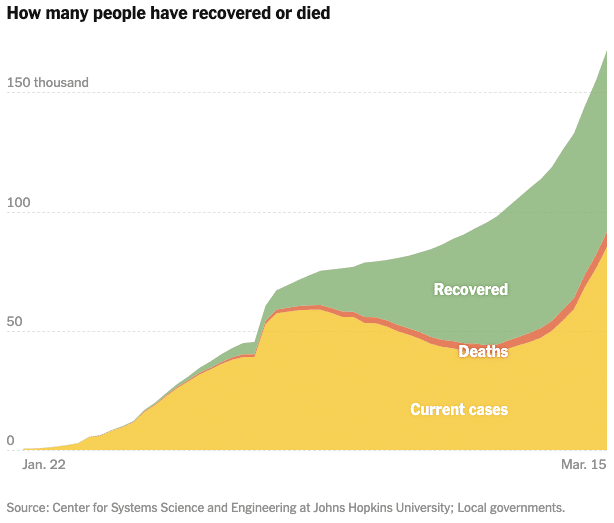
ニューヨーク・タイムズ(対象:全世界)
Coronavirus Map: Tracking the Global Outbreak - The New York Times
ロイター(対象:全世界)
Map and charts showing the spread of the novel coronavirus

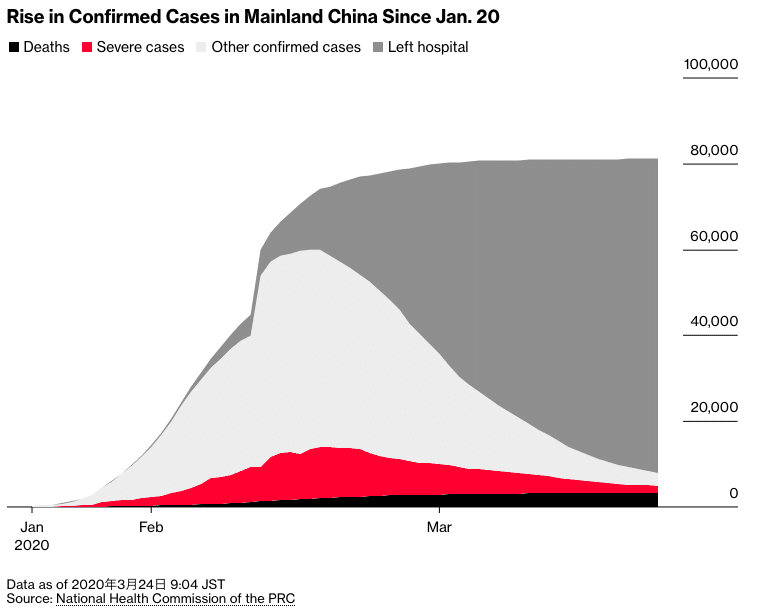
ブルームバーグ(中国のみ)
What Is Coronavirus: Mapping the Pneumonia-Like Respiratory Illness in China, Globally
ダッシュボードで何を伝えるべきか
毎日ダッシュボードの数値がアップデートされることは非常にありがたいですが、英語でいうとコール・トゥ・アクション、日本語で言うと「それで?」に答えるものとして、漫然と数値を表示するよりは、
・片対数スケール + 時系列、もしくは両対数スケールにて、確定症例数の指数関数的推移を知る。知ることで、感染者数が指数関数的に増加していないかどうか、NPI(ワクチンがまだ存在しない中、ソーシャル・ディスタンシングを含む、医療品以外の公衆衛生上の対策)などが上手くいっているかどうか、(発症のタイムラグはありますが)今、自国や自分の地域がどのような状況に置かれているのかを知りたい。
・線形スケールのエリアチャートにて、感染者とその内訳(治癒者、死者、治療中etc)の推移を示し、亡くなった方が何名いて、治癒した方が何名いて、という被害状況を実数(実際の人数)で把握したい。
というニーズに答える整理の仕方もありそうです。

