深層学習1ｄａｙレポート

〚内容〛

この回では主に、入力から出力し答え合わせをして、その誤差を確認。誤差を正解に近づけるためバイアスを調整する。バイアスを調整する為に誤差逆伝搬法を使ってバイアスを計算する流れ。

Section1：入力層〜中間層

【解説】

入力層から中間層の構造、図にすると下記の通り

力層から中間層の構造、式にすると下記の通り

入力内容Xの例：猫、犬、猿等を分類する時、それを判断する為の材料がXとなる。色ラベル、髭の長さ耳の長さ、重量、大きさ、の数値が判断材料となる。

【実装/演習】

from google.colab import drive
drive.mount('/content/drive')
import sys
sys.path.append('/content/drive/My Drive/DNN_code_colab_lesson_1_2')

goolgeドライブになんという名前で保存したのか確認してください。

僕の場合は　DNN_code_colab_lesson_1_2　にて保存しました。

そうしないと以降

from common import functionsが

が動きません。

どうしても意味が分からない時は　関数を作る。

def relu(x):
 return np.maximum(0, x)
 

def init_network():
   print("##### ネットワークの初期化 #####")
   network = {}
   
   network['W1'] = np.array([
       [0.1, 0.3, 0.5],
       [0.2, 0.4, 0.6]
   ])
   network['W2'] = np.array([
       [0.1, 0.4],
       [0.2, 0.5],
       [0.3, 0.6]
   ])
   network['W3'] = np.array([
       [0.1, 0.3],
       [0.2, 0.4]
   ])
   network['b1'] = np.array([0.1, 0.2, 0.3])
   network['b2'] = np.array([0.1, 0.2])
   network['b3'] = np.array([1, 2])
   print_vec("重み1", network['W1'] )
   print_vec("重み2", network['W2'] )
   print_vec("重み3", network['W3'] )
   print_vec("バイアス1", network['b1'] )
   print_vec("バイアス2", network['b2'] )
   print_vec("バイアス3", network['b3'] )
   return network
# プロセスを作成
# x：入力値
def forward(network, x):
   
   print("##### 順伝播開始 #####")
   W1, W2, W3 = network['W1'], network['W2'], network['W3']
   b1, b2, b3 = network['b1'], network['b2'], network['b3']
   
   # 1層の総入力
   u1 = np.dot(x, W1) + b1
   
   # 1層の総出力
   z1 = relu(u1)
   
   # 2層の総入力
   u2 = np.dot(z1, W2) + b2
   
   # 2層の総出力
   z2 = relu(u2)
   # 出力層の総入力
   u3 = np.dot(z2, W3) + b3
   
   # 出力層の総出力
   y = u3
   
   print_vec("総入力1", u1)
   print_vec("中間層出力1", z1)
   print_vec("総入力2", u2)
   print_vec("出力1", z1)
   print("出力合計: " + str(np.sum(z1)))
   return y, z1, z2
# 入力値
x = np.array([1., 2.])
print_vec("入力", x)
# ネットワークの初期化
network =  init_network()
y, z1, z2 = forward(network, x)

【確認テスト/考察結果】

：問に対する考察

この場合、ｗは何かと言うと重要度。例えば猫と犬を分類する時に、

世の中にこの「ねこ」と「いぬ」しかいなかった場合。目の数や鼻の数は同じ（ねこの中央のＶ字は鼻）なので重要度が少ないと思われるし、毛の色の重要度ｗは大きくなる。違いの情報が大きいものは情報が多いｗが多いと認識すると分かりやすいと思われる。

【関連/図書・問題・記事】

この入力層中間層の関係は簡単な論理回路を作ることも可能である。

この場合　

例えば重さとΘを設定して（Ｗ１,Ｗ２,Θ）を0.5，0.5，0.7に設定すれば正しい出力は可能。この考えが入力層中間層の構造の考え方にある。

[ゼロから作るDeapLearning]より

Section2：活性化関数

【解説】
関数は線形非線形に分けられる。

線形のものは

中間層:ステップ関数、Reru関数、シグモイド(ロジスティック)関数

出力層:恒等関数、シグモイド(ロジスティック)関数、ソフトマックス関数

【実装/演習】

import sys, os
import numpy as np

def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)
    print("shape: " + str(vec.shape))
    print("")

def relu(x):
　　return np.maximum(0, x)

# 順伝播（3層・複数ユニット）

# ウェイトとバイアスを設定
# ネートワークを作成
def init_network():
    print("##### ネットワークの初期化 #####")
    network = {}
    
    input_layer_size = 3
    hidden_layer_size_1=10
    hidden_layer_size_2=5
    output_layer_size = 4
    
    #試してみよう
    #_各パラメータのshapeを表示
    #_ネットワークの初期値ランダム生成
    network['W1'] = np.random.rand(input_layer_size, hidden_layer_size_1)
    network['W2'] = np.random.rand(hidden_layer_size_1,hidden_layer_size_2)
    network['W3'] = np.random.rand(hidden_layer_size_2,output_layer_size)

    network['b1'] =  np.random.rand(hidden_layer_size_1)
    network['b2'] =  np.random.rand(hidden_layer_size_2)
    network['b3'] =  np.random.rand(output_layer_size)

    print_vec("重み1", network['W1'] )
    print_vec("重み2", network['W2'] )
    print_vec("重み3", network['W3'] )
    print_vec("バイアス1", network['b1'] )
    print_vec("バイアス2", network['b2'] )
    print_vec("バイアス3", network['b3'] )

    return network

# プロセスを作成
# x：入力値
def forward(network, x):
    
    print("##### 順伝播開始 #####")

    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    # 1層の総入力
    u1 = np.dot(x, W1) + b1
    
    # 1層の総出力
    z1 = relu(u1)
    
    # 2層の総入力
    u2 = np.dot(z1, W2) + b2
    
    # 2層の総出力
    z2 = relu(u2)

    # 出力層の総入力
    u3 = np.dot(z2, W3) + b3
    
    # 出力層の総出力

    y = u3
    
    print_vec("総入力1", u1)
    print_vec("中間層出力1", z1)
    print_vec("中間層出力2", z2)
    print_vec("総入力2", u2)
    print_vec("出力", y)
    print("出力合計: " + str(np.sum(y)))

    return y, z1, z2

# 入力値
x = np.array([1., 2., 4.])
print_vec("入力", x)

# ネットワークの初期化
network =  init_network()

y, z1, z2 = forward(network, x)

※relu()関数は実際にコードを打ってみました。

【確認テスト/考察結果】

：問に対する考察

このページの中で、関数の何を使うかは読めないが、関数を使って値が処理されている事は理解ができる。

回答は

となるが、実際の動きはここでは分からない。

cmmonfileの中のReru関数を確認

この処理がされている。

【関連/図書・問題・記事】

勾配消失問題とは何か。

シグモイド関数導関数の値を入力変数に関してプロットしてみると，下記のようになる。

上図中央下の導関数の形を見ると、入力が原点から遠くなるにつれ勾配の値がどんどん減少し、0に漸近していくことが見て取れる。

これは、更新量を求めるには、そのパラメータよりも先の全ての関数の勾配を掛け合わせる必要がある。

このとき、活性化関数にシグモイド関数を用いていると小数点をかけていくことになり、繰り返し掛け合わされることになるため、入力に近い層に流れていく勾配がどんどん0に近づいていってしまう。

結果何も判断できない、という問題のことを言う。

現在それをカバーしたRelu関数が用いられることが多くなった。

[関連記事より抜粋]

Section3：出力層

【解説】

出力層とは、結果。人が欲しい答えを出力する層のことを言う。数字だったり、分類だったり、分類でも何割の確率の分類等。

それ等を出力する層となっている。

出力に使用される関数:

学習の流れ:

訓練データを元に出力する↓

ラベルと比べる↓

正誤をどのように合っていたか確認する↓

その誤差を誤差関数により、算出する。

誤差関数に使われる関数:クロスエントロピー誤差、二乗平均誤差がよく使われている。

【実装/演習】

import numpy as np

# 中間層の活性化関数
# シグモイド関数（ロジスティック関数）
def sigmoid(x):
    return 1/(1 + np.exp(-x))

# ReLU関数
def relu(x):
    return np.maximum(0, x)

# ステップ関数（閾値0）
def step_function(x):
    return np.where( x > 0, 1, 0) 

# 出力層の活性化関数
# ソフトマックス関数
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

# ソフトマックスとクロスエントロピーの複合関数
def softmax_with_loss(d, x):
    y = softmax(x)
    return cross_entropy_error(d, y)

# 誤差関数
# 平均二乗誤差
def mean_squared_error(d, y):
    return np.mean(np.square(d - y)) / 2

# クロスエントロピー
def cross_entropy_error(d, y):
    if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size



# 活性化関数の導関数
# シグモイド関数（ロジスティック関数）の導関数
def d_sigmoid(x):
    dx = (1.0 - sigmoid(x)) * sigmoid(x)
    return dx

# ReLU関数の導関数
def d_relu(x):
    return np.where( x > 0, 1, 0)
    
# ステップ関数の導関数
def d_step_function(x):
    return 0

# 平均二乗誤差の導関数
def d_mean_squared_error(d, y):
    if type(d) == np.ndarray:
        batch_size = d.shape[0]
        dx = (y - d)/batch_size
    else:
        dx = y - d
    return dx


# ソフトマックスとクロスエントロピーの複合導関数
def d_softmax_with_loss(d, y):
    batch_size = d.shape[0]
    if d.size == y.size: # 教師データがone-hot-vectorの場合
        dx = (y - d) / batch_size
    else:
        dx = y.copy()
        dx[np.arange(batch_size), d] -= 1
        dx = dx / batch_size
    return dx

# シグモイドとクロスエントロピーの複合導関数
def d_sigmoid_with_loss(d, y):
    return y - d

# 数値微分
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        # f(x + h)の計算
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x - h)の計算
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2 * h)
        # 値を元に戻す
        x[idx] = tmp_val

    return grad


def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    N, C, H, W = input_data.shape
    out_h = (H + 2*pad - filter_h)//stride + 1
    out_w = (W + 2*pad - filter_w)//stride + 1

    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
    return col


def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    N, C, H, W = input_shape
    out_h = (H + 2*pad - filter_h)//stride + 1
    out_w = (W + 2*pad - filter_w)//stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

    img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]

※他の関数も中身の確認

# 多クラス分類
# 3-2-3ネットワーク

# ネートワークを作成
def init_network():
    print("##### ネットワークの初期化 #####")

   

    network = {}
    
    input_layer_size = 3
    hidden_layer_size=2
    output_layer_size = 3
    
 
    network['W1'] = np.random.rand(input_layer_size, hidden_layer_size)
    network['W2'] = np.random.rand(hidden_layer_size,output_layer_size)

    network['b1'] =  np.random.rand(hidden_layer_size)
    network['b2'] =  np.random.rand(output_layer_size)
    
    print_vec("重み1", network['W1'] )
    print_vec("重み2", network['W2'] )
    print_vec("バイアス1", network['b1'] )
    print_vec("バイアス2", network['b2'] )

    return network

# プロセスを作成
# x：入力値
def forward(network, x):
    
    print("##### 順伝播開始 #####")
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    
    # 1層の総入力
    u1 = np.dot(x, W1) + b1

    # 1層の総出力
    z1 = relu(u1)

    # 2層の総入力
    u2 = np.dot(z1, W2) + b2
    
    # 出力値
    y = softmax(u2)
    
    print_vec("総入力1", u1)
    print_vec("中間層出力1", z1)
    print_vec("総入力2", u2)
    print_vec("出力1", y)
    print("出力合計: " + str(np.sum(y)))
        
    return y, z1

## 事前データ
# 入力値
x = np.array([1., 2.,  3.])

# 目標出力
d = np.array([0, 0, 0, 1, 0, 0])

# ネットワークの初期化
network =  init_network()

# 出力
y, z1 = forward(network, x)

# 誤差
loss = cross_entropy_error(d, y)

## 表示
print("\n##### 結果表示 #####")
print_vec("出力", y)
print_vec("訓練データ", d)
print_vec("誤差",  loss)

【確認テスト/考察結果】

：問に対する考察

１つのデータが一体どれだけ、ズレがあるのかを見るのに、合計をして見るが、その差がマイナスもプラスもあり、合計されるだけでは相殺される為

特徴を出して尚且符号のマイナスを無くすためニ乗がある。

1/2はどういう意味か:

最小勾配法で2乗和誤差を微分する際に、降りてきた指数2と打ち消しって消えてくれるよう1/2を掛けている。 

鞍点を求めるにあたっては、係数が何であろうと計算結果に影響は与えない。 なので数学的な慣習として1/2を付けている。

【関連/図書・問題・記事】

ソフトマックス関数:

ソフトマックス関数とは、分類問題で使用される。

ソフトマックス関数は0から1の間で出力され、出力の総和が1となる。

つまり確率とみなすことができる。

●出力例

猫の分類として結果、猫、犬、トラ3出力あるとしてソフトマックス関数なしの場合。

400％中、猫が200％、犬が150％、トラが50％と言えて、内容が分かりにくい。

ソフトマックス関数ありの場合

合計が1となり、確率が把握しやすい。

[いくつかの関連記事よりまとめ]

Section4：勾配降下法

【解説】

勾配降下法の種類:勾配降下法、確率的勾配降下法、ミニバッチ勾配降下法がある。

勾配降下法:

勾配降下法問題点

学習率の大きさにより正しく収束しないという問題が起きる。

●大きい場合には発散し収束しない。

●小さい場合は発散はしないが、収束まで時間がかかったり、正しい収束点ではないところで計算が終わる可能性がある。

確率的勾配降下法(SGD):

勾配降下法との違いは、誤差の出し方の違い。確率的勾配降下法はランダムに抽出した誤差を使用する。

確率的勾配降下法のメリット

●データが多いときのコストの削減

●望まない局所極小解を回避する

●オンライン学習が出来る。

ミニバッチ勾配降下法:

ミニバッチ勾配降下法のメリット:

●ミニバッチ勾配降下には計算機の計算資源を有効利用できるメリットがある

【実装/演習】

確率勾配降下法

# coding: utf-8

# In[ ]:


# 確率勾配降下法
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np

import matplotlib.pyplot as plt

def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)
    #print("shape: " + str(x.shape))
    print("")


# In[ ]:


# サンプルとする関数 #yの値を予想するAI 

def f(x):
    y = 3 * x[0] + 2 * x[1]
    return y

# 初期設定
def init_network():
    #print("##### ネットワークの初期化 #####")
    network = {}
    nodesNum = 10
    network['W1'] = np.random.randn(2, nodesNum)
    network['W2'] = np.random.randn(nodesNum)
    network['b1'] = np.random.randn(nodesNum)
    network['b2'] = np.random.randn()

    #print_vec("重み1", network['W1'])
    #print_vec("重み2", network['W2'])
    #print_vec("バイアス1", network['b1'])
    #print_vec("バイアス2", network['b2'])

    return network

# 順伝播
def forward(network, x):
    #print("##### 順伝播開始 #####")
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    u1 = np.dot(x, W1) + b1
    z1 =relu(u1)
    
    ## 試してみよう
    z1 = sigmoid(u1)
    
    u2 = np.dot(z1, W2) + b2
    y = u2

    #print_vec("総入力1", u1)
    #print_vec("中間層出力1", z1)
    #print_vec("総入力2", u2)
    #print_vec("出力1", y)
    #print("出力合計: " + str(np.sum(y)))    
    
    return z1, y

# 誤差逆伝播
def backward(x, d, z1, y):
    print("\n##### 誤差逆伝播開始 #####")    

    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ
    delta2 = d_mean_squared_error(d, y)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 中間層でのデルタ
    #delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)

    ## 試してみよう
    delta1 = np.dot(delta2, W2.T) * d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
    
    print_vec("偏微分_重み1", grad["W1"])
    print_vec("偏微分_重み2", grad["W2"])
    print_vec("偏微分_バイアス1", grad["b1"])
    print_vec("偏微分_バイアス2", grad["b2"])

    return grad

# サンプルデータを作成
data_sets_size = 100
data_sets = [0 for i in range(data_sets_size)]

for i in range(data_sets_size):
    data_sets[i] = {}
    # ランダムな値を設定
    data_sets[i]['x'] = np.random.rand(2)
    
    ## 試してみよう_入力値の設定
    # data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
    
    # 目標出力を設定
    data_sets[i]['d'] = f(data_sets[i]['x'])
    
losses = []
# 学習率
learning_rate = 0.07

# 抽出数
epoch = 100

# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)

# 勾配降下の繰り返し
for dataset in random_datasets:
    x, d = dataset['x'], dataset['d']
    z1, y = forward(network, x)
    grad = backward(x, d, z1, y)
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'b1', 'b2'):
        network[key]  -= learning_rate * grad[key]

    # 誤差
    loss = mean_squared_error(d, y)
    losses.append(loss)

print("##### 結果表示 #####")    
lists = range(epoch)


plt.plot(lists, losses, '.')
# グラフの表示
plt.show()

※出力結果は項目が多いので一部抜粋。

【確認テスト/考察結果】

オンライン学習はデータをランダムに1件ずつ投入してモデルを更新していく手法。

オンライン学習のメリット

●1件ずつデータを投入するためメモリ使用量も少なく、モデル学習にかかる計算負荷も小さい。

●バッチ学習が不得意とするリアルタイムでモデル更新を頻繁に行うケースにも適用しやすい。

【関連/図書・問題・記事】

勾配法：

f(x0,X)1 = x0^2+x1^2 の最小値を勾配法で求める。

import numpy as np

def numerical_gradient(f,x):
 h = 1e-4
 grad = np.zeros_like(x)
 for idx in range(x.size):
   tmp_val =x[idx]
   x[idx] = tmp_val+h
   fxh1 = f(x)
   x[idx] =tmp_val -h
   fxh2 = f(x)
   
   grad[idx] = (fxh1 - fxh2) / (2*h)
   x[idx] = tmp_val
 return grad

def gradient_descent(f,init_x,lr = 0.01,strp_num = 100):
 x = init_x
 for i in range(strp_num):
   grad = numerical_gradient(f,x)
   x -= lr * grad
 return x
 #f (x0,X)1 = x0^2+x1^2 の最小値を勾配法で求める。
def function_2(x):
 return x[0]**2 + x[1]**2



init_x =np.array([-3.0,4.0])

gradient_descent(function_2,init_x=init_x,lr=0.1,strp_num = 100)

[関連記事より抜粋]

Section5：誤差逆伝搬法

【解説】

算出された誤差を出力層から順に微分し、前の層へと伝搬し最小限の計算でパラメータの微分を解析的に、計算する手法。

この図は、逆伝播により同じ式を繰り返し使うことが出来ることを示している。

【実装/演習】

import sys
sys.path.append('/content/drive/My Drive/DNN_code_colab_lesson_1_2')

import numpy as np
from common import functions
import matplotlib.pyplot as plt
def print_vec(text, vec):
   print("*** " + text + " ***")
   print(vec)
   #print ("shape: " + str(x.shape))
   print("")

 #ウェイトとバイアスを設定 
# ネートワークを作成
def init_network():
   print("##### ネットワークの初期化 #####")
   network = {}
   network['W1'] = np.array([
       [0.1, 0.3, 0.5],
       [0.2, 0.4, 0.6]
   ])
   network['W2'] = np.array([
       [0.1, 0.4],
       [0.2, 0.5],
       [0.3, 0.6]
   ])
   network['b1'] = np.array([0.1, 0.2, 0.3])
   network['b2'] = np.array([0.1, 0.2])
   
   print_vec("重み1", network['W1'])
   print_vec("重み2", network['W2'])
   print_vec("バイアス1", network['b1'])
   print_vec("バイアス2", network['b2'])
   return network
# 順伝播
def forward(network, x):
   print("##### 順伝播開始 #####")
   W1, W2 = network['W1'], network['W2']
   b1, b2 = network['b1'], network['b2']
   
   u1 = np.dot(x, W1) + b1
   z1 = functions.relu(u1)
   u2 = np.dot(z1, W2) + b2
   y = functions.softmax(u2)
   
   print_vec("総入力1", u1)
   print_vec("中間層出力1", z1)
   print_vec("総入力2", u2)
   print_vec("出力1", y)
   print("出力合計: " + str(np.sum(y)))
   return y, z1
# 誤差逆伝播
def backward(x, d, z1, y):
   print("\n##### 誤差逆伝播開始 #####")
   grad = {}
   W1, W2 = network['W1'], network['W2']
   b1, b2 = network['b1'], network['b2']
   #  出力層でのデルタ
   delta2 = functions.d_sigmoid_with_loss(d, y)
   #  b2の勾配
   grad['b2'] = np.sum(delta2, axis=0)
   #  W2の勾配
   grad['W2'] = np.dot(z1.T, delta2)
   #  中間層でのデルタ
   delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
   # b1の勾配
   grad['b1'] = np.sum(delta1, axis=0)
   #  W1の勾配
   grad['W1'] = np.dot(x.T, delta1)
       
   print_vec("偏微分_dE/du2", delta2)
   print_vec("偏微分_dE/du2", delta1)
   print_vec("偏微分_重み1", grad["W1"])
   print_vec("偏微分_重み2", grad["W2"])
   print_vec("偏微分_バイアス1", grad["b1"])
   print_vec("偏微分_バイアス2", grad["b2"])
   return grad
   
# 訓練データ
x = np.array([[1.0, 5.0]])
# 目標出力
d = np.array([[0, 1]])
#  学習率
learning_rate = 0.01
network =  init_network()
y, z1 = forward(network, x)
# 誤差
loss = functions.cross_entropy_error(d, y)
grad = backward(x, d, z1, y)
for key in ('W1', 'W2', 'b1', 'b2'):
   network[key]  -= learning_rate * grad[key]
print("##### 結果表示 #####")    

print("##### 更新後パラメータ #####") 
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])

【確認テスト/考察結果】

確率的勾配降下法の中にある誤差逆伝播法のコードより確認。

【関連/図書・問題・記事】

誤差逆伝播法図解:

この様に、出力まで計算が進んみ(順伝播)出力から誤差を計算し、誤差を調整する為に入力に向かって計算されることを「誤差逆伝播」と言う。

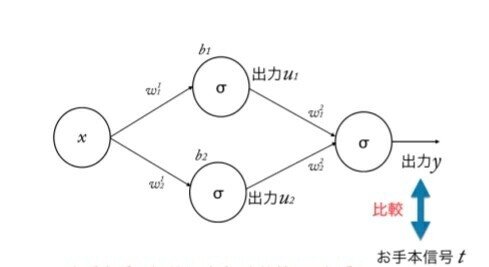
比較する時は、差を考えればいいが、マイナスやプラスが考えられるので、計算しやすくするために、差の二乗を考える。

 ○誤差Eを，E=(y−t)2と定義したい

○目的は、重みwや、バイアス

bを変化させることで出力信号と

お手本信号の誤差をなくすこと

○つまり重みwや、バイアスwの変

化による、誤差Eの変化量が大事

○変化量といえば… 微分ということで
Eを微分することが多いので、
E=1/2(y−t)2と定義しておく


○E=1/2(y−t)2を0にする

ように重みwや、バイアスbを修正していく

このようなプロセスが一連の流れとなっている。

[関連記事より抜粋]