
深層学習2dayレポート
[内容]
今回は、ニューラルネットワークでのいくつかの注意点と、代表的なアルゴリズムの考え方を学ぶ。
Section1:勾配消失問題
【解説】
勾配消失問題とは、下位層に誤差逆伝搬法が進んでいく時に勾配がなだらかになり、更新がほとんど変わらない、最適化にならず収束しない現象のことである。

※横が学習回数、縦がtraining と test の正解率。本来は右のように学習を重ねれば正解率が上がるが勾配消失問題が起きると左の図のように正解率が上がらない現象が起きる。
勾配消失問題の解決法3つ
●活性化関数の選択
活性化関数が理由で勾配消失問題を引き起こすものがシグモイド関数。誤差逆伝搬法を使用する時、微分の連鎖にて微分するが、シグモイド関数を最大が0.25となる。
微分の連鎖率は、微分の掛け算により計算していく中で層が多くなればなる程0.25の掛け算が多くなり、重みの変化が伝わらなくなり学習率が上がらない。
改善方法として、Relu関数を使う方法が有る。
def der_relu(x):
return 1.0 * (x > 0.0)
●重みの初期値の設定
w重みは乱数によって設定される。勾配消失問題を改善できる乱数の設定方法がいくつかある。
・wの重みの設定
:標準正規分布
自然界に多い分布だが、出力が0か1に偏るので情報量が多い分散状態からは遠い

:標準正規分布を小さな値で割ってみる
極端に中央に偏る分布になる。情報量が多い分散状態から遠い。

:Xavierで設定してみる
ちょうどよく分散している事が分かる。


※S字カーブの分布の関数、シグモイド関数などにいい感じに働く。S字カーブではないものに関してはHeと言う初期値設定がよく働く。
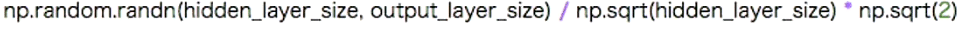
標準偏差√(n/2)で割る方法がある。
●バッチ処理化
大量のデータを分割し処理する。※バッチ処理と言う。
・学習を早く進行させられる。
・過学習を抑制する。
勾配消失問題の改善としては?
多分、バッチ化することで1回で処理する層が浅くすることが出来るのでシグモイド関数部分を多く掛け算する必要がなくなるから?
【実装/演習】
※Googleドライブのマウント抜粋
import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10
# 初期設定
def init_network():
network = {}
network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)
network['b1'] = np.zeros(hidden_layer_1_size)
network['b2'] = np.zeros(hidden_layer_2_size)
network['b3'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_f = functions.sigmoid
u1 = np.dot(x, W1) + b1
z1 = hidden_f(u1)
u2 = np.dot(z1, W2) + b2
z2 = hidden_f(u2)
u3 = np.dot(z2, W3) + b3
y = functions.softmax(u3)
return z1, z2, y
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_d_f = functions.d_sigmoid
last_d_f = functions.d_softmax_with_loss
# 出力層でのデルタ
delta3 = last_d_f(d, y)
# b3の勾配
grad['b3'] = np.sum(delta3, axis=0)
# W3の勾配
grad['W3'] = np.dot(z2.T, delta3)
# 2層でのデルタ
delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, z2, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1 : d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, z2, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, z2, y)
if (i+1)%plot_interval==0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
上限2000回まで学習しているが、正解率が向上しない。
Relu関数に変えた場合の学習率

シグモイド関数にXavierを使った場合の学習率
import numpy as np
from data.mnist import load_mnist
from PIL import Image
import pickle
from common import functions
import matplotlib.pyplot as plt
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10
# 初期設定
def init_network():
network = {}
########### 変更箇所 ##############
# Xavierの初期値
network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / (np.sqrt(input_layer_size))
network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / (np.sqrt(hidden_layer_1_size))
network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / (np.sqrt(hidden_layer_2_size))
#################################
network['b1'] = np.zeros(hidden_layer_1_size)
network['b2'] = np.zeros(hidden_layer_2_size)
network['b3'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_f = functions.sigmoid
u1 = np.dot(x, W1) + b1
z1 = hidden_f(u1)
u2 = np.dot(z1, W2) + b2
z2 = hidden_f(u2)
u3 = np.dot(z2, W3) + b3
y = functions.softmax(u3)
return z1, z2, y
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_d_f = functions.d_sigmoid
# 出力層でのデルタ
delta3 = functions.d_softmax_with_loss(d, y)
# b3の勾配
grad['b3'] = np.sum(delta3, axis=0)
# W3の勾配
grad['W3'] = np.dot(z2.T, delta3)
# 2層でのデルタ
delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)Section3:過学習
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, z2, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1 : d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, z2, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, z2, y)
if (i+1)%plot_interval==0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
学習率の向上が分かる。
ReLU関数を使った時 He処理をした場合。

この場合も学習率が向上していることが分かる。
【確認テスト/考察結果】

考察:シグモイド関数の微分がなぜ0.25なのか。


シグモイド関数の微分はものすごく難しいけれど、結果はかなりシンプルなものになっている。これを実際に計算すると
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10)
#シグモイド関数
y = sigmoid(x)
plt.plot(x, y)
#シグモイド関数の微分
dy = (1 - sigmoid(x)) * sigmoid(x)
plt.plot(x, dy)
plt.show()
微分の最大値が0.25である事が分かる。
【関連/図書・問題・記事】
●重みの初期値を0にした場合どうなるか
重みを小さくすると、過学習が抑えられるメリットがある。小さくするということで0からスタートするとどうなるかと考える。
0にするということはまず、重みが均一になると言うこと。
仮に2層ネットワークが有るとして
1層目2層目の重みが0とすると、逆伝搬の時に2層目の重みが同じように更新されるということになる。
結果、重みが重複した値、対象な値となる。重みが均一になると沢山の重みを持つ意味がなくなる。
結論:
対象な重みを崩すためにランダムな初期設定が必要となる。
[ゼロから作るDeep Leaningより]
Section2:学習率最適化手法
【解説】
学習率最適化。学習率とはどこで使用したかと言うと、勾配降下法で使用した。

ξが学習率。この学習率が大きすぎると、収束されず、小さすぎると局所解で探索がとまったり、解までたどり着く時間がかかりすぎたりするというデメリットがある。
学習率最適化する手段:
•モメンタム:数式とコード

前回の重みを使用する。
•AdaGrad:数式とコード

なだらかな面でも解を求められるが、鞍点問題をおこすと言うデメリットがある。
•RMSProp:数式とコード

AdaGradと同じ動きをしがちであるがAdaGradと比較して局所解で止まりにくくなっている。加えて、シビアなハイパーパラメータの調整が不要。
•Adam:数式とコード
もっともよく使われている最適化アルゴリズムの一つである.Adam も RMSprop の改良版であり, 勾配に関しても以前の情報を指数的減衰させながら伝える。

ここで,m^t,v^tm^t,v^tは勾配,二乗勾配の不偏推定量となるように調整したものである、ハイパーパラメータはη=0.001,ρ1=0.9,ρ2=0.999,ε=10−8η=0.001,ρ1=0.9,ρ2=0.999,ε=10−8で与えられることが多い。
【実装/演習】
●SGDにて学習:
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
今回はminstsではうまく学習できていないことが分かる。
●Adamにて学習:
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 400
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
beta1 = 0.9
beta2 = 0.999
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
m = {}
v = {}
learning_rate_t = learning_rate * np.sqrt(1.0 - beta2 ** (i + 1)) / (1.0 - beta1 ** (i + 1))
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
m[key] = np.zeros_like(network.params[key])
v[key] = np.zeros_like(network.params[key])
m[key] += (1 - beta1) * (grad[key] - m[key])
v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])
network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()学習400に設定を変更したが、それでも92%正解率を出している。

【確認テスト/考察結果】

モメンタム:前回の微分したものを使って今回の移動を求める。
AdaGrad:手動による学習率のチューニングが不要
RMSProp:現状自分の言葉で言うと、モメンタムを改良したものと解答できそう。
【関連/図書・問題・記事】

Adamのコードが上記に記載してあるが、キ、クに当てはまる記載は何か。
キ:
self.rho2*self.v[key]+(1-self.rho2)*(grads[key]**2)ク:
self.m[key] / (1 - self.rho1**self.iter)クラスの使い方も問われる問題となっています。
[ディープラーニングE資格問題集より]
Section3:過学習
【解説】
過学習が起きると、訓練データには強いが実際のデータに対して予測が弱くなる学習のことを言い、原因は自由度が高いことが原因であるとも言える。
学習させていくと、重みにばらつきが発生する。重みが大きい値は、学習において重要な値であり、重みが大きいと過学習が起こる。
対応作として正則化L1,L2とドロップアウトという手法が使われる。
正則化L1,L2:
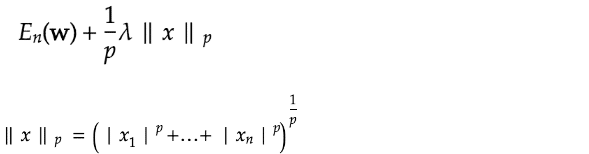
p = 1の場合、L1正則化と呼ぶ。
p = 2の場合、L2正則化と呼ぶ。

数式とコード:

ドロップアウト:

ランダムにノードを切断して学習させる手法となる。
【実装/演習】
L2ノルム:
from common import optimizer
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 400
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.1
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 400
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.005
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
【確認テスト/考察結果】

答えは3のnp.sign(praam)では有るが他のものについて説明をしてみたいと思う。
np.maximum(pram,0) はその最大の数値を出す関数
np.minimum(param,0)はその最小の数値を出す関数
np.sign(param)はその中で+、-の符号関数
np.abs(param)は配列要素の絶対値を取る
【関連/図書・問題・記事】

ア = L1ノルムはBで表され、イ = L2ノルムはEで表されられる。
L1ノルムは絶対誤差や特徴量にスパース性を誘導して特徴選択をしたい場合の正則化などに用いられる。
L2ノルムの2乗は二乗誤差や単にモデルが過剰に複雑になり過剰適合(過学習)を起こすことを避けるための正則化として用いられます。
ウは 最大値ノルムとも呼ばれています。
[ディープラーニングE資格問題集より]
Section4:畳み込みニューラルネットワークの概念
【解説】
画像の識別や画像の処理の為に使われるニューラルネットワーク。応用的に、次元の繋がりがあれば使用できる。
例えば、
(入力画像)畳み込み層→プーリング層→畳み込み層→畳み込み層→プーリング層→全結合層出力層→(出力画像)畳み込み層
という構造になる。
用語解説:
[畳み込み]
代表的なものにLeNetがある。

32×32の画像を10種類に分類する。
●畳み込み
畳み込み層では、画像の場合、縦、横、チャンネルの3次元のデータをそのまま学習し、次に伝えることができる。結論:3次元の空間情報も学習できるような層が畳み込み層である。
●フィルター
全結合でいう重み
●パディング

入力画像の辺に入力値を追加することで、画像のサイズを可変すること。
上記の表で周りをゼロで埋める場合 → ゼロパディングと呼ぶ。( 学習に影響を与えにくい )
●ストライド
フィルターで順次抽出する際の、 x および y に対する移動量をストライドという
●チャンネル
フィルターの数=チャンネル数
●プーリング層
重みがない処理をする。
マックスプーリング(MaxPooling)
畳み込み層の出力を入力とし、そのうちの最大値を出力する。
●アベレージプーリング(AvgPooling)
畳み込み層の出力を入力とし、それらの入力の平均値を出力する。
【実装/演習】
import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from common import optimizer
from data.mnist import load_mnist
import matplotlib.pyplot as plt
# 画像データを2次元配列に変換
'''
input_data: 入力値
filter_h: フィルターの高さ
filter_w: フィルターの横幅
stride: ストライド
pad: パディング
'''
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
# N: number, C: channel, H: height, W: width
N, C, H, W = input_data.shape
# 切り捨て除算
out_h = (H + 2 * pad - filter_h)//stride + 1
out_w = (W + 2 * pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3) # (N, C, filter_h, filter_w, out_h, out_w) -> (N, filter_w, out_h, out_w, C, filter_h)
col = col.reshape(N * out_h * out_w, -1)
return col# im2colの処理確認
input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す
print('========== input_data ===========\n', input_data)
print('==============================')
filter_h = 3
filter_w = 3
stride = 1
pad = 0
col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= col ==============\n', col)
print('==============================')
【確認テスト/考察結果】

手計算により理解を深める


【関連/図書・問題・記事】
全結合層の問題点:
全結合の問題点とは データの構造が"無視"されて、形状による情報を生かすことができない こと
形状には大切な情報が含まれていると思われるが、形状を無視して全てのデータを同じ次元のニューロンとして扱うので、形状による情報を生かすことができない。
例えば入力データが画像のとき、データは縦・横・チャンネル方向の3次元形状
MNIST データセットを使った例では、入力画像は (1, 28, 28)―― 1 チャンネル、縦 28 ピクセル、 横 28 ピクセル――の形状だったが、それを 1 列に並べた 784 個のデータを最初の Affine レイヤへ入力する
全結合層に入力するときに「3 次元のデータを平ら ―― 1 次元のデータ――にする」必要があるが、
平らにされて失うこの形状には大切な空間情報が含まれていると思われる。
空間的に近いピクセルは似たような値なのでは?
RBGの各チャンネルの間にはそれぞれに密接な関係があるのでは?
など...
CNN では、画像などの形状を有したデータを正しく理解できる(可能性がある)
CNNの畳み込み層において、
入出力データを特徴マップ(feature map)
入力データを入力特徴マップ(feature map)
出力データを出力特徴マップ(feature map)
[ゼロから作るDeepLearningより]
Section5:最新のCNN
【解説】
AlexNet
モデル構造、5層の畳み込み層及びプーリング層、等それに続く3層の結合層からなる。
過学習を防ぐ施策・サイズ4096の全結合層の出力にドロップアウトを使用している。

【関連/図書・問題・記事】
AlexNet
AlexNetは畳み込み層とプーリング層を重ねて、最後に全結合層を経由して結果を出力します。
LeNetとの以下の点が異なる
・活性化関数にReLU関数を用いる
・LRN(Local Response Normalization)と言う局所的正規化を行う層を用いる
・Dropoutを使用する
今と昔
ネットワーク構成にはLeNet、AlexNeには大きな違いはありませんが、コンピュータ技術に大きな進歩があった
具体的には
・大量のデータを誰でも入手できるようになった
・大量の並列計算を得意とするGPUが普及し、大量の演算を高速に行うことが可能になった。
[ゼロから作るDeepLearningより]
この記事が気に入ったらサポートをしてみませんか?
