みてわかる電子回路「小信号等価回路」

電子回路の勉強において最も理解に苦労するわりに、非常に重要な役割を果たす、小信号等価回路について解説をしてきます。長い記事となりますが、どうか最後までお付き合いください。
(ご利用にあたり免責事項をご一読ください)

例題その1

さて、いきなりですが、下図の例題に取り組んでみてください。

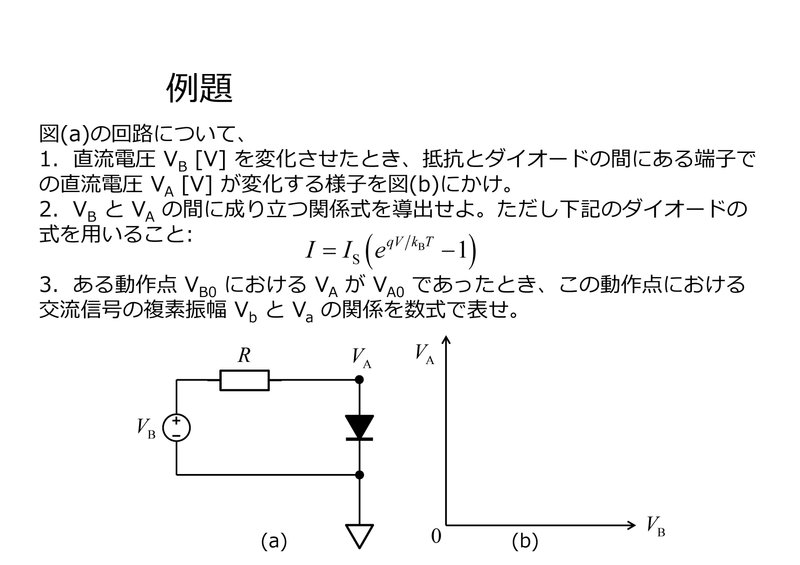
問1は既に以前解説済み（こちら）ですので、問2と問3から見ていきましょう。

問2の解は計算により
$${   V_{\rm{B}} = V_{\rm{A}} + R I_{\rm{S}} \left(  e^{q V_{\rm{A}} / k_{\rm{B}} T} -1 \right)  }$$
と書き表すことができます。
問3ではこの関係式を動作点の周りで微分することにより
$${ \frac{V_{\rm{a}}}{V_{\rm{b}}} = \left[ 1+\frac{q R I_{\rm{S}}}{k_{\rm{B}}T} e^{q V_{\rm{A, 0}}/k_{\rm{B}}T} \right]^{-1} }$$
としたものが解となります。
一般的には $${ V_{\rm{a}} }$$, $${ V_{\rm{b}} }$$ は複素数ですが、この回路では位相のズレが生じないため、特別に $${ V_{\rm{a}} }$$ も $${ V_{\rm{b}} }$$ も実数となります。

このように、いったん入力と出力の間の関係式を導出し、それを動作点の周辺で微分することで増幅率を計算するという方法は、考え方としては直接的で非常にわかりやすいですね。ところが、素子数が増え、トランジスターが素子として加わり、回路が少しでも複雑になると、このような入出力特性を数式で表すことが困難になるため、実践の場では現実的な方法であるとは言えません。

交流からみた入出力の関係

ここで、入力と出力の間の関係に着目してみましょう。
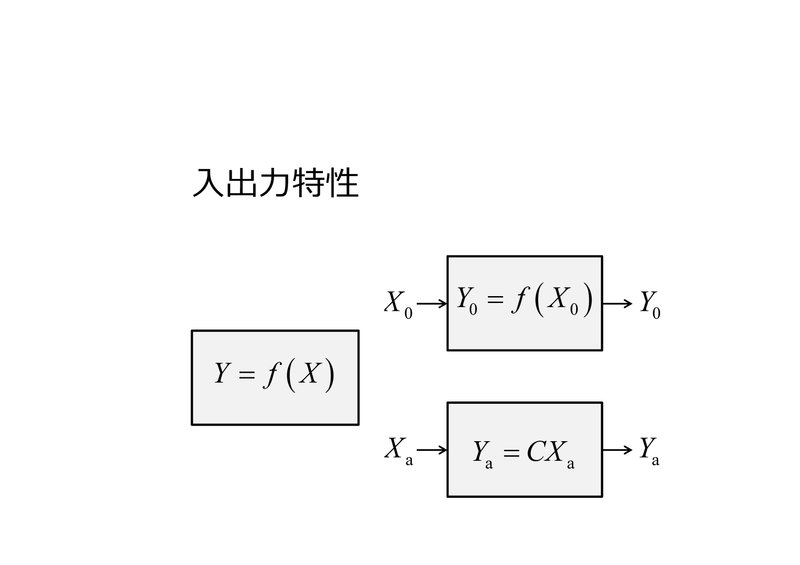
まず、入出力特性が関数 $${ f(X) }$$ で表される増幅器を考えます。この関数は一般的には非線形的で複雑なものかもしれません。
ところが、動作点 $${ X_{\rm{0}} }$$ 付近での微小な入力交流信号の複素振幅 $${ X_{\rm{a}} }$$ と 、それによる $${ Y_{\rm{0}} }$$ の周りの微小な出力交流信号の複素振幅 $${ Y_{\rm{a}} }$$ は、とても単純な比例関係 $${ Y_{\rm{a}} = C X_{\rm{a}} }$$ にあります。この比例係数 $${ C }$$ は動作点付近での入出力特性関数の微分によってあらわされ、$${ Y_{\rm{a}} }$$ および $${ X_{\rm{a}} }$$ によらない定数となります。このため、複素振幅の間の関係は常に線形な関係であることがわかります。

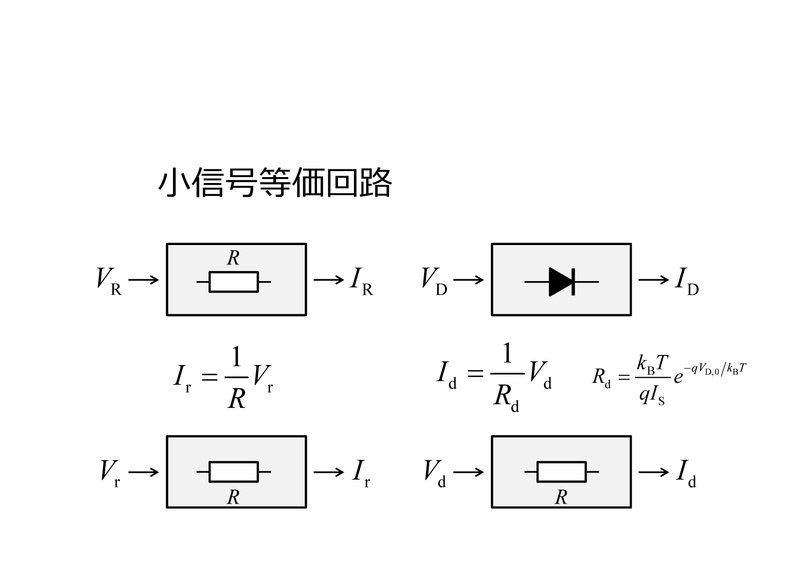
交流の目で見た抵抗

たとえば抵抗を例にとり、入力が電圧、出力が電流、という入出力特性を持つ電圧電流変換素子であるとみなしましょう。

まず直流的な入力電圧と直流的な出力電流の関係を表す静特性を見ると、入力として直流電圧 $${ V_{\rm{R}} }$$ が両端に印加されたときに出力として生じる直流電流は $${ I_{\rm{R}} = (1/R) V_{\rm{R}} }$$ となります。その関係は直線で表され、傾きは抵抗 $${ 1/R }$$ に等しくなります。オームの法則ですね。

次に交流的な複素振幅の入出力特性を考えましょう。動作点 $${ V_{\rm{R, 0}} }$$ の周りでの交流電圧信号（複素振幅 $${ V_{\rm{r}} }$$）を加えると、出力される交流電流信号の複素振幅は $${ I_{\rm{r}} = (1/R) V_{\rm{r}} }$$ となります。
つまり抵抗では、直流動作からみても交流信号からみても、入力電圧と出力電流は比例関係にあり、その比例係数は抵抗 $${ 1/R }$$ です。

別の言い方をすると、抵抗 $${ R }$$ は、直流から見ても交流から見ても抵抗だということですね。

交流の目で見たダイオード

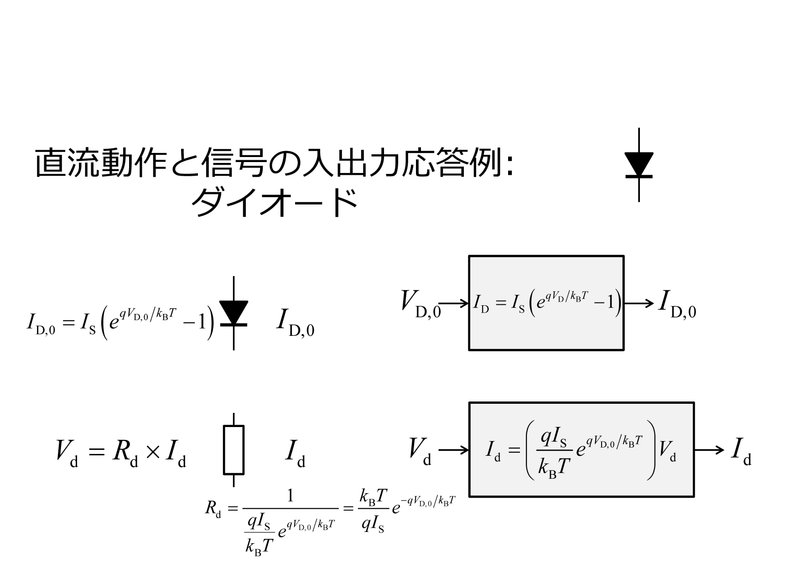
つぎに、PN接合ダイオードを、入力がダイオード両端の電位差、出力がダイオードに生じる電流量、という入出力特性を持つ電圧・電流変換素子であるとみなしましょう。

まず入力として直流電圧が順方向バイアスの向きに印加されたとき、ダイオードには指数関数的な電流が生じ、これを出力電流とみなすことができます。このとき入力と出力の静特性は直線関係ではないため、ダイオードは非線形素子ですよね。

いっぽう、動作点 $${ V_{\rm{D,0}} }$$ の周りでの交流電圧信号（複素振幅 $${ V_{\rm{d}} }$$ ）を入力すると、出力となる交流電流信号の複素振幅 $${ I_{\rm{d}} }$$ は $${ I_{\rm{d}} = (dI/dV) V_{\rm{d}} }$$ となります。この電流と電圧の間の比例係数は動作点周辺での静特性の傾きで与えられ、その値は動作点により異なりますが、いずれにせよ交流信号からみた入出力特性は線形な比例関係にあり、その比例係数は $${ (dI/dV) }$$ として与えられます。

つまりダイオードを交流の目で見たときには、あたかも抵抗値
$${ R_{\rm{d}} = \frac{ k_{\rm{B}} T }{ q I_{\rm{S}} } e^{-q V_{\rm{D,0}} / k_{\rm{B}} T} }$$
をもつ抵抗であるかのように見なせるということです。ただしこの $${ R_{\rm{d}} }$$は動作点 $${ V_{\rm{D,0}} }$$ により値が変わることに留意してください。

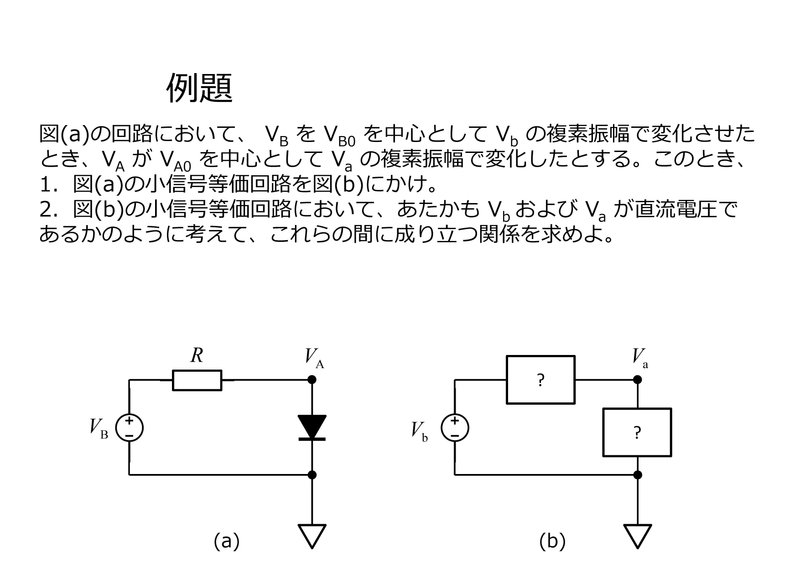
例題その2

以上をふまえて、次の例題に取り組んでください。

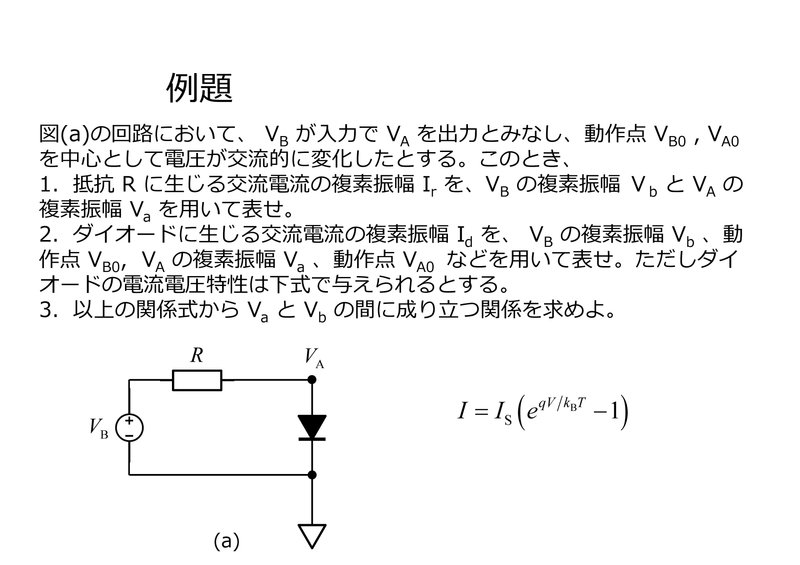
この例題ではまず、回路に含まれる抵抗およびダイオードに対して、交流電流の複素振幅と交流電圧の複素振幅の間に成り立つ関係式を求めます。

問1では抵抗での関係式を求めますが、その解は
$${ I_{\rm{r}} = \frac{V_{\rm{b}} - V_{\rm{a}}}{R}      }$$
となります。

次に問2ではダイオードでの関係式を求めますが、その解は
$${ I_{\rm{d}} = \frac{V_{\rm{a}}}{R_{\rm{d}}}  }$$
と書くことができます。ただし $${ R_{\rm{d}} }$$はダイオードが交流信号の複素振幅に対して示す比例係数を抵抗とみなしたものであり、次式で与えられます:
$${ R_{\rm{d}} = \frac{ k_{\rm{B}} T }{ q I_{\rm{S}} } e^{-q V_{\rm{A,0}} / k_{\rm{B}} T} }$$

問3では、電流が保存されるという条件式 $${ I_{\rm{r}} = I_{\rm{d}} }$$ を上記の関係式に加え、出そろった数式を連立させることで $${ V_{\rm{a}} }$$ と $${ V_{\rm{b}} }$$ の関係式を求めます。その答えは下記のようになり、当然ですが例題その2の解と同じものとなります:
$${ \frac{V_{\rm{a}}}{V_{\rm{b}}} = \left[ 1+\frac{q R I_{\rm{S}}}{k_{\rm{B}}T} e^{q V_{\rm{A, 0}}/k_{\rm{B}}T} \right]^{-1} }$$

小信号等価回路

例題その2を実際に自分で解いて計算過程を眺めると良くわかりますが、交流電圧および交流電流の複素振幅のあいだに成り立つ方程式は、抵抗でもダイオードでも結局はオームの法則のような「抵抗」的な関係式であらわされています。

ではここで頭の中を切り替えて、次のように考えてみてはどうでしょうか？
「回路中の抵抗は、交流電圧と交流電流にとって抵抗だ。あたりまえだな。」
「回路中のダイオードは、交流電圧と交流電流にとってあたかも抵抗のように見なせそうな関係式が成り立っているな。」
「これらの関係式を連立させて解くことで $${ V_{\rm{a}} }$$ と $${ V_{\rm{b}} }$$ の関係を求められるということか。」
「ん？あれ？実はこのプロセスって、交流電圧の複素振幅 $${ V_{\rm{a}} }$$, $${ V_{\rm{b}} }$$ と交流電流の複素振幅 $${ I_{\rm{r}} }$$,  $${ I_{\rm{d}} }$$を、あたかも直流の電圧と電流であるかのように見なして回路解析をするというプロセスと全く同じなんじゃないか？」

はい、その通りです。

実際の回路を、いったん「交流の目で見た回路」に置き換えて、そこからはあたかも交流電圧と交流電流の複素振幅が直流の電圧や電流であるかのように見なして回路解析をすると、正しい解が得られます。
このように最初に与えられた回路を「交流の目」でみて等価な回路に置き換えたものを「小信号等価回路」といいます。

例題その3

それでは最後にこの例題に取り組んでください。

ここではまず、与えられた回路(a)を交流の目で見た小信号等価回路(b)に書き換えます。もうすでにおわかりのように、図中の「 ？ 」に入るのはいずれも抵抗ですね。そして問2では、この小信号等価回路をあたかも直流の電気回路を解くような流儀で解いてください。すると、$${ V_{\rm{a}} }$$ と $${ V_{\rm{b}} }$$ の間の関係式は次のように計算することができ、予想通りの答えを得ることができます:
$${ \frac{V_{\rm{a}}}{V_{\rm{b}}} = \frac{R_{\rm{d}}}{R+R_{\rm{d}}} =  \frac{1}{1+R/R_{\rm{d}}} = \left[ 1+\frac{q R I_{\rm{S}}}{k_{\rm{B}}T} e^{q V_{\rm{A, 0}}/k_{\rm{B}}T} \right]^{-1} }$$

この解法の素敵なところは、いったん正しい小信号等価回路に置き換えることができれば、あとは簡単な直流電気回路を解く問題に帰着されることです。みなさんにとって直流電気回路は、既にたくさん解いてきた馴染み深いもので経験も知識も直感も磨かれているので、それをここでの交流解析でも活用することができます。これは便利ですね。

まとめ

今回は抵抗とダイオードの直列接続という簡単な例で解説をしましたが、実際に電子回路の解析をするときにはもっとたくさんの素子が含まれます。特にトランジスターなどの素子が含まれるときの小信号等価回路は抵抗だけで表されるのではありませんし、キャパシタやインダクタが含まれることで複素数で表された抵抗である「インピーダンス」が登場するため、より複雑になります。こんな実践的な回路では、まず小信号等価回路を書き、それを直流ライクに解く、というプロセスでなければ到底計算できないような場面ばかりとなるため、この考え方はとても重要で不可欠なツールとなります。