みてわかる電子回路「小信号等価回路の数式」

小信号等価回路の世界では、電圧や電流の複素振幅があたかも直流の電圧や電流であるかのように見なして問題を解くことで、複素振幅のあいだの関係を容易に求めることができるのでした。ここではそれを数学的にもう少しだけ厳密にとらえてみましょう。
(ご利用にあたり免責事項をご一読ください)

抵抗の場合

まず抵抗の両端で交流電圧 $${ v_a(t) }$$ および $${ v_b(t) }$$ が生じ、抵抗を通して交流電流 $${ i_r(t) }$$ が生じているとします。ここで電圧と電流の間にはオームの法則が成り立ち、下図の数式のような関係が成り立ちます。この関係式に下図中央の数式を代入して整理すると、複素振幅 $${ V_a }$$, $${ V_b }$$, $${ I_r }$$ の間には下図右下の四角で囲まれた関係式が成り立つことがわかります。

つまり複素振幅 $${ V_a }$$, $${ V_b }$$, $${ I_r }$$ の間には、直流電圧や直流電流の間に成立していたようなオームの法則が成立します。

ダイオードの場合

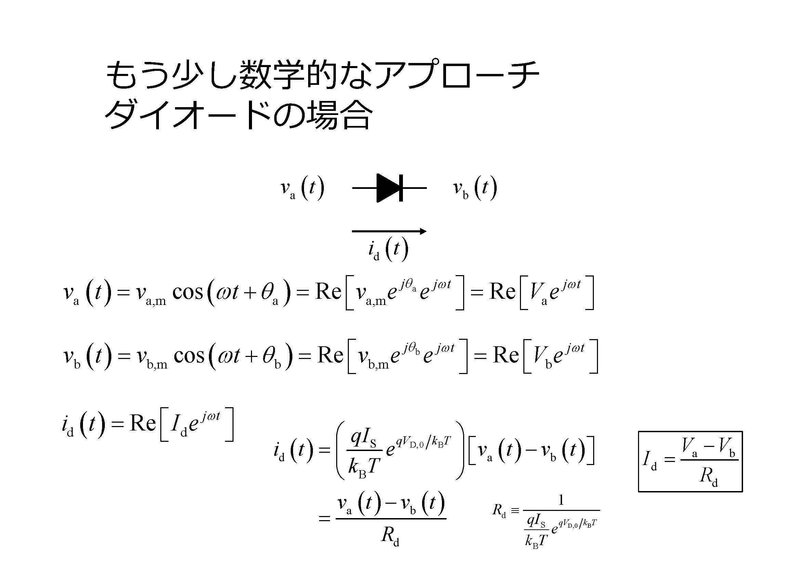
次にダイオードの両端で交流電圧 $${ v_a(t) }$$ および $${ v_b(t) }$$ が生じ、ダイオードを通して交流電流 $${ i_d(t) }$$ が生じているとしましょう。ここで電圧と電流の間には、動作点周辺での電流電圧特性の傾きを用いて、図下部の数式のような関係が成り立ちます。この関係式に図中央の数式を代入して整理すると、複素振幅 $${ V_a }$$, $${ V_b }$$, $${ I_d }$$ の間には図右下の四角で囲まれた関係式が成り立ち、オームの法則のような比例関係となります。ただしここでの抵抗に相当するものは、動作点によって変化するので注意が必要です。

キャパシタの場合

次にキャパシタの両端で交流電圧 $${ v_a(t) }$$ および $${ v_b(t) }$$ が生じ、キャパシタを通して交流電流 $${ i_c(t) }$$ が生じているとしましょう。ここでも下図中の計算により、複素振幅 $${ V_a }$$, $${ V_b }$$, $${ I_c }$$ の間には図右下の四角で囲まれた関係式が成り立ち、オームの法則のような比例関係となります。ただしここでの抵抗と等価な量(インピーダンス)は、$${ 1/(j \omega C) }$$ という複素数になります。

インダクタの場合

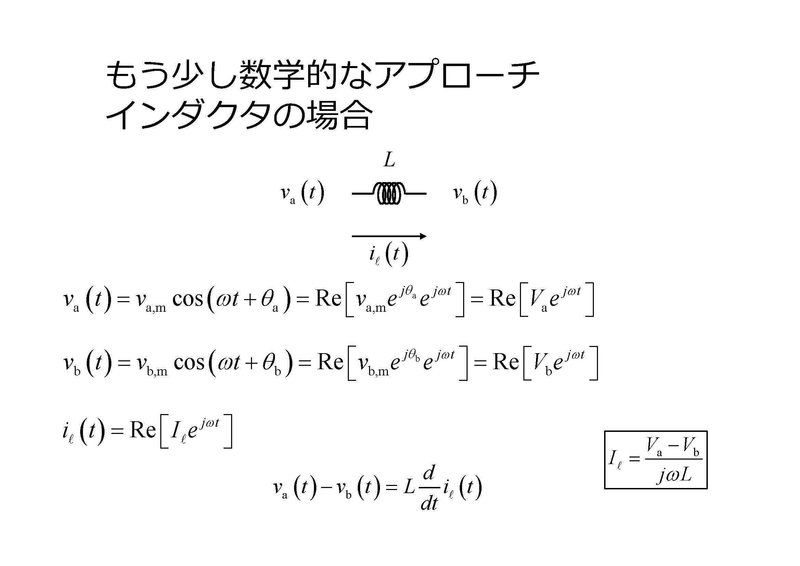
最後にインダクタの両端で交流電圧 $${ v_a(t) }$$ および $${ v_b(t) }$$ が生じ、インダクタを通して交流電流 $${ i_l(t) }$$ が生じている場合もほとんど同様の計算を行うことができます。結果的には、複素振幅 $${ V_a }$$, $${ V_b }$$, $${ I_l }$$ の間にはオームの法則のような比例関係が成立し、ここでの抵抗と等価な量(インピーダンス)は、$${ j \omega L }$$ という複素数です。

以上をまとめると

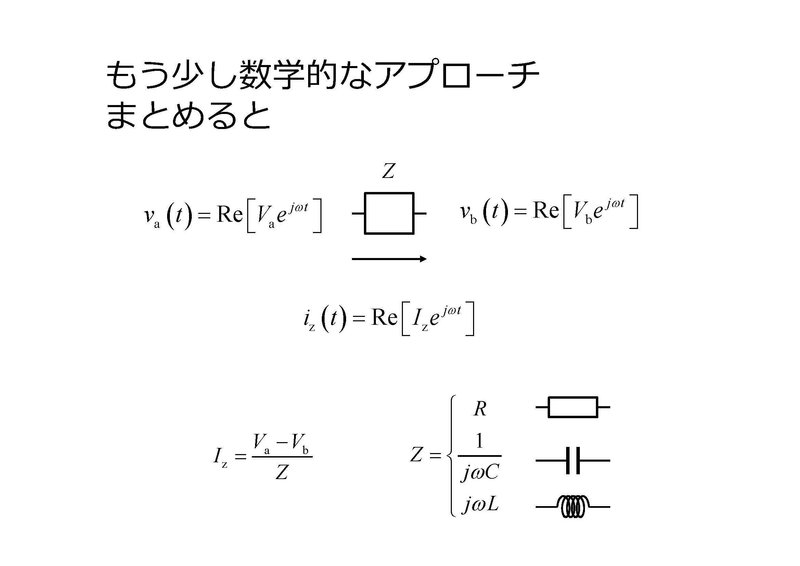
結局のところ、ある素子の両端に生じた交流電圧とそこに生じる交流電流の関係は、インピーダンス(ダイオードの場合は等価な抵抗)に置き換えることで全てがオームの法則と同じ単純な形で表されます。複数の素子が組み合わさった回路での関係を考えるときには、これらの「直流ライク」な関係式を組み合わせて問題を解いていくことになります。

この計算過程を別の視点で見ると、電圧や電流の複素振幅をあたかも直流であるかのように見なして、素子のインピーダンスが組み合わさった回路網での直流的な電気回路の問題を解いているとみることもできます。
このようにして、小信号等価回路に置き換えたあとは簡単な直流電気回路的な解析を行うことで、交流信号の複素振幅の間に成り立つ関係式を正しく計算することができるのですね。

ちなみにトランジスタが加わると

くわしくは別の記事で解説しますが、トランジスタのような素子を交流の目で見ると、抵抗や電流源といった複数の素子が組み合わさった一つの電気回路ブロックとしてみなすことができます。そして小信号等価回路に書き換えた後は、今まで通り直流ライクに回路解析を行うことで、交流の複素振幅の間の関係式を求めることができます。