みてわかる電子回路「二素子が直列接続された回路の動作」

ここでは、電子回路を習得するうえで大切な思考ツールについて説明します。ここで述べる思考ツールを習得すれば、電子回路の定性的な挙動（ざっくりとした動き）を視覚的に図を用いて簡単に把握することができます。目に見えない電流や電圧といったものの動きを、図を用いて視覚的にビジュアル化することで、電子回路の理解が桁違いに向上するので、ぜひ習得してご活用ください。
(ご利用にあたり免責事項をご一読ください)

直列接続された二つの抵抗

二つの抵抗が直列接続されており、全体に直流電圧 $${V_{\rm{D}}}$$ [V] が印加されています。全体に直流電流 $${I_{\rm{D}}}$$ [A] が生じており、二つの抵抗の間にある端子の電圧を $${V_{\rm{A}}}$$ [V] とします。簡単な計算により、$${I_{\rm{D}}}$$ と $${V_{\rm{A}}}$$ が下図中の式のように求まります。このような方法をとれば計算できる、ということを高校のときに教わっているので、その通りに計算すれば答えを得ることは簡単ですよね。でも、これだけでは何がどうなっているかが「見え」てきません。

電流と電圧を視覚化する

ここで起こっていることを「見えてくる」ようにするために図を活用してみましょう。まずは、抵抗 $${R_{\rm{1}}}$$ をいったん取り除いて、抵抗 $${R_{\rm{2}}}$$ だけに着目します。この上端の電圧 $${V_{\rm{A}}}$$ は、本来は $${V_{\rm{D}}}$$ が与えられれば一意にきまる定数のはずです。ですがここであえて、仮想的にこの電圧が自由に変化する変数である、と考えて、それを $${V}$$ としましょう。このとき、抵抗 $${R_{\rm{2}}}$$ に生じる電流 $${I_{\rm{2}}}$$ は $${V}$$ の関数とみなすことができます。そしてこの電流と電圧の関係を図で視覚化すると、スライド中の右図のようになります。

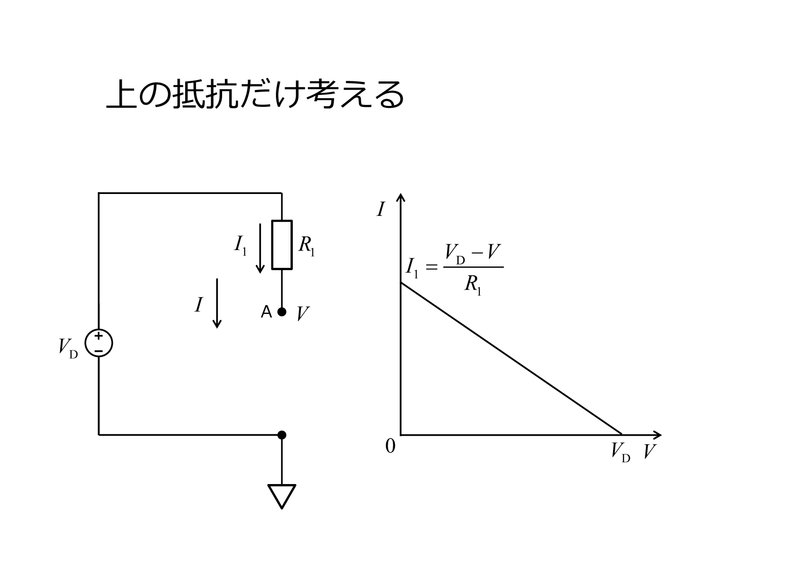
次は、抵抗 $${R_{\rm{2}}}$$ を取り除いて、抵抗 $${R_{\rm{1}}}$$ だけに着目しましょう。 $${R_{\rm{1}}}$$ の下の電圧は、再び自由に変化できるものと仮想的に見なして、変数 $${V}$$ で表します。このときに抵抗 $${R_{\rm{1}}}$$ に生じる電流 $${I_{\rm{1}}}$$ を $${V}$$ の関数とみなして図示すると、下図のようになるでしょう。

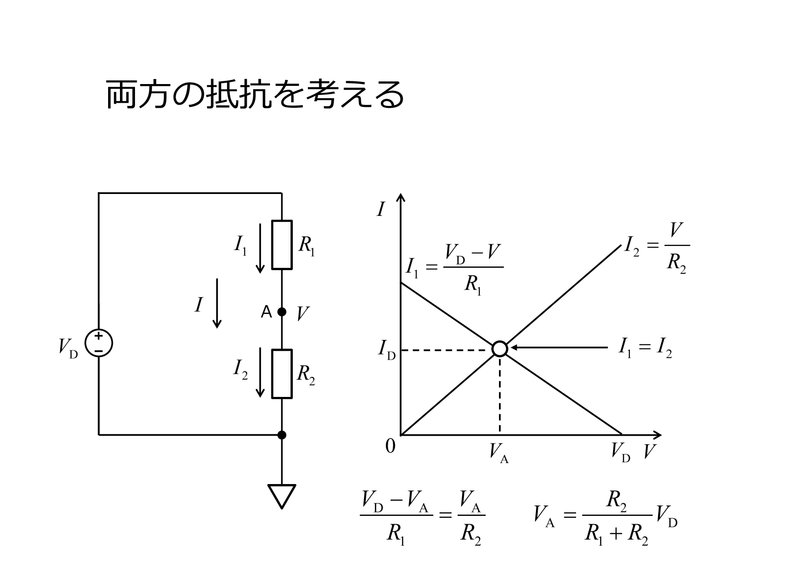
実際には抵抗 $${R_{\rm{1}}}$$ と $${R_{\rm{2}}}$$ はつながっていて、お互いに関係しあっているので、$${I_{\rm{1}}}$$ の線と$${I_{\rm{2}}}$$ の線を同じ図に同時に描きます。ここで、$${R_{\rm{1}}}$$ に生じた電流 $${I_{\rm{1}}}$$ はどこにも逃げることなくそのまま $${I_{\rm{2}}}$$ になることを考えると、この回路で「実際に実現する」状態は、これらが等しい状態に限られるはずですよね。図のなかでは、二つの線が交わる交点によって与えられる状態に他なりません。この交点から、この回路で実際に実現する $${I_{\rm{D}}}$$ と $${V_{\rm{A}}}$$ が求まります。具体的に計算したいときは、$${I_{\rm{1}} = I_{\rm{2}}}$$ という関係式から $${V_{\rm{A}}}$$ に関する方程式を導出して、それを解けば答えを得ることができます。

直列接続された任意の二つの素子

以上の考え方は、抵抗に限らず、任意の素子について成り立ちます。ダイオードでも、トランジスターでも、複数の素子の組み合わせによる二つの回路ブロックが直列接続されている場合でも同様です。この際、電流電圧特性は必ずしも抵抗のような直線となるとは限りません。でもやはり二つの線の交点は必ず存在し、それが実際に実現する $${I_{\rm{D}}}$$ と $${V_{\rm{A}}}$$ を知らせてくれるはずです。その時の $${V_{\rm{A}}}$$ は、スライド中の式のように $${I_{\rm{1}} = I_{\rm{2}}}$$ という条件から導き出される方程式を解くことで得られます。