みてわかる電子回路「増幅回路が扱う信号」

ここからは信号を増幅する回路についての話が始まります。それに先立ち、そもそもこの回路が扱う信号とは？というところについて考えておきましょう。
(ご利用にあたり免責事項をご一読ください)

まずは記号の定義から

ここからの説明では、正弦波的に変化する電圧や電流を信号として取り扱います。その中に含まれる様々な成分の定義を明確にするために、下図中のように変数の「書き方」を定めておきましょう。

まず、最も一般的な変数の時間変化は、小文字で書かれた変数名に大文字で書かれた添え字をつけることとします。そのなかの時間的に変化しない直流成分は、大文字で書かれた変数名に大文字で書かれた添え字をつけます。一方、時間的に変化する交流成分は、小文字で書かれた変数名に小文字で書かれた添え字をつけます。そしてその振幅には小文字で書かれた変数名に小文字で書かれた添え字「m」を付記することとしましょう。以上のルールに従って変数を書くと、これらの間には下図一番下の数式のような関係が成り立ちます。

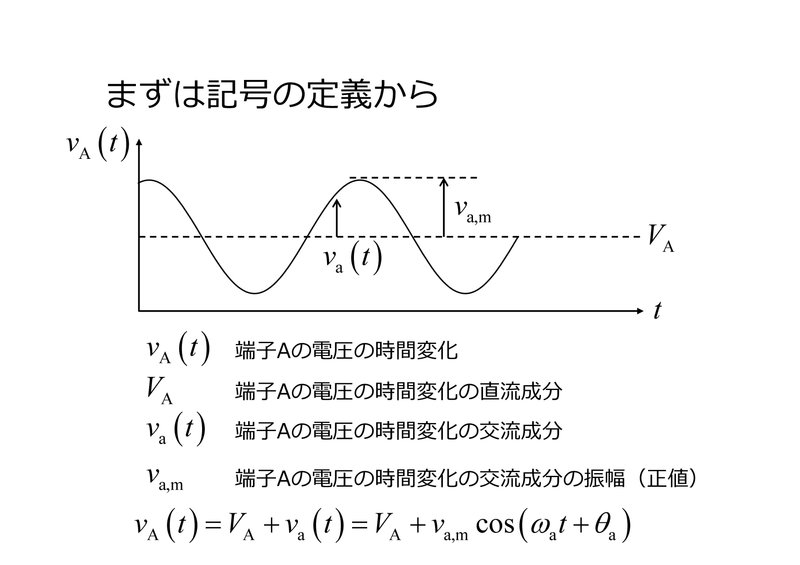
ここからの説明では、この中でも特に交流成分が重要な役割を果たします。ここでは三角関数を用いて時間依存性や位相シフトが表現されていますが、数学的な計算や回路解析を行うときは、これを複素数によって表すほうがずっと便利で分かりやすく、計算もずっと楽になります。

具体的には、下図中の数式のように三角関数を複素数の表記に変形します。ちなみにRe[…]は複素数…の実数部分を表します。
このなかで、複素数で表された部分（Re[...]の…の部分）の時間に依存しない項( $${v_{\rm{a,m}} e^{j\theta}}$$ )を、大文字で書かれた変数名に小文字で書かれた添え字をつけて書く( $${V_{\rm{a}}}$$ )こととします。この変数が今後の話のなかで最も重要な役割を果たします。

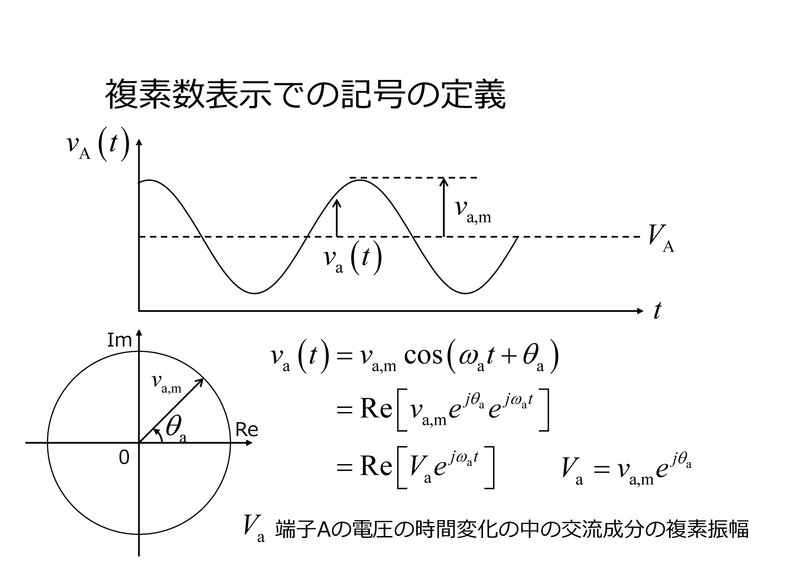
この変数は、交流成分の振幅（正の実数）を「大きさ」にもち、交流成分の位相成分を「位相」にもつ複素数です。この講義では、これを「複素振幅」と呼ぶこととしましょう（他にもフェーザーなどとよばれる場合もあります）。この複素振幅は、交流波の振幅の大きさに関する情報と位相に関する情報を併せ持つ変数であり、交流信号の強度や位相が変化する回路の解析や計算において主要な役割を果たします。

ではここから取り扱う「信号」とは？

この講義のなかでの「信号」とは、「変化のないところに生じる変化」を意味します。この変化の波形が信号としての情報を持ち、送信され、伝搬し、受信されます。例えば皆さんの耳に聞こえる声。これは変化のない空気に喉が振動という変化の波を発生させ、それが空間の中を伝搬し、耳によって受信されていますよね。同じようにして、電子回路では変化のない端子電圧が微小に変動し、それが回路網を伝わっていきます。

ここで信号という「変化」が生じるには、まずそれを伝達するための「変化のないところ」が必要となります。たとえば声の場合は、「変化のないところ」＝「じっとしている空気」、「変化」＝「空気の圧縮と膨張」となりますし、電子回路の場合は、「変化のないところ」＝「直流電圧」、「変化」＝「電圧の変動」となります。

複雑な信号を単純な信号で表す

でもちょっと待ってください。実世界での信号は、ここまで見てきたような簡単な正弦波とは異なり、とても複雑に変化しますよね。ここで横軸を時間として信号の変化を表すと、様々な複雑な形状をしているでしょう。

そのような信号の解析を行う上で便利なツールの一つとして、フーリエ変換があります。これを用いると、任意の波形を持つ信号は、様々な周波数の正弦波の重ね合わせで表すことができます。ここで、各周波数の正弦波がどの程度の「濃さ」で混ぜ合わされるかを表すものを「スペクトル」といい、横軸を時間とした波形に対して一意的に定まります。

このように考えると、どんなに複雑な波であっても、結局はいろいろな周波数の正弦波の混ぜ合わせとなります。回路の解析を行うときは、この中のある周波数の正弦波に対する解析を行うだけで用が済むので、とても便利な考え方です。
以上のような事情から、ここから増幅回路について学習するうえで取り扱う信号は正弦波であるとみなしても差し支えありません。