現代ポートフォリオ理論：Modern Portfolio TheoryをPythonで実践してみる。

2024年3月6日 19:54

現代ポートフォリオ理論：Modern Portfolio Theoryとは？

現代ポートフォリオ理論：Modern Portfolio Theory (略：MPT) は1952年にハリー・マーコウィッツによって発表された金融資産への投資比率（ポートフォリオ）を決定する理論。

Pythonによる実装

環境はGoogle Corabです。

ライブラリの読み込み

import datetime as dt
import pandas as pd
import pandas_datareader.data as web
import yfinance as yf

yf.pdr_override()

株式銘柄の選択とヒストリカルデータの取得

stocks = [7203, 6758, 6861, 9432, 8306, 4568, 4502, 8316, 6501, 7974]

上記の銘柄はTOPIX構成銘柄から適当に選択しており、特に理由はありません。株式銘柄のヒストリカルデータが必要になるため、Yahoo Financeからデータを取得します。データの取得にはpandas_datareaderライブラリを利用します。

prices = []
for stock in stocks:
    try:
        closes = web.DataReader(str(stock) + ".T", start='2023-01-01', end='2023-12-31')["Adj Close"]
        closes_df = pd.DataFrame(closes)
        closes_df.columns = [stock]
        prices.append(closes_df)
    except:
        pass
    prices_df = pd.concat(prices, axis=1)

prices_df.sort_index(inplace=True)

ポートフォリオの期待リターンと共分散を計算

ポートフォリオの最適化に必要な計算を行うために、PyPortfolioOptというライブラリをインストールします。

PyPortfolioOptのインストールを行います。

!pip install PyPortfolioOpt

期待リターンと共分散を計算するために必要なrisk_models, expected_returnsをインポートします。

from pypfopt import risk_models, expected_returns

期待リターンを計算します。

mu = expected_returns.mean_historical_return(prices_df)
mu

期待リターンをプロットしてみます。

import plotly.express as px

fig = px.bar(x=[str(x) for x in mu.index], y=mu.values, title="期待リターン")
fig.show()

次に共分散を計算します。

S = risk_models.sample_cov(prices_df)
S

共分散行列をヒートマップにして可視化してみます。

import seaborn as sb

fig = plt.figure()
sb.heatmap(S, annot=True)
plt.show(fig)

シャープレシオの最大化

シャープレシオの最大化はmax_sharpe()で行います。
上記で計算した期待リターンと共分散を用いて計算します。

ef = EfficientFrontier(mu, S)
weights = ef.max_sharpe()
weights

投資比率を端数処理するためのメソッドも用意されています。
clean_weights()はデフォルトで小数点以下5桁で四捨五入します。

cleaned_weights = ef.clean_weights()
cleaned_weights

ポートフォリオのパフォーマンスを見てみる

最適化された投資比率でポートフォリオのパフォーマンスを知りたい場合は、portfolio_performance()を使って確認出来ます。

ef.portfolio_performance(verbose=True)

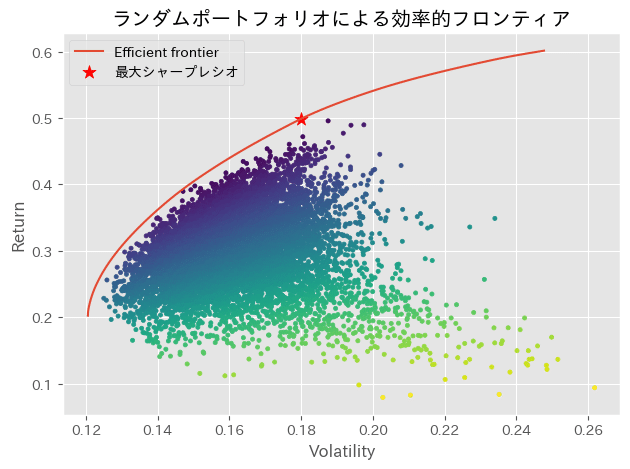
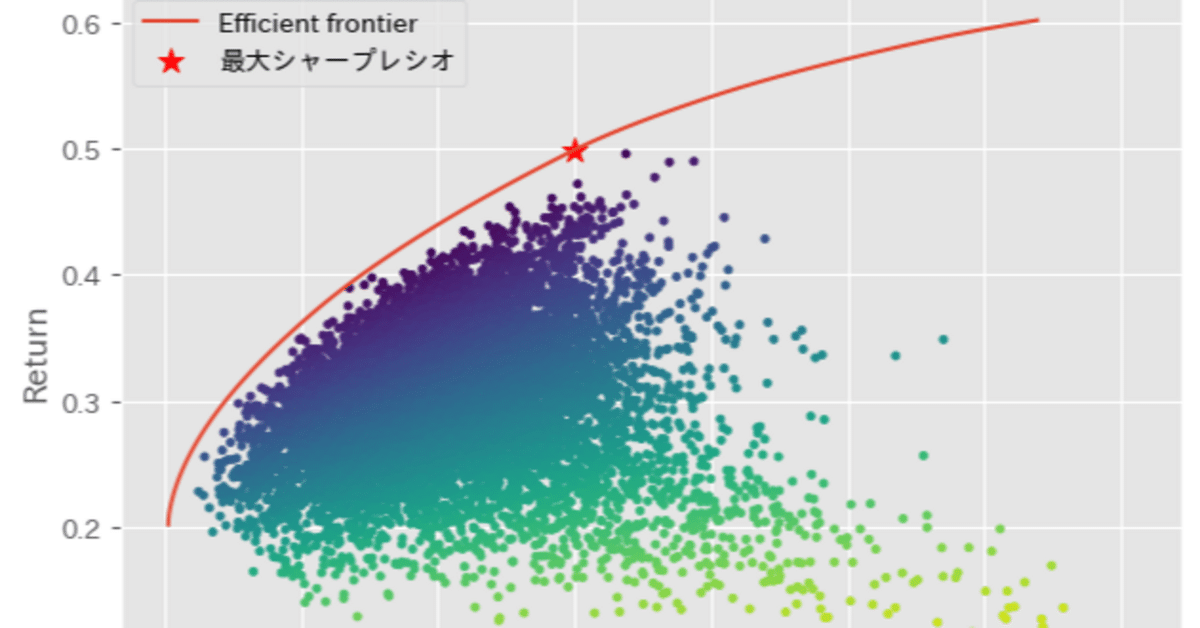
効率的フロンティアの可視化

最後にPyPortfolioOptのドキュメントにある効率的フロンティア可視化のコードでプロットを行ってみます。

ef = EfficientFrontier(mu, S)

fig, ax = plt.subplots()
ef_max_sharpe = ef.deepcopy()
plotting.plot_efficient_frontier(ef, ax=ax, show_assets=False)

# 接点ポートフォリオを見つける
ef_max_sharpe.max_sharpe()
ret_tangent, std_tangent, _ = ef_max_sharpe.portfolio_performance()
ax.scatter(std_tangent, ret_tangent, marker="*", s=100, c="r", label="最大シャープレシオ")

# ランダムなポートフォリオを生成
n_samples = 10000
w = np.random.dirichlet(np.ones(ef.n_assets), n_samples)
rets = w.dot(ef.expected_returns)
stds = np.sqrt(np.diag(w @ ef.cov_matrix @ w.T))
sharpes = rets / stds
ax.scatter(stds, rets, marker=".", c=sharpes, cmap="viridis_r")

# 出力
ax.set_title("ランダムポートフォリオによる効率的フロンティア")
ax.legend()
plt.tight_layout()
plt.show()