8月東大本レ大問5をゆるり解説する枠

すぐ解説が始まるので、暇な人はここで1度立ち止まって考えてみるのもいいと思います。

こんちは。うるとらまりんです。本人です一応真面目なこともできます。
今回は6月東大本レの(僕が解けずに0点だった)大問5をテキトーに解説しようかなって思います。

まず(1)ですが、絶対値の制約より考えられることは2つあります。
①共役複素数と絡めて式を変形する
②極形式として表して式を変形する

とりあえずこのふたつを頭の中でキープしておきましょう。
さて、示すべきことは「α、β、γの『少なくともひとつは』1であること」なので、背理法か(α-1)(β-1)(γ-1)=0を示すかのどちらかを優先的に考えたいです。今回は対称性が高く、式変形が結構刺さりそうだなあと言うとんでもなく主観的で根拠の無い印象から後者を選択します。(暇な人は前者も考えてみてください。僕は思いつきませんでした。というより背理法だとしても結局(α-1)(β-1)(γ-1)≠0という仮定が議論の出発点なので余り変わらなさそう。)

これを踏まえると、示すべき形から、α、β、γはそのままの形で扱ったほうがいいと分かるので、①を選択しましょう。

さて、ここまで何となく解法を整理してきましたが、このままでは式が足りず、証明ができません。そこで、

α+β+γ=1の両辺を共役複素数にする

という操作をします。そうすると、絶対値の条件から共役複素数は削除できて、突破口が開けますね。
解答は以下です。

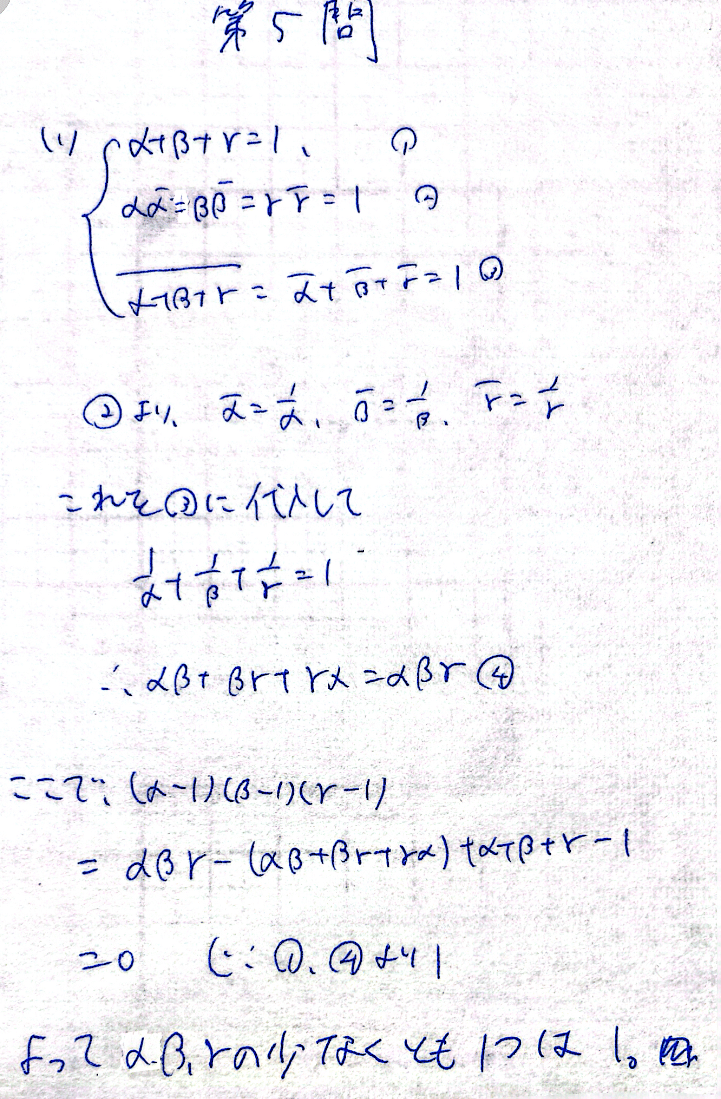
(ちなみに②の極形式を扱った解法も無くはないですが、とんでもなくゴミクソ面倒なので触れません。あと実はこの2つ以外にも、絶対値の制約を使った解法が2つあるので暇な人は考えてみてください。ひとつは文字消去、もうひとつは解と係数の関係を使います。)

(2)です。まず偏角の条件から直ぐにα=1と分かります。あとはβ、γを面積の条件から求めるだけですね。

β、γをどう表すかについてですが、座標における面積は数字のまま計算した方が基本早いので今回は極形式ではなくu+viと文字で置いて計算します。
また、基本的に文字の制約は強ければ強いほど良いので、今回の答案では最初にvの範囲を絞っています。

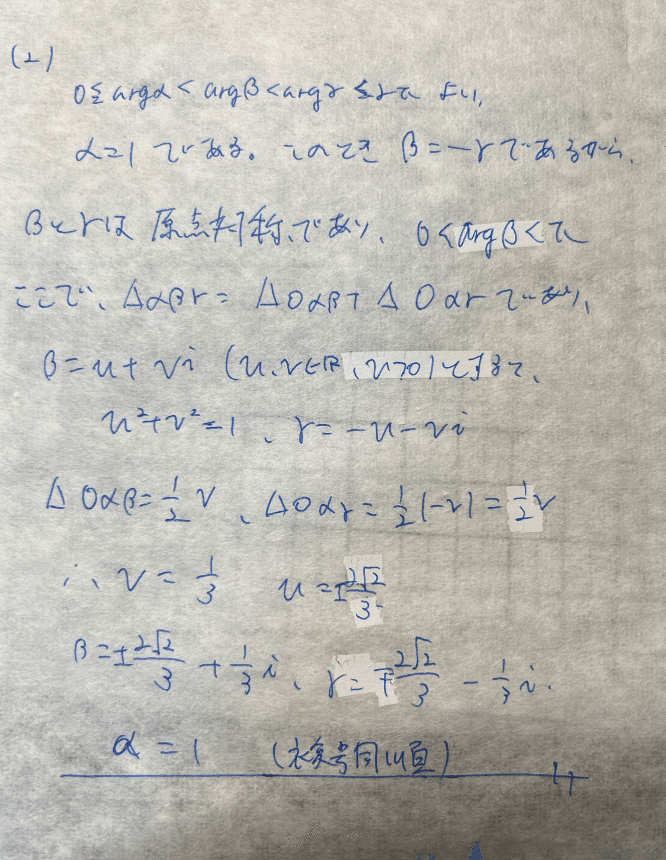
以下解答です。

あとがき

分かりにくい割に長い解説と汚い字でごめんなさい。
今回の問題、自分も見た時は手も足も出なかったので、ある意味自戒というか、復習の意味も込めて解答を書いてみました。少しでも役に立てば幸いです。
(今回は最初から最後まで全部本当のこと書いてます)