適応型移動平均について(続き)
↑の記事の続きです。MT5で新規に搭載された残り二つの適応型移動平均を紹介します。
Fractal Adaptive Moving Average(フラクタル適応型移動平均)
フラクタル適応型移動平均(FRAMA)も、基本的な考え方はEMAと同じです。
EMA[i]=a[i]×Close[i] + (1-a[i])×EMA[i-1]
違いは平滑化パラメータa[i]の計算方法なのですが、FRAMAの特徴は「フラクタル次元」という考え方を利用する点にあります。
詳しいことは省略しますが、直線状に変化するトレンド相場の場合、フラクタル次元を1、同じ動きを繰り返すレンジ相場の場合、フラクタル次元を2と考える、ということです。
つまり、フラクタル次元をD[i]とすると、D[i]が1のときにトレンド相場なので、EMAの平滑化パラメータa[i]を1に、D[i]が2のときにレンジ相場なので、a[i]を0になるように置き換えたいわけです。
FRAMAでは、D[i]からa[i]への変換に次のような式を使います。
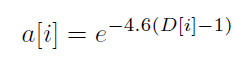
この式だけではよくわかりませんが、グラフにすると下のようになります。
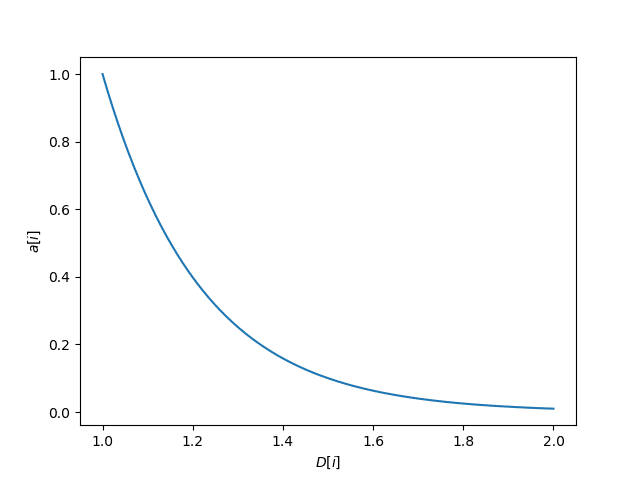
これは、D[i]が1のときにa[i]が1になるように変換しますが、D[i]が2のときは、a[i]が0ではなく、0.01になるように変換しています。平滑化パラメータが0.01というのは、移動平均の期間でいうと199です。つまり、長期移動平均の期間としてよく利用される200以上には平滑化しないようにしているのです。
さて、次にフラクタル次元D[i]の算出方法ですが、次のような式で算出します。
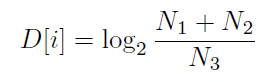
ここで、N1、N2、N3はそれぞれ以下のように求めます。
N1:直近N期間の最高値と最安値の差/N
N2:N+1から2Nまでの期間の最高値と最安値の差/N
N3:直近2N期間の最高値と最安値の差/2N
ここで、NがFRAMAのパラメータであり、トレンドかレンジの判別に利用する期間となります。
D[i]の数式の意味は、(N1+N2)/N3が2のときにD[i]が1に、(N1+N2)/N3が4のときにD[i]が2になるというものです。トレンド相場とレンジ相場でそれそれの値がどうなるか見てみましょう。
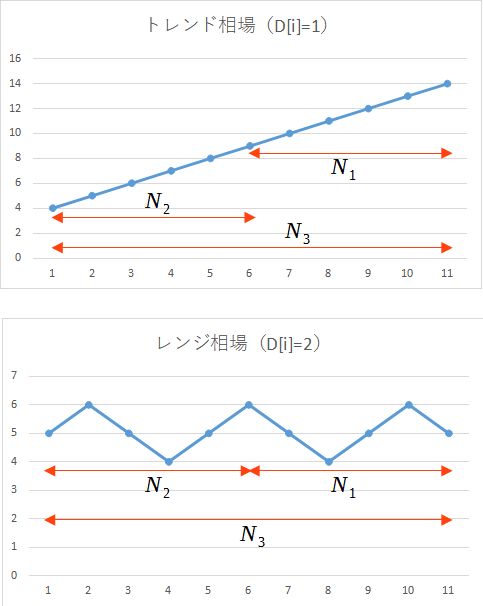
いま、N=5とします。上のグラフで矢印の範囲は、それぞれN1、N2、N3を求める範囲を表しています。
トレンド相場の場合、直近N本の最高値と最安値の差は5なので、N1=5/5=1です。同様にその前のN本の最高値と最安値の差も5なので、N2=5/5=1となります。そして、直近2N本の最高値と最安値の差が10なので、N3=10/(2*5)=1となります。その結果、(N1+N2)/N3=(1+1)/1=2より、D[i]=1となるわけです。
レンジ相場の場合、直近N本の最高値と最安値の差、およびその前のN本の最高値と最安値の差は2です。したがって、N1=N2=2/5=0.4となります。また、直近2N本の最高値と最安値の差も2なので、N3=2/(2*5)=0.2となります。その結果、(N1+N2)/N3=(0.4+0.4)/0.2=4より、D[i]=2となるわけです。
以上より、トレンド相場に近ければD[i]が1に近づき、a[i]が1に近づくため、直近の価格の重みが大きくなり、価格変動に素早く追従するようになります。逆にレンジ相場では、D[i]が2に近づき、a[i]が0.01に近づくことで、長期的な移動平均となり、動きが緩やかになるというわけです。
チャートに挿入して確認してみましょう。FRAMAのパラメータがN=14の場合です。
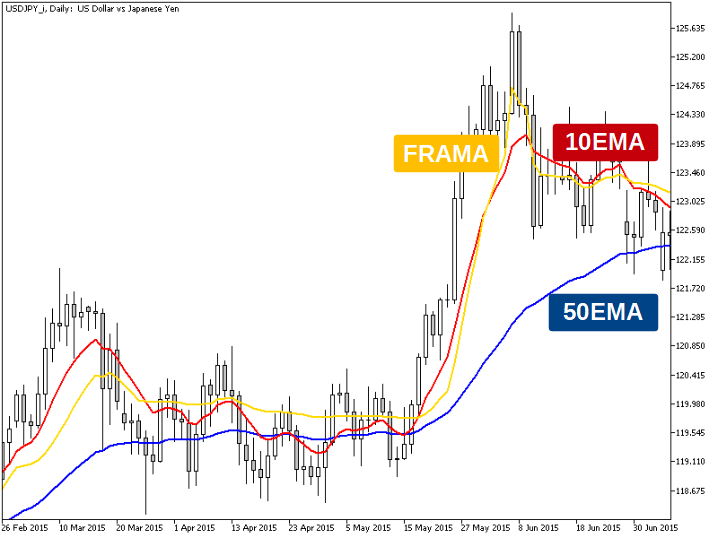
前回のAMAとは若干動き方が違いますが、トレンド相場では短期移動平均、レンジ相場では長期移動平均に近い形になっていることがわかります。
Variable Index Dynamic Average(可変インデックス動的平均)
もう一つ、Variable Index Dynamic Average(VIDYA)を紹介します。ほかの適応型移動平均と同じくEMAの計算式を使います。
EMA[i]=a[i]×Close[i] + (1-a[i])×EMA[i-1]
今回は、a[i]の基準値として、通常のEMAの平滑化パラメータを使います。つまり、期間EMAperiodに対応する平滑化パラメータはa[i]=2/(EMAperiod+1)なので、これを基準値とします。
そして、この基準値に対してChande モメンタムオシレータ(CMO)と呼ばれる指標の絶対値を掛けて変動パラメータとします。a[i]は次式のように書けます。
a[i] = Abs(CMO[i])×2/(EMAperiod+1)
ここで、CMO[i]は次のように計算されます。
CMO[i]=(UpSum[i]-DnSum[i])/(UpSum[i]+DnSum[i])
UpSum[i]:1本前からの変化がプラスとなるものの合計
DnSum[i]:1本前からの変化がマイナスとなるものの合計
理想的なトレンド相場では、UpSum[i]だけ、あるいはDnSum[i]だけになるので、CMO[i]の絶対値は1に近づきます。一方、レンジ相場では、UpSum[i]とDnSum[i]が拮抗するため、CMO[i]は0に近づきます。
つまりVIDYAでは、基準となる平滑化パラメータに、0から1の範囲で変化するパラメータを掛けることで、平滑化パラメータを変動させているのです。
VIDYAでは、基準の平滑化パラメータの元になるEMAの期間(EMAperiod)と、CMO[i]を算出する期間(CMOperiod)がパラメータとなります。
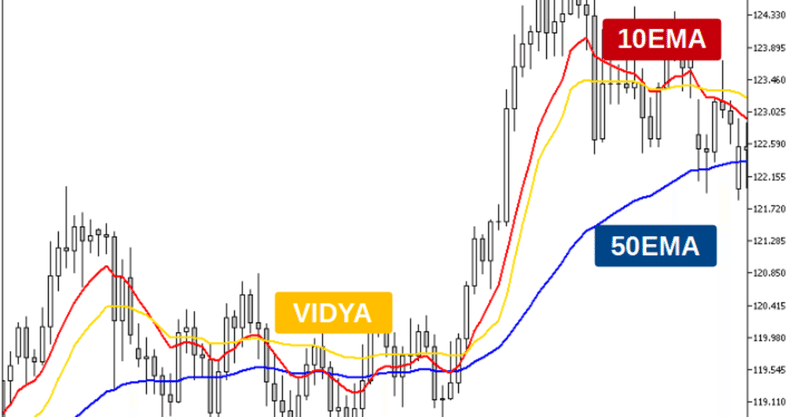
EMAperiod=CMOperiod=10の場合のVIDYAをチャートに表示すると以下のようになります。
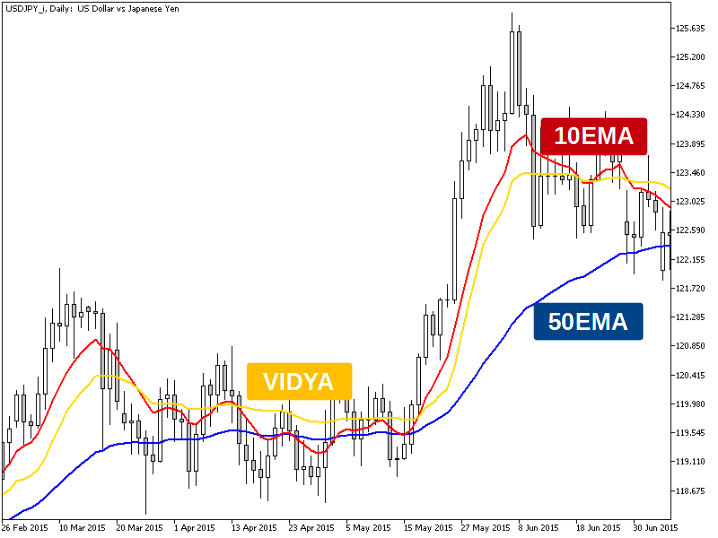
これも同じようにトレンド相場では短期移動平均、レンジ相場では長期移動平均に近い形になっています。
以上3つの適応型移動平均を紹介しました。元の説明は以下のサイトにありますので、ご参考にしてください。
この記事が気に入ったらサポートをしてみませんか?
