適応型移動平均について

MT4にはなくてMT5から新規に組み込まれたテクニカル指標に「適応型移動平均」があります。

適応型移動平均にはいくつかバリエーションがあり、MT5では以下の３種類の適応型移動平均が使えるようになっています。

・Adaptive Moving Average（適応型移動平均）
・Fractal Adaptive Moving Average（フラクタル適応型移動平均）
・Variable Index Dynamic Average（可変インデックス動的平均）

適応型移動平均とは？

通常移動平均と言えば、平均する期間を決めて、その期間の価格に適当な重みをつけて平均化します。

適応型移動平均とは、簡単に言うと、相場の途中で平均する期間を変える機能をもった移動平均です。例えば、ある期間では１０本の平均を取るけど、別の期間では５０本の平均を取るなどです。

期間の変え方は自由ですが、一般に移動平均はトレンドを判別する目的で使われます。トレンドがあるときはトレンドに沿って動き、トレンドがないときはあまり変化しない方が望ましいと言えます。

以下のチャートは従来の移動平均の動きを表したものです。

赤いラインが１０本のEMA（指数平滑化移動平均、詳しくは後ほど説明します）、青いラインが５０本のEMAです。

トレンド相場ではトレンドに素早く反応してほしいので、10EMAの方が好ましいと言えます。しかし、レンジ相場では下手に動かないでほしいので、50EMAの方がいいわけです。

適応型移動平均は、これらのいいところを一つの移動平均でできないか、ということで考案されたものと言えます。

適応型移動平均の仕組み

適応型移動平均の基本は、指数平滑化移動平均（EMA）です。まずはEMAについて説明します。

EMAは以下のような式で計算されます。

EMA[i]=a×Close[i] + (1-a)×EMA[i-1]

ここで、Close[i]が現在の終値、EMA[i]が現在のEMA、EMA[i-1]が１本前のEMAを表します。またaは０から１までの実数値を取るパラメータです。aと1-aを足すと1になることから、Close[i]とEMA[i-1]の平均を取った式となっています。期間のパラメータと区別するために、aのことを平滑化パラメータと呼ぶことにします。

ところでMT4やMT5でEMAを表示させる場合、パラメータとして期間を指定します。上のチャートでも１０本のEMAや５０本のEMAという言い方をしました。

ただし、EMAの期間は、実際に平均の計算に利用するデータの期間ではありません。通常EMAの期間Nは、a=2/(N+1)という式で平滑化パラメータaに置き換えて計算を行います。

どうしてa=2/(N+1)かというと、直近の重みを線形加重移動平均（LWMA）に合わせているからです。

LWMAは直近の重みが一番大きく、過去にさかのぼるにつれ、重みを直線状に小さくしていきます。例えば、N=9の場合、１から9まで足した値が45なので、重みは9/45、8/45、・・・2/45、1/45となります。

EMAの場合、直近の重みはaになりますが、a=2/(N+1)とすると、N=9の場合、a=2/(9+1)=0.2となり、LWMAの直近の重み9/45=0.2と一致します。

EMAとLWMAの重みの違いは下図のようになります。

LWMAの場合、N=9なら9個のデータしか使いませんが、EMAの場合、Nに関係なく、かなり過去のデータまで使うところが異なります。

単純移動平均SMAやLWMAでは、パラメータが期間Nで、整数の範囲でしか値を変えられません。一方、EMAの場合、平滑化パラメータaが０から１の範囲で変化できる実数パラメータなので、より細かく特性を変えることができるのです。

相場の変化をスムースに移動平均に反映させるには、連続的な値が取れるEMAの平滑化パラメータaが向いているのです。

平滑化パラメータaが変化することを表すためにa[i]と表記すると、一般に適応型移動平均は次のような式で表せます。

EMA[i]=a[i]×Close[i] + (1-a[i])×EMA[i-1]

Adaptive Moving Average（適応型移動平均）

それぞれの適応型移動平均では、EMAのa[i]の計算方法が異なります。

まず、最初のAdaptive Moving Average（AMA）では、平滑化パラメータを変化させる範囲を決めるために、短期EMAと長期EMAを用意します。これらの期間自体AMAのパラメータですが、ここでは仮に、短期EMAを期間２（a=2/3）、長期EMAを期間３０（a=2/31）としておきます。

そして、０から１まで変化するER[i]というパラメータを使って、ER[i]が０のとき長期EMAを採用、ER[i]が１のときに短期EMAを採用するように平滑化パラメータa[i]を計算します。

a[i] = ER[i]×(2/3-2/31) + 2/31

ここでER[i]はトレンド相場かレンジ相場かを判断するための効率比と呼ばれる指標です。以下のように表します。

ER[i] = Signal[i]/Nose[i]
Signal[i]：Abs(Close[i] - Close[i-N])
Noise[i]：Sum(Abs(Close[i]-Close[i-1]), N)

Signal[i]は一定期間前の終値との差の絶対値を表したもので、モメンタムみたいなものです。Noise[i]は１本前の終値との差の絶対値を一定期間分合計したものです。各足における値動き幅の合計と見ることもできます。トレンド相場とレンジ相場の極端な例で、それらの値がどうなるか見てみましょう。

トレンド相場の場合、最初と最後の価格差が１０なのでSignal[i]が１０になります。また各足で１ずつ変化しているので、それを合計すると、Noise[i]も１０になります。結局、ER[i]=10/10=1となります。

一方、レンジ相場の場合、各足での値動きの絶対値は１なので、それを合計すると、Noise[i]は１０となります。ただ、最初と最後で価格は変わらないので、Signal[i]は０です。したがって、ER[i]=0/10=0となります。

このようにER[i]が１に近づけばトレンド相場ということなので、平滑化パラメータを短期EMAに近づけます。逆にER[i]が０に近づけばレンジ相場ということなので、平滑化パラメータを長期EMAに近づけるようにすればよいわけです。

EMAの計算式で以上のようなa[i]を平滑化パラメータとすれば適応型移動平均となります。ただし、MT5にAMAとして組み込まれている指標では、a[i]の代わりにa[i]^2（a[i]の二乗）を平滑化パラメータとしています。短期EMAと長期EMAの効果の差を広げるためだと思われます。

AMA[i]=a[i]^2×Close[i] + (1-a[i]^2)×AMA[i-1]

AMAをチャートに表示させると以下のようになります。トレンド相場では短期EMAに近い動き、レンジ相場では長期EMAに近い動きになっていることがわかります。

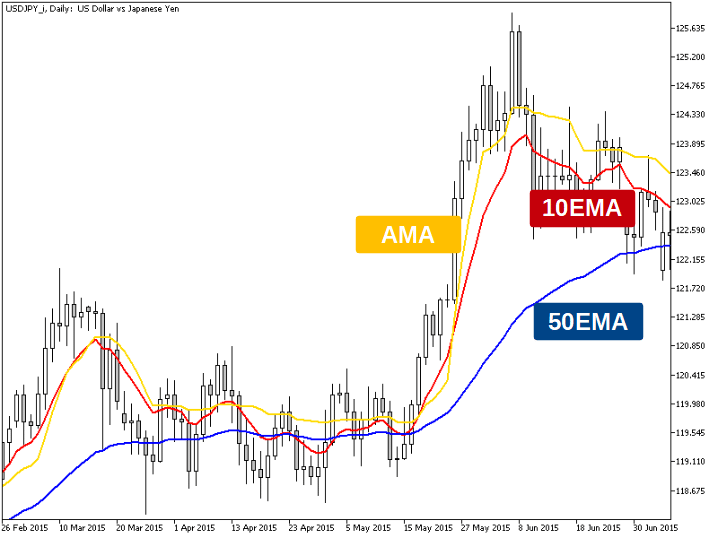
ちなみにMT5のAMAには期間、短期EMA、長期EMAという３つのパラメータがあります。上の例ではそれぞれ９、２、３０となっています。ただし、期間９はER[i]でトレンドを判定する期間Nのことです。短期EMA、長期EMAの期間は平滑化パラメータの上限と下限を決めるためのものです。通常の移動平均の期間とは意味が違うので注意してください。

以上、AMAの紹介でした。

ちょっと長くなってしまったので、その他の適応型移動平均については、別の記事で紹介します。