『Python実践データ分析100本ノック』ノック61

今回は、『Python実践データ分析100本ノック』で学んだことをアウトプットしていきます。

pulpとortoolpyライブラリのインストールに四苦八苦

pulpとortoolpyというライブラリを用いて、最適化計算を行うのですが、以下のようなエラーメッセージが表示されました…

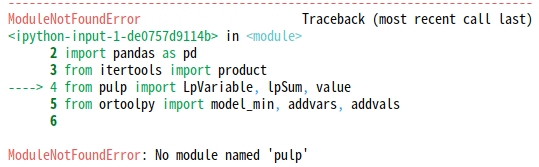
そこで、こちらを参考に、以下のコードをターミナルで実行してみました。

$conda install -c conda-forge pulp

すると、またもや、ModuleNotFoundErrorに遭遇…
今回は、ortoolpyモジュールが見つからないようです。

「condaにortoolpyをインストールすればいいや〜」と考え、以下のコードをターミナルで実行。

$conda install ortoolpy

しかし、インストールできない。
どうやら、ortoolpyは、condaでは提供されていないライブラリのようです。

こちらのサイトにしたがい、pipでインストールすることに。

$pip install ortoolpy

condaとpipを併用すると環境が壊れるということがあるようなので、できるだけcondaを使ってインストールし、condaで提供されていないライブラリのみ、pipでインストールするようにしています。（この方法が良いかどうかはわからないが）

自分も、これまでできるだけcondaを使ってインストールしてきただけに、今回は泣く泣く、pipでインストールする羽目になりました(T_T)

ノック６１：輸送最適化問題を解いてみよう

pulpとortoolpyというライブラリを用いて、いよいよ輸送最適化問題を解いていきます。前者は最適化モデルの作成を行う役割を、後者は目的関数を生成して解く役割を担います。

まずは以下のコードを動かしてみて、動作を確認してみます。

import numpy as np
import pandas as pd
from itertools import product
from pulp import LpVariable, lpSum, value
from ortoolpy import model_min, addvars, addvals

# データ読み込み
df_tc = pd.read_csv('trans_cost.csv', index_col='工場')
df_demand = pd.read_csv('demand.csv')
df_supply = pd.read_csv('supply.csv')

# 初期設定
np.random.seed(1)
nw = len(df_tc.index)
nf = len(df_tc.columns)
pr = list(product(range(nw), range(nf)))

# 数理モデル作成
m1 = model_min()
v1 = {(i, j):LpVariable('v%d_%d'%(i, j), lowBound=0) for i, j in pr}

m1 += lpSum(df_tc.iloc[i][j] * v1[i, j] for i, j in pr)
for i in range(nw):
   m1 += lpSum(v1[i, j] for j in range(nf)) <= df_supply.iloc[0][i]
for j in range(nf):
   m1 += lpSum(v1[i, j] for i in range(nw)) >= df_demand.iloc[0][j]
m1.solve()

# 総輸送コスト計算 
df_tr_sol = df_tc.copy()
total_cost = 0
for k, x in v1.items():
   i, j = k[0], k[1]
   df_tr_sol.iloc[i][j] = value(x)
   total_cost += df_tc.iloc[i][j] * value(x)
   
print(df_tr_sol)
print('総輸送コスト：' + str(total_cost))

ノック58で触れた通り、最適化計算は、目的関数と制約条件を定義できれば、解くことができます。上記のコードの「数理モデル作成」の部分では、それらを順番に定義しています。

m1 = model_min()

まず、1行目は、m1として「最小化を行う」モデルを定義しています。これから定義する目的関数を、制約条件のもとで「最小化」できます。

次に、m1に条件を加えることで、目的関数と制約条件を加えていきます。

v1 = {(i, j):LpVariable('v%d_%d'%(i, j), lowBound=0) for i, j in pr}
m1 += lpSum(df_tc.iloc[i][j] * v1[i, j] for i, j in pr)

この2行では、lpSumによって、目的関数をm1に定義します。

各輸送ルートのコストを格納したデータフレームdf_tcと、（これを変化させることで最適ルートを求める）主役となる変数v1とのそれぞれの要素の積の和によって、目的関数を定義します。

変数v1は、LpVariableを用いてdict形式で与えます。

そして、制約条件をm1に定義します。

for i in range(nw):
   m1 += lpSum(v1[i, j] for j in range(nf)) <= df_supply.iloc[0][i]
for j in range(nf):
   m1 += lpSum(v1[i, j] for i in range(nw)) >= df_demand.iloc[0][j]

制約条件もまた、lpSumを用いて与えることができます。ここでは、工場の製造する製品が需要量を満たすように、また、倉庫の供給する部品が供給限界を超過しないように制約条件を与えます。

これらによって与えた条件からなる最適化問題をsolveによって解きます。

m1.solve()

solveを実行することによって、変数v1が最適化され、最適な輸送コストが求められます。

以上、本書の「数理モデル作成」の解説は終了となりますが、それ以外の解説が載っていなかったので、「数理モデル作成」以外の部分を自分なりに調べてみました。

itertools.productで、複数のリストの直積（デカルト積）を生成する。

「初期設定」の部分で登場するitertools.product()について、調べてみました。参考にしたのはこちらのサイト。

直積（デカルト積）は、複数の集合から要素を一つずつ取り出した組み合わせの集合。例えば2つのリストがあったとき、すべてのペアの組み合わせのリストが直積。

引数に2つのリストを指定するとitertools.product型のオブジェクトが返る。itertools.product型はイテレータなので、それをそのままprint()しても中身は出力されない。

import itertools
import pprint

l1 = ['a', 'b', 'c']
l2 = ['X', 'Y', 'Z']

p = itertools.product(l1, l2)

print(p)
# <itertools.product object at 0x1026edd80>

print(type(p))
# <class 'itertools.product'>

forループで列挙。各リストの要素の組み合わせがタプルで取得できる。

for v in p:
   print(v)
# ('a', 'X')
# ('a', 'Y')
# ('a', 'Z')
# ('b', 'X')
# ('b', 'Y')
# ('b', 'Z')
# ('c', 'X')
# ('c', 'Y')
# ('c', 'Z')

list()でリスト化することも可能。タプルを要素とするリストとなる。

l_p = list(itertools.product(l1, l2))

pprint.pprint(l_p)
# [('a', 'X'),
#  ('a', 'Y'),
#  ('a', 'Z'),
#  ('b', 'X'),
#  ('b', 'Y'),
#  ('b', 'Z'),
#  ('c', 'X'),
#  ('c', 'Y'),
#  ('c', 'Z')]

本書のコードでは、list()でリスト化していましたので、prには、タプルを要素とするリストが格納されていることになりますね。

ここまでの説明では引数を便宜上「リスト」としてきたが、イテラブルオブジェクトであればタプルでもリストでもrangeオブジェクトでもなんでもいい。また、引数にはイテラブルオブジェクトを2個以上指定できる。

t = ('one', 'two')
d = {'key1': 'value1', 'key2': 'value2'}
r = range(2)

l_p = list(itertools.product(t, d, r))

pprint.pprint(l_p)
# [('one', 'key1', 0),
#  ('one', 'key1', 1),
#  ('one', 'key2', 0),
#  ('one', 'key2', 1),
#  ('two', 'key1', 0),
#  ('two', 'key1', 1),
#  ('two', 'key2', 0),
#  ('two', 'key2', 1)]

本書のコードでは、

pr = list(product(range(nw), range(nf)))

というように、rangeオブジェクトを引数にとっていますね。
prの中身を、pprintで表示させてみました。

import pprint
pprint.pprint(pr)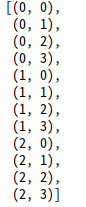

予想通り、タプルを要素とするリストが格納されていることが確認できました。

変数v1の定義における辞書内包表記

v1 = {(i, j):LpVariable('v%d_%d'%(i, j), lowBound=0) for i, j in pr}

まず、辞書内包表記に面食らってます^^;
こちらのサイトを参考にしました。

リスト内包表記でリストを作成するのと同様に、辞書内包表記で辞書を作成することもできる。リスト内包表記との違いは、[]でなく{}で囲むこと、および、キーと値の2つを指定すること。

{キー: 値 for 任意の変数名 in イテラブルオブジェクト}

l = ['Alice', 'Bob', 'Charlie']

d = {s: len(s) for s in l}
print(d)
# {'Alice': 5, 'Bob': 3, 'Charlie': 7}

次に、辞書の値である、「LpVariable('v%d_%d'%(i, j), lowBound=0)」の部分。理解できない…

変数（LpVariable）の作成

LpVairableの作成については、こちらのサイトを参考にしました。

変数とは、意思決定の対象です。具体例を上げてみましょう。

自宅から学校への最短路を求めたい場合の変数：各経路を通るかどうか
生産額を最大化したい場合の変数：製品ごとの生産量
輸送費用を最小化したい場合の変数：経路ごとの輸送量

PuLPの変数の種類は、以下の3種類あります。 線形最適化では、連続変数だけ使います。LpVariableは、デフォルトで連続変数になります。

連続変数：実数値を表す変数です。
0-1変数：0または1のみを表す変数です。
整数変数：整数値を表す変数です。

LpVariableのオプション
第1引数：変数名（必須）
lowBound：変数の下限。デフォルトはNoneで下限なしです。
upBound：変数の上限。デフォルトはNoneで上限なしです。
cat：変数の種類。デフォルトはpulp.LpContinuousで連続変数です。

LpVariableの作成例

LpVariable('x')：自由変数を作成します。自由変数とは、-∞から∞までの値を取ることができる変数です。
LpVariable('y', lowBound=0)：非負変数を作成します。非負変数とは、0から∞までの値を取ることができる変数です。
LpVariable('y', lowBound=0, upBound=1)：上下限のある変数を作成します。範囲は、lowBoundの値からupBoundの値までです。

LpVariableの注意事項

LpVariableは、必ず変数名を指定する必要があります。また、全ての変数は、異なる名前になっていないといけません。

ということは、「'v%d_%d'%(i, j)」は、第一引数で必須である、変数名である可能性が高そうです。

'v%d_%d'%(i, j)は、文字列の書式設定だった！！！

さらに検索してみると、Yahoo!Japan知恵袋で自分と全く同じ疑問にぶつかった人が質問されていました。

回答を見てみると…

文字列の書式設定になります。
>>> 'v%d_%d'%(5,10)
'v5_10'

文字列の書式だったのか〜！
一度学んだけど、ど忘れしておりました…

というわけで、こちらのサイトで復習。

書式化演算子の % を使用することで数値や文字列に対して書式を設定し新しい文字列を作成することができます。

数値に対する書式化は以下のようになります。

num1 = 30
result = "10進数では %d 、16進数では %x です" % (num1, num1)
print(result)

>> 10進数では 30 、16進数では 1e です

数値が入った変数をそれぞれ 10 進数と 16 進数に変換し、変換した値をベースとなる文字列の指定した位置に挿入した新しい文字列を作成しています。

lpSumで、変数の和を高速計算

lpSumについて検索。
こちらのサイトを参考にしました。

（pulpにおいて;註）変数の和を表現するときにsumよりもlpSumを使った方が高速にプログラムが動くという話です。

総輸送コスト計算の中身を吟味

# 総輸送コスト計算 
df_tr_sol = df_tc.copy()
total_cost = 0
for k, x in v1.items():
   i, j = k[0], k[1]
   df_tr_sol.iloc[i][j] = value(x)
   total_cost += df_tc.iloc[i][j] * value(x)
   
print(df_tr_sol)
print('総輸送コスト：' + str(total_cost))

総輸送コスト計算のコードをよく見ていくことにします。
こちらのサイトを参考にしました。

結果はitems()で取得できる。
kに変数名の引数(この場合、座標)、xに計算された数量が入る

viは辞書オブジェクト（dict形式）として定義したので、items()で取得できるのかなと考えます。辞書のキーはタプルですね。

ふう。
今回のノックは実にヘビーでした…