
[Rによるデータ分析入門]離散選択モデルの様々(3):ヘーキットモデル
ヘーキット・モデルとは、被説明変数が観察されるのが一部、というような状況に用いられるモデルです。本コラムでは、数学的な説明は計量経済学のテキストに譲り、できるだけ直感的な説明でヘーキットの意義について説明した後、Rにおける推計方法を紹介します。
なお、このシリーズを通しで読みたい方は以下を参照してください。
ヘーキットの直感的な意義
たとえば、健康状態と賃金の関係を考えてみましょう。今、データには健康状態が悪くて非就業の人と健康状態が良くて就業している人が含まれているとします。このとき賃金が観測できるのは一定以上の健康水準で就労している人に限られます。このようなときに就業している人だけで、健康状態と賃金の関係を計測しようとすると係数が正しく測定できない可能性があります。
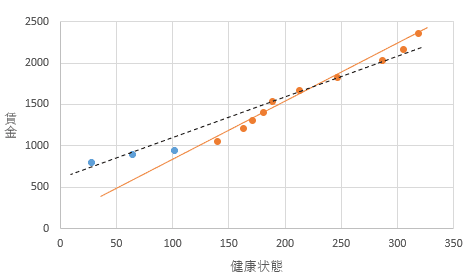
これを次の図を用いながら考えましょう。図のオレンジの点は就業している人の賃金と健康状態を示します。一方、健康状態が悪くて就労していない人は、実際は「企業から低い賃金を提示されたが、割に合わないと考えて非就業を選択している」と考えます。ここで企業から提示された賃金(提示賃金)は観察されませんが、この図には非就業者の提示賃金が青の点で示されています。
ここでオレンジの線は、観察される賃金と健康状態の点に対して近似線をひいたものです。一方、黒の点線は観察されるオレンジの点と観察されない青の点を含めて近似線を引いたものです。就業していない人は提示された賃金がひくいので就業していないとすれば、黒の近似線が本来の健康状態と賃金の関係ということになります。この図では、観察されるデータだけで引いたオレンジの近似線と、提示賃金を含む点を含めて近似線を引いた黒の線で傾きが異なっていることがわかります。このような場合、観察値だけで引いたオレンジの近似線の傾きには偏り(バイアス)があると考えます。
ヘーキットでは人々の就業/非就業の意思決定をモデル化することで、傾きの偏り(バイアス)を補正する手法です。
トービットモデルとの違い
ここでトービットモデルとの違いについて考えておきましょう。トービットモデルの場合、ある一定の条件で被説明変数がゼロなどの特定の数値をとり、そこから変わらないような状況で用いられます。たとえば所得と自動車の購入台数を考えると、所得が高くなると所有台数が増えますが、逆に所得が一定程度低くなると所有台数はゼロになり、そして、それよりも所得がいくら低くても所有台数はマイナスになることはなくゼロのままになります。次のグラフは健康状態と労働時間の関係を示していますが、健康状態が一定水準を下回ると労働時間はゼロになりますが、マイナスになることはありません。
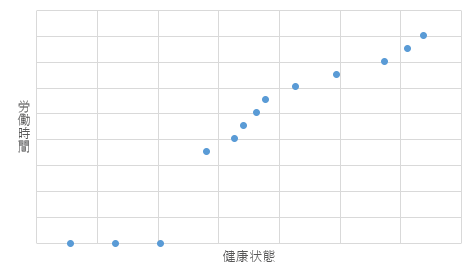
トービットとヘーキットもいずれも、ある条件で被説明変数が特異な動きをとるのですが、最大の違いはトービットでは被説明変数がすべて観測されているのに対して、ヘーキットでは被説明変数が観察されないという点にあります。ヘーキットは「被説明変数が観察されない」という状況を考慮して傾きを補正する推計方法になります。
ヘーキットモデルの数式表現
ここでは山本 (2015)の表現を借りつつ、ヘーキットモデルの数式表現をみてみましょう。まず、$${Y_i }$$を賃金、$${M_i }$$を就業していれば1をとるダミー変数とします。$${Y_i }$$が観察されるのは$${M_i }$$が1のときだけですので、これを以下のように表します。
$$
Y_i=a+bX_i+u_i if M_i=1\\
. (unobserved) if M_i=0 \\
$$
一方、就業するかどうかはprobit/logitのときと同様に潜在変数mよりも$${M_i^*}$$が大きければ就業、小さければ非就業となります。
$$
M_i =1 if M_i^* >m \\
M_i=0 if M_i^* \leq m
$$
つまりヘーキット・モデルは、まず就業・非就業の意思決定をprobitで推計し(第一段階)、就業していれば賃金$${Y_i }$$が観察されるので観察されるサンプルで賃金の決定要因を分析します。
推計式の導出など、ここから先の議論はテクニカルになるので説明は他書に譲りますが、第二段階の推計式には、第一段階のプロビットの推計結果から計算される逆ミルズ比(Inverse Mills ratio)を二段階目の説明変数に導入することで賃金関数の傾きを補正します。逆ミルズ比とは第二段階の被説明変数の「観察されにくさ度合」を示す変数で、この係数は第1段階と第2段階の推計式の誤差項の相関を示すので、この係数が有意であれば1段階目を無視することによるサンプル・セレクション・バイアスが発生していると解釈します。なお、後述する最尤法でヘーキット・モデルを使うと逆ミルズ比は出てこないのですが、第1段階の誤差項と第2段階の誤差項の相関を示すρが推計されるので、この係数が有意であるかどうかサンプル・セレクション・バイアスが発生しているかを判断します。
この補正により図1のグラフのように黒の点線の近似線の傾きを計算する、というのがヘーキット・モデルの仕組みです。なお、第一段階をプロビットで推計し、そこから計算した逆ミルズ比で第二段階を推定する方法(ヘックマンの二段階推定法とも呼びます)と、第一段階の式と第二段階の式を最尤法で同時推定する方法がありますが、後者のほうが望ましい性質を持つことが知られています。
一つ、注意事項として、ヘーキットモデルを推定する際には、第一段階の説明変数には第二段階の説明変数に含まれていない変数を最低一つ入れるべきであるという除外制約(exclusion restrictions)があります。上記の例では就業/非就業の意思決定には影響するが賃金には影響しない変数を用意する必要があります。
Rによる推計方法
Rでヘーキットモデルを推定するには{sampleSelection}パッケージをインストールし、library(sampleSelection)で呼び出しておく必要があります。ヘーキットモデルはhekit()関数を使います。使い方は以下の通りです。
hekit(selection=M~x1+x2+x3, outcome=Y~x2+x3, data=データオブジェクト, method="ml")
MはYが観察されるときに1をとるダミーでselection=で第一段階の推計式を特定しています。Yが第二段階の被説明変数で、outcome=で推計式を示しています。説明変数のx1は第一段階の推定式には含まれますが、第二段階の推定式には含まれない変数になっていて、除外制約を満たされていることがわかります。
なお、method=”ml”を指定することで第一段階の式と第二段階の式を同時推定しています。ここを"2step"にすると、まず第一段階を推定して逆ミルズ比を計算し、次に第二段階を推定する二段階推定法が実施されます。
分析事例(1)
最初に紹介する事例で使用するのは{wooldridge}パッケージに含まれるmrozです。このデータで賃金関数を推計し、教育年数が1年延びると賃金がどの程度変化するかを見てみましょう。被説明変数は賃金wage、説明変数には教育年数educ、経験年数とその二乗exper, exper^2を入れます。このデータは、753人中428人が就業女性、325人が非就業女性になります。つまり、325人については就業していないので賃金のデータが観測されてない、というデータ構造になっています。なお、第一段階の推計式には教育年数、経験年数に加えて、妻の所得nwifeinc、6歳未満の子供ダミーkidslt6、6歳以上の子供ダミーkidsge6が含まれています。
サンプルのコードも置いておきます。
まず、最小二乗法による推定結果です。
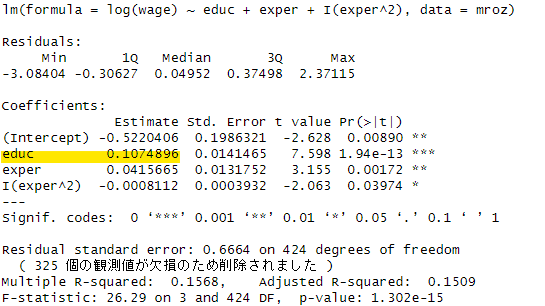
このときのeduc教育年数の係数は0.107でした。
次に最尤法による同時推定のヘーキットモデルの推定結果です。educの係数は0.1093で微妙に大きくなっているが、あまり大きな違いはみられませんでした。緑でハイライトしたsigma(第2段階の推計式の誤差項の分散)は有意ですが、rho(第1段階と第2段階の相関係数)は有意ではなく、1段階目と2段階目の推計に関連性がみられないため、2段階目だけを最小二乗法で推計したものと、最尤法のヘーキット・モデルの結果がほぼ同じになっていると解釈できます。

最後に最尤法(method="ml")による推定結果と2段階推定(method="2step")による推定結果を比べてみましょう。以下は二段階推定法の結果です。
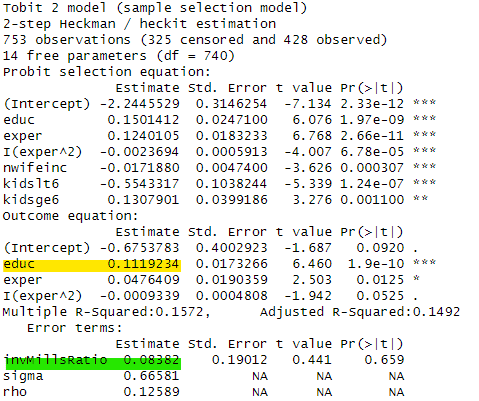
二段階推定では、educの係数が0.119と最小二乗法よりもやや係数が大きくなりましたが、劇的な変化とまではいえません。また、緑でハイライトしたinvMillsRatioの係数は有意ではないので1段階目の推計式と2段階目の推計式の関連は薄く、サンプルセレクションの影響は少ないと言えそうです。
分析事例(2)
ここで紹介するのは Cameron and Trivedi (2005)の第16章6節(16.6)で紹介されたの医療保険と医療費支出の関係についての分析例です。このデータはDeb and Trivedi (2002)による社会実験で得られたデータで、個人レベルの医師訪問回数、健康状態や家族属性、医療保険の状況に関するデータが含まれています。興味深いのは、この社会実験では、医療保険はランダムに指定されたものに加入するように促されており、「個人が医療保険を自発的に選択する可能性」を排除しているので、医療保険のカバー率などを外生変数とみなせるという点にあります。
この事例では第二段階目の推定式のYは病院での医療費支出ですが、この変数は、通院しなかった人については観察されません。そこで、第一段階を通院するかどうかのダミー変数を、第二段階は医療費支出を被説明変数とするヘーキット・モデルを推定します。
説明変数としては以下のような変数を用います。
logc:医療費の自己負担率(1-医療保険のカバー率)
hlthg: 自己申告の健康状態・良好ダミー
hlthf: 自己申告の健康状態・中ぐらいダミー
hlthp: 自己申告の健康状態・不良ダミー
linc: 所得(対数値)
educdec: 教育年数
xage: 年齢
female: 女性ダミー
child: 子ども有
black: 黒人ダミー
被説明変数は
binexp: 第一段階、通院するかどうかのダミー変数
lnmeddol: 第二段階、医療費支出(対数値)
※ Cameron adn Trivedi (2005)では、多くの変数をコントロール変数として加えられていますが、本コラムでは簡略化のため変数の数を制限しています。
まず最小二乗法の結果です。今、関心のある変数は医療費の自己負担率(logc)です。黄色でハイライトした係数はマイナスですので、自己負担率が高くなると「通院控え」が起こるので医療費が抑制されることがわかります。
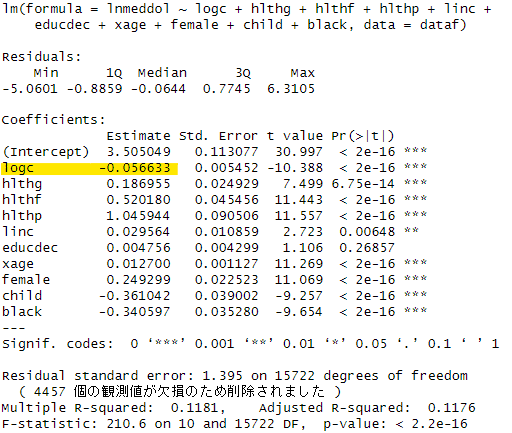
次に最尤法によるヘーキット・モデルの推計です。スクリプトは以下の通りです。
result2 <-heckit(selection=binexp~logc +hlthg+hlthf+hlthp+
linc+educdec+xage+female+child+black,
outcome=lnmeddol~logc +hlthg+hlthf+hlthp+
linc+educdec+xage+female+child+black,data=dataf, method="ml")結果は以下に示されています。まず、第一段階の推計式と第二段階の推計式の誤差項の相関を示すrho(緑でハイライトされています)をみると、今度は0.71と大きな値で統計的にも有意になりました。よってサンプル・セレクション・バイアスが発生していると考えられます。一方、黄色でハイライトしたlogcの係数はマイナスですが、係数の大きさが最小二乗法の-0.056から、ヘーキット・モデルでは-0.096に大きくなっていることが分かります。

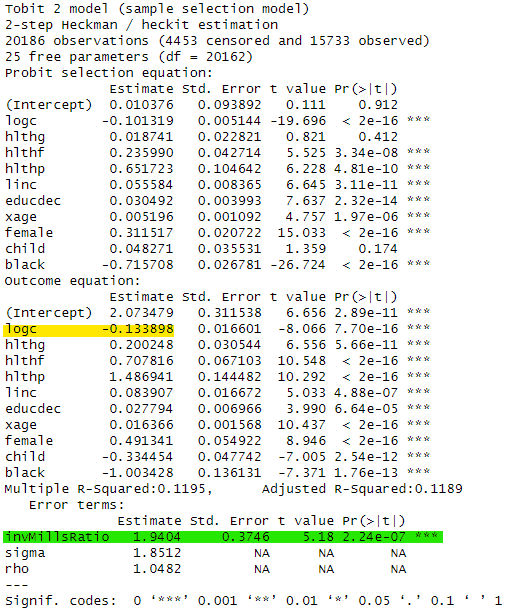
次に二段階推定法です。スクリプトは以下の通りです。
result3 <-heckit(selection=binexp~logc +hlthg+hlthf+hlthp+
linc+educdec+xage+female+child+black,
outcome=lnmeddol~logc +hlthg+hlthf+hlthp+
linc+educdec+xage+female+child+black,data=dataf, method="2step")結果についても見ておきましょう。緑でハイライトしたinvMillsRatioの係数は統計的に有意になったのでサンプル・セレクション・バイアスが発生していると読むことができます。一方、logcの係数は-0.133と最小二乗法の係数よりも絶対値で大きくなっていることが確認できます。
次の離散選択モデルの様々(4)ではカウントデータに用いられる推定法を紹介します。
本コラムは「Rによるデータ分析入門」のWEBサポートページとして作成されました。WEBサポートの一覧は以下を参照してください。
WEBサポートの一覧は以下を参照してください。
この記事が気に入ったらサポートをしてみませんか?
