
高校数学の参考書・問題集ひたすら解いてみる(その8)因数分解(4)
えー、私の記事に『好き』していただいた方々がいらっしゃいまして
とってもありがたいです。
なんだかんだいって嬉しいですね。
この場をお借りしてお礼いたします。
さて、今回は参考書・問題集にある問題を解かずに
因数分解の解き方についてのお話ししたいと思います。
そういえばたすき掛け
因数分解といえば『たすき掛け』ってありますよね。
でも私の解き方で『たすき掛け』っぽいこと書いてないんですよ。
(自分でもそう思ったんですけど)
で、我流になっちゃうかもしれないんですけど
自分の頭のなかでどういう思考回路で因数分解を解いているか、
可能な限りで書いてみようと思います。
2次3項式の因数分解(その1)
2次3項式の因数分解で2次の項の係数が1の時の
因数分解をしてみます。
例題は超簡単に以下とします。
$${x^2+3x+2}$$
ではどんな風に思考しているか図示してみます。
手順は丸数字のとおりです。

どうですか?わかりますかね?
2次3項式の因数分解(その2)
今度は2次3項式の因数分解で2次の項の係数が1以外の時の
因数分解をしてみます。
例題は超簡単に以下とします。
$${6x^2+x-15}$$

うーん、うまく書けてるのかなぁ?
と思いつつ、こんな手順でやってます。
ちなみに$${x}$$の項は③の変形では$${\{2\times5+3\times(-3)\}x}$$って
書くべきなんでしょうけど省略してます。(わかりづらいし…)
ちなみに②のタイミングでは組み合わせの総当たりはしていません。
明らかに違う組み合わせは直観的にわかるので…(ほんとは説明を書くのが面倒になってきたので…)
で、ですよ。
この内容を参考書とか見ると
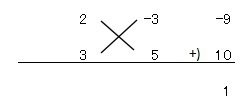
なんと、一手で書いちゃってます。すげーっ!
まぁ、慣れてしまえばこっちの書き方のほうが楽だし、
いちいち手順書かれてもねぇという気もします。
ただ、最初の最初だけはもう少し丁寧に書いても
いいんじゃね?とも思います。
さて、因数分解も4回やったのでそろそろいいかなと
思いました。
次回からは同じ章節は3回をMAXで書いていきたいと思います。
(気が向いたら4回か5回まで…まぁ5回が最高としておこうかな)
ということで次回からは新しい章節に入りたいと思います。
でわまた。
この記事が気に入ったらサポートをしてみませんか?
