OpenSeesPyを用いた梁要素の線形座屈解析 -その1線形座屈荷重の算出-

2024年2月24日 00:10

はじめに

やぶうちと申します。
北九大の藤田研究室で行っていたデジラボを研究室卒業後も個人でマイペースに続けたいという考えから、今回の記事の執筆に至りました。
藤田研のNoteは下記リンクから閲覧可能です。

初投稿ということで、ネタに困ってしまったので本記事では私が修士論文で使用した構造解析プログラムの説明をします。
「その1」では、構造物の線形座屈荷重の算出プログラムを構築します。
「その2」では、本記事で構築したプログラムをもとに構造物の線形座屈モードをMatplotlibを用いて描画するプログラムを執筆する予定です。
拙い点も多々あるかと思いますがご一読いただければ幸いです。

解析概要

線形座屈解析とは増分外力に伴う変形を考慮せず、線形剛性と幾何剛性を用いて構造物の座屈荷重の概算値を算出する構造解析手法のひとつです。
ここでは当該解析手法をカリフォルニア大学バークレー校がオープンソースとして公開している有限要素解析フレームワークであるOpenSeesを用いて行うこととします。
ただし、線形座屈解析は一般固有値問題として解かれることが一般的であり、有限要素解析とは解法が異なるため、OpenSees上で直接的にその解析の設定を行うことはできないようです。

したがって、ここでは剛性行列の算出をOpenSees、一般固有値問題の計算にはPythonの科学計算ライブラリであるSciPyを用いて解くこととします。
また、解析対象物は3次元梁要素としてモデル化します。
ここでは以下に示す片側に1.0kNの圧縮力を受ける20分割された長さ1.0mの柱をプログラム説明のための解析対象物とします。
自重の考慮はここでは行いません。
支持条件は単純支持です。

線形座屈解析プログラムの作成

プログラムの実行環境は下記の通りです。
環境によってはimport openseespy.preprocessing.DiscretizeMemberの部分でエラーが生じるようですのでご注意下さい。

C:\Users\User>python -V
Python 3.8.8
C:\Users\User>pip list
openseespy 3.3.0.1.1

なお、ここで紹介するプログラムは下記リンクを参照して構築したものです。
Right Under Your Nose – Portwood Digital

はじめに、下記のモジュールをimportします。
各モジュールの主な役割を以下に箇条書きで示します。

Numpy･･･リストを昇順に入れ替える、または配列をnp.array形式にする
SciPy･･･固有値問題の計算
openseespy･･･本記事で使用するメインの構造解析ソルバー

import numpy as np
import scipy.linalg as slin
import openseespy.opensees as ops
import openseespy.preprocessing.DiscretizeMember as dm

下記のように解析対象物の設定をします。
各記号の定義を以下に箇条書きで示します。

r：x,y,z軸節点座標ベクトル
ij：要素節点関係
E：ヤング率
G：せん断弾性係数
A：断面積
Iy：y軸断面二次モーメント
Iz：z軸断面二次モーメント
J：ねじり定数

# 節点座標と要素節点関係
r,ij=[],[]
x=np.arange(0.0,1.05,0.05,dtype=float)
for i in range(len(x)):
	r.append([x[i],0,0])
for s in range(len(x)-1):
	ij.append([s,s+1])
r,ij=np.array(r,dtype=float),np.array(ij,dtype=int)

# 各種構造特性係数
E,A,Iy,Iz,G,J=205000.0, 0.01, 8.33e-06, 8.33e-06, 102500.0, 1.40e-05

#ベクトルaをb回りに角度theta回転させる
def rotation(a,b,theta):
	rad=np.radians(theta)
	c,s=np.cos(rad),np.sin(rad)
	b=b/np.linalg.norm(b)
	b1,b2,b3=b[0],b[1],b[2]
	m=np.array([
	[c+b1**2*(1-c),b1*b2*(1-c)-b3*s,b1*b3*(1-c)+b2*s],
	[b2*b1*(1-c)+b3*s,c+b2**2*(1-c),b2*b3*(1-c)-b1*s],
	[b3*b1*(1-c)-b2*s,b3*b2*(1-c)+b1*s,c+b3**2*(1-c)]
	],dtype=np.float64)
	return np.dot(m,a)
#部材座標ベクトルの作成
def make_local_coordinates(m,r,ij):
	l_vec,l_vecz=np.zeros((m,3),dtype=np.float64),np.zeros((m,3),dtype=np.float64)
	for e in range(m):
		i,j,theta=ij[e,0],ij[e,1],0
		x=r[j]-r[i]
		if x[0]==0 and x[1]==0:
			y=rotation(x,np.array([0,1,0],dtype=np.float64),90)
			z,z0=rotation(y,x,90+theta),rotation(y,x,90)
			l,l0=z/np.linalg.norm(z),z0/np.linalg.norm(z0)
			l_vec[e],l_vecz[e]=l,l0
		else:
			y=rotation(x,np.array([0,0,1],dtype=np.float64),90)
			y[2]=0.0
			z,z0=rotation(y,x,90+theta),rotation(y,x,90)
			l,l0=z/np.linalg.norm(z),z0/np.linalg.norm(z0)
			l_vec[e],l_vecz[e]=l,l0
	return l_vec,l_vecz
l_vec,l_vec_z=make_local_coordinates(len(ij),r,ij)

なお、使用部材は100×100mmの矩形断面を有する鋼材を想定した数値としていますが、そのあたりは自由に設定していただいて結構です。

# OpenSeesの解析条件
ops.wipe()
ops.model('BasicBuilder', '-ndm', 3)

# 節点座標の設定
for i in range(len(x)):ops.node(i+1,r[i,0],r[i,1],r[i,2])

# 境界条件の設定
ops.fix(1, 1, 1, 1, 0, 0, 0)
ops.fix(21, 0, 1, 1, 0, 0, 0)

# 梁要素と各要素に使用する材料の設定
for e in range(len(ij)):
	i,j=int(ij[e][0]+1),int(ij[e][1]+1)
	ops.geomTransf('Corotational',e+1,l_vec[e][0],l_vec[e][1],l_vec[e][2])
	ops.section('Elastic',e+1,E,A,Iy,Iz,G,J)
	ops.beamIntegration('Lobatto',int(e+1),1,1)
	dm.DiscretizeMember(i,j,1,'elasticBeamColumn',e+1,e+1,e+1,e+1)

# 解析の諸条件
ops.system('FullGeneral')
ops.numberer('RCM')
ops.constraints('Plain')
ops.test('NormUnbalance',1e-8,10000,0,1)
ops.algorithm('Newton')
ops.integrator('LoadControl',0)
ops.analysis('Static')

下記のように剛性行列を算出します。
ops.printA('-ret')
の部分で剛性行列の算出を行っています。

# 線形剛性行列Kl
ops.analyze(1)
N = ops.systemSize()
Kl = ops.printA('-ret')
Kl = np.array(Kl)
Kl.shape = (N,N)

# 幾何剛性行列Kg
ops.timeSeries('Constant',1,'-fact',1.0)
ops.pattern('Plain',1,1,'-fact',1.0)
# 荷重条件
ops.load(21, -1, 0.0, 0.0, 0.0, 0.0, 0.0)
ops.analyze(1)
N = ops.systemSize()
Kg = ops.printA('-ret')
Kg = np.array(Kg)
Kg.shape = (N,N)

ここで、線形座屈解析の結果から正の最小固有値を算出する下記の関数定義を行います。

# 線形座屈解析結果の正の最小固有値を取り出す
def sortModels(lam,x):
	# sort lambda and x
	lambda_sorted = np.sort(lam)
	lambda_inds = lam.argsort()
	x_Sort = np.zeros_like(x)
	for count,index in enumerate(lambda_inds):
		x_Sort[:,count] = x[:,index]
	# only modes with positive lambda
	index=0
	while index<len(lambda_sorted) and lambda_sorted[index]<0:
		index += 1
	lamSort = lambda_sorted[index:]
	x_Sort = x_Sort[:,index:]
	return lamSort,x_Sort

上記で求めた線形剛性行列と幾何剛性行列から接線剛性行列を求め、線形座屈荷重係数と線形座屈モードを算出します。

# 接線剛性行列Kt
Kt = Kl - Kg
lam, xi = slin.eig(Kl,Kt)
lamSort = np.sort(lam[lam>0])
lam,xi = sortModels(lam,xi)
lam,xi = np.array(lam,dtype=float),np.array(x,dtype=float)

上記のうち、"lam"が線形座屈荷重係数、"xi"には線形座屈モードが次数1から順に格納されています。
print(lam[0])
と宣言することで次数1の線形座屈荷重係数が出力されます。
3次までの線形座屈荷重係数は下記の通りとなりました。

1次：16.64736772
2次：64.32268575
3次：138.75986093

解析結果の妥当性判断

ここで、解析結果の妥当性判断を行いましょう。
今回は解析対象物が非常に単純ですので、下記のオイラー式によって線形座屈荷重を得ることが可能です。

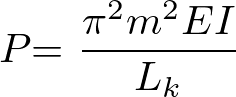
Pは線形座屈荷重、πは円周率、mは座屈モード次数、Eはヤング率、Iは断面二次モーメント、Lkは座屈長さ(単純支持より1.0)です。
オイラー式により得られた3次までの線形座屈荷重は下記の通りとなりました。

1次：16.86
2次：67.44
3次：151.74

前述した解析プログラムの数値とあまり誤差がないことが確認できます。
したがって、本解析プログラムによる解析は妥当であると考えます。

その2では本記事でのプログラムにより得られた線形座屈モード"xi"を用いて構造物の座屈モードを描画します。

この記事が気に入ったらサポートをしてみませんか？