
【岡山 塾 高校生 大学受験】大阪大学2024物理解答・解説
お世話になります。岡山駅東口徒歩5分、理系に強い予備校・岡山進学研究塾です。今回は2024年大阪大学物理大問1の解説と解答になります。

岡進研HPは画像をクリック

1週間無料で体験してみよう!
大阪大学2024物理
国立2次の物理は東京大学を筆頭にここ数年で問題量が増加する傾向が出ています。共通テストのように多くの情報量を時間内に処理するという社会人に求めることを10代の方に求めるという思想です。今年は大問IとIIがロングになっていますが、理解2科目で試験時間が150分と時間的に余り猶予はないかと思います。解けそうにない問題には見切りを付けるのも一つの手です。
パートI
問題はこちら。

ひもの張力が作用した瞬間に運動の向きが変わる
解き始める前に少なくともここまでは理解しておくこと。
・PとQは弾性衝動の為、1回目の衝突後は相対速度v1で反対方向に運動する。
・紐の張力が作用する瞬間はPとQが互いに内側の向きに張力が発生する。これにより、運動の向きが変わる。
・その後、2回目の衝突に至る。
・PとQの力学的エネルギーは保存される。
↓
「ああ、解いてみれば単振動のような周期運動になるんだろうな…」
衝突後の速度、ひもの張力が作用した直後の速度は実際に解けば分かります。その結果をもって、その先が分かればいいんです。
問1
反発係数が-1、P,Qの運動量が保存されることから、
衝突後のPとQの速度をv1'、v2'とすると、
(v1'-v2')/(v1-0) = -1 …… ①
mv1'+cmv2' = mv1 …… ②
①、②より
v1'=(1-c)v1/(1+c) …答え
v2'=2v1/(1+c) …答え
問2
ひもの張力が作用する前後でPとQの運動量と力学的エネルギーは保存されることより、ひもが張った直後の両者の速度をv1"、v2"とおくと、
mv1"+cmv2"=mv1'+cmv2'=mv1 …… ①'
mv1"^2/2+cmv2"^2/2=mv1’^2/2+cmv2’^2/2=mv1^2/2 …… ②'
①'と②'より
v2"= 0、2v1/(1+c)
(ⅰ) v2"= 0のとき
v1"= v1

(ⅱ) v2"= 2v1/(1+c)のとき
v1"= -(1-c)v1/(1+c)

問題文から(ⅱ)の場合は2回目の衝突が生じることはないので不適。
よって、
v1"= v1 …答え
v2"= 0 …答え
問3
問2までの結果より、Qから見たPの相対運動は
1回目の衝突から紐が張るまでは等速v1で離れる方向に距離lだけを移動し、
紐が張ってから2回目の衝突までは等速v1で接近する方向に距離lだけ移動する。よって、求める時間は
2l/v1 …答え
問4
訂正が出ています。

※ 元の問題文の書き方でいくと、
pとQの重心位置をそれぞれ求めよ。
訂正後でいくと
PとQを一体化した状態での重心位置を求めよ。
(全くちゃいまんがな…)
加えて、この問いが絶対座標系か相対座標系かによっても答えは全く別物となります。ここでは相対座標系(Qから見たPの座業系、つまりQのx座標を0として考察した結果とします)
つまり、PとひもとQを一纏めにして、2物体系として処理すれば良いのです。

時刻tにおけるPの位置をxp、Qの位置をxqとする。Qから見たPの位置をXとすると、
X=xp-xq …③
(ⅰ)PがQから離れるとき、③より
xp-xq=X=-v1、
xq=2v1t/(1+c)よりxp=(1-c)v1t/(1+c)
PとQの重心位置をxgとおくと、
xg=(xp+c・xq)/(1+c)より
xg=v1t/(1+c)
(ⅱ)PがQに接近するとき
Qの位置は固定なので、相対座標系で解くならxq=0としても問題ない。
xp=v1t、xq=0として
(ⅰ)と同様に
xg=v1t/(1+c)
以上、(ⅰ)(ⅱ)よりいずれの場合も解は
xg=v1t/(1+c)となる … 答え
※ 絶対座標系で解いても構いませんが、
ブログの記事が長くなり過ぎる懸念があり、機会があれば別解としてご紹介しようと思います。ご了承ください。
パートⅡ
問題はこちら。

〈解き始める前に〉
パートⅠとのモデル比較をしてみてください。
2次の物理は(化学もですが)同じ大問の前半と後半でモデル比較をすることで、構図が理解しやすくなることが多々あります。この場合は
Ⅰ:は張力が作用する瞬間以外はPとQに力は作用しない。
Ⅱ:Qにはバネが自然長のとき以外、常にバネによる復元力が作用している。PについてはⅠと同様。
(ちなみに、Ⅱを解くにはそこまで比較にこだわなくとも解けます)
問5
・Qの運動は1回目の衝突後、バネで連結された単振動となる。
・衝突前にPの持つ運動エネルギー(運動エネルギー)は衝突後、一部(場合により全て)Qの弾性エネルギーとなる。
衝突後のPとQの速度をvp、vqとして両者が弾性衝突であること、運動量が保存されることより、
(vp-vq)/(v2-0)=-1
Mvp+Mvq=Mv2
→ vq=v2、vp=0
ここで2回目の衝突がx=0(1回目の衝突と同じ位置)で起こる条件が分かる
【2回目の衝突が1回目と同じ位置で起こるための条件】
vp、vqの計算結果より、題意を満たすには
ひもの長さlは単振動の振幅Aよりも長くある必要がある。
(→ lがAよりも短いと、衝突後バネが縮み切るより先に張力が作用し、Pが動くため、2回目の衝突が同じ位置で起こらない)
力学的エネルギー保存則より、題意を満たす最小長さをl0とすると
(1/2)Mv2^2=(1/2)k(l0)^2
→ l0=v2√(M/k) … 答え
問6
単振動の周期をT、固有振動数をωとすると、
v2=l0・ω、ωT=2πより
T=2π・√(M/k)、
2回目の衝突が起こるまでの時間は2T/4(=T/2)より、
T=π・√(M/k) …答え
問7
2回目の衝突直後のPとQの速度をvp'、vq’とすると、
(vp'-vq’)/(0-v2)=-1 … ④
運動量保存則より
Mvp'+Mvq'=Mv2 … ➄
④、➄より
vp'=v2、vq'=0
2回目衝突後から3回目衝突までの時間は問3と同様に考えて良いので、要した時間は 2l/v2、
3回目までの衝突に要した時間は
…⑥
3回目の衝突から(2n+1)回目までの衝突は⑥をn回繰り返せば良いので、求める時間は
n・(π・√(M/k)+2l/v2) … 答え
パートⅢ
問題はこちら。
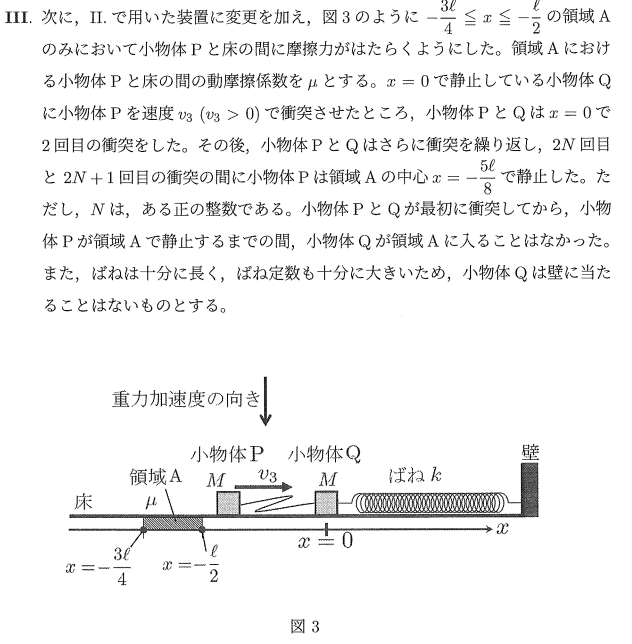
【Ⅱとの比較】
x=-l/2から-3l/4の間を1回通過するたびにμMg・(l/4)だけ力学的エネルギーを損失する。摩擦力のした仕事量の合計値が初期の力学的エネルギー((1/2)Mv3^2)と同等になった時点でPは停止する。それ以外はⅡと同様であるが、エネルギーを損失するたびに、Pの動く範囲は減少することには注意すること。
【注意】
初期条件として、Pが動き始める位置が領域AよりもQに近い位置か、遠い位置かの記載がされていない。
(図3の状態より前者であろうが、言葉で明確に記載はされていない)
問8
Pがxの負の方向に進行中に停止した場合と正の方向に停止した場合とで場合分けする必要が有る。
(ⅰ)Pがxの負の方向に移動中に停止した場合
停止するまでに合計で(N-1)往復し、さらにl/8だけ領域Aを移動して停止したことになるので、
μMg(2(N-1)・l/4+l/8) = (1/2)Mv3^2
→ 4v3^2/(4N-3)・gl …答え
(ⅱ)Pがxの正の方向に移動中に停止した場合
μMg(2(N-1)・l/4+3l/8) = (1/2)Mv3^2
→ 4v3^2/(4N-1)・gl …答え
総評
力学としては周期性を見抜いて解く良問と言える。しかし、問題文に明確な条件指定がなく受験生に混乱を招きかねない(と言うより招きます)出題は大学として本来あってはならないことである。科目問わず、言語で条件・状況を正しく相手に伝えることは非常に重要なことですから。計算量はさほど大したものではないので、力学モデルから構図を見抜き短時間で完答したい問題である。
まとめ
岡山進学研究塾では2024年度より数学と物理限定で3名から5名程度での集団講義を実施いたします。各科目¥12,000/月と大学受験としては破格の安価となっております。講義では原理・原則を理解できるように丁寧に解説し、演習では定義に基づいた解法に重点を置いています。
お問い合わせは
Tel 086-207-2450
E-mail study_support@okashinken.com
までお気軽にどうぞ。
〒700-0023
岡山市北区駅前町1丁目7-22カタヤマビル5F
岡山進学研究塾
