
特殊直交行列を解説!!
$${特殊直交行列T=\dfrac{1}{3}\begin{pmatrix}-1&2&2\\2&-1&2\\2&2&-1\end{pmatrix}に対してf_T:\mathbb{R^3}\to\mathbb{R^3},f_T(\vec{x})=T\vec{x},(\vec{x}\in\mathbb{R^3}) }$$は回転を表す.この回転の回転軸の$${方向ベクトル\vec{l}と回転角\thetaの余弦\cos\thetaを求めよ.}$$の問題を解説します。
f(x)の使い方
変化前と変化後
$${f_T(\vec{x})}$$について、使い方が理解できるようになれば、問題は解決します。ここで分かりやすくするために、$${f_T(\vec{x})=\vec{y}}$$と置きます。
イメージは、$${\vec{x}}$$は変化前、$${\vec{y}}$$は変化後と考えてください。中学生のときに、関数というものを扱いましたよね。$${y=ax}$$のようなものです。$${x}$$に$${a}$$を掛け算することで$${y}$$になりますよね。
実はy=ax
今回の問題では$${\vec{y}=T\vec{x}}$$という一次関数のようなものです。
すなわち、$${\vec{x}}$$に$${T}$$というもの(特殊直行行列)を掛け算することで$${\vec{y}}$$に変化するのです。
なので、問題文で$${f_T(\vec{x})=T\vec{x}}$$と書いてあるのです。
図形的意義
マシュマロ焼き
特殊直交行列を実際に、立体的に考えましょう。普通の関数では、単に〇倍になるなどの変化ですが、今回の関数は変化させる方法が少し特殊です。
特殊直交行列は軸を回転させて変化させます。イメージはマシュマロ焼きです。楊枝を軸にしてマシュマロを刺して、ころころ回転させますよね。(この回転させることを、写像するとか言ったりします。)
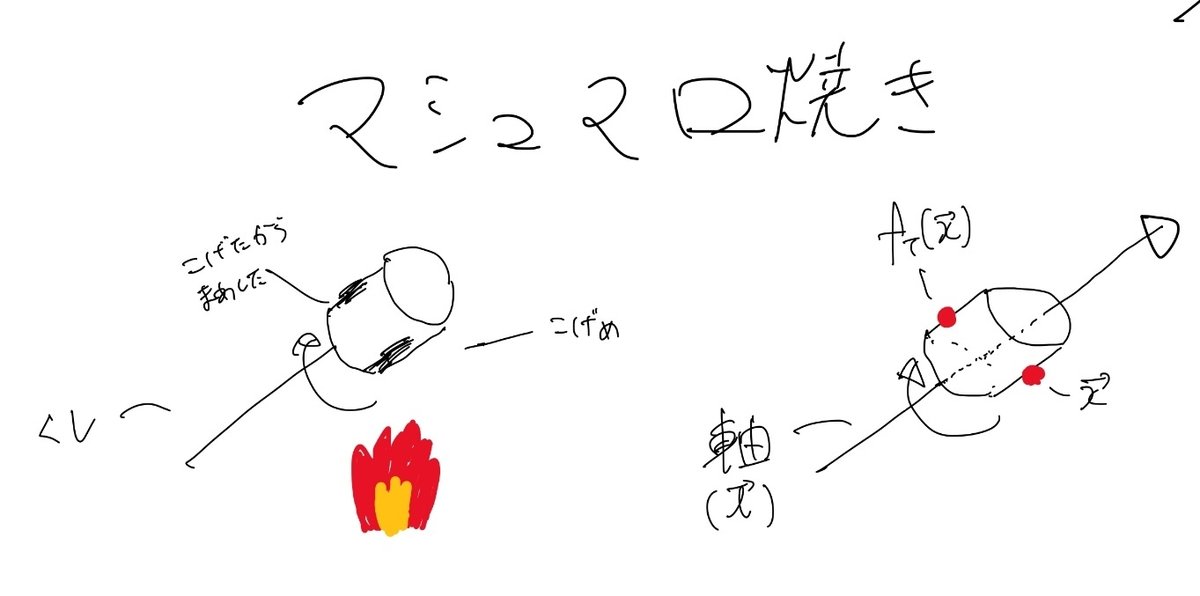
$${f_T(\vec{x})}$$の使い方をおさらいします。$${f_T(\vec{x})}$$の$${\vec{x}}$$にはいろいろなベクトルを代入してもよいです。$${(1,1,1)}$$やら$${(0,1,2)}$$やら$${(100,1000,10000)}$$やら、どれを代入しても、ある軸を中心にぐるっと回転させます。写像させているのです。

この軸を$${回転軸の方向ベクトル\vec{l}}$$と呼びます。ちなみに、どれぐらい回転するかは、$${特殊直交行列T}$$次第です。
ここまで理解出来たら、問題は解けます。
今から記述するある事さえ覚えれば、この手の問題は芋ずる式に解けます!
それは、
回転軸のベクトルは、回転前も回転後も同じ位置に存在する
ということです。
どういうことか詳しく解説します。
ここで、ベクトルを矢印と考えるとわけわかんなくなるので、ベクトルを座標の点で考えましょう。位置ベクトルというやつです。

$${\vec{l}}$$は回転軸に存在するある一点と考えることです。この場合に、軸を回転させましょう。すなわち、写像させることです。
簡単に想像つくでしょうか、回転しても全く位置は変わりません。
そのため、$${変化後=変化前}$$ということで$${f_T(\vec{\,l\,})=\vec{l}}$$と表記されます。
また、先程に$${f_T(\vec{l})=T\vec{l}}$$となることについても解説しました。
すなわち、$${f_T(\vec{l})=\vec{l}=T\vec{l}}$$が成り立つのです。
$${\vec{l}=T\vec{x}}$$について着目しましょう。対角化と似たような変形ができそうです。具体的に以下のようにします。
計算(方向ベクトル)
便宜的に、$${\vec{l}=E\vec{l}}$$と表記すると($${E}$$は単位行列)
$${E\vec{l}=T\vec{l}\Leftrightarrow T\vec{l}-E\vec{l}=\vec{0}\Leftrightarrow (T-E)\vec{l}=\vec{0}\\ここで、T-E=Aとすると、A=\dfrac{1}{3}\begin{pmatrix}-1&2&2\\2&-1&2\\2&2&-1\end{pmatrix}-\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}=\dfrac{1}{3}\begin{pmatrix}-1&2&2\\2&-1&2\\2&2&-1\end{pmatrix}-\dfrac{1}{3}\begin{pmatrix}3&0&0\\0&3&0\\0&0&3\end{pmatrix}=\dfrac{1}{3}\begin{pmatrix}-4&2&2\\2&-4&2\\2&2&-4\end{pmatrix}\\ここで、A\vec{l}=\vec{0}を解くと、A=\dfrac{2}{3}\begin{pmatrix}-2&1&1\\1&-2&1\\1&1&-2\end{pmatrix}より、簡約化して、\begin{pmatrix}2&-1&-1&\\2&-1&-1\\1&1&-2\end{pmatrix}(1行目×(-1),2行目に3行目を足す)\sim \begin{pmatrix}1&-2&1\\1&1&-2\\0&0&0\end{pmatrix}(1行目、2行目に三行目を引く、その後2,3行を入れ替える)\sim \begin{pmatrix}1&0&-1\\0&1&-1\\0&0&0\end{pmatrix}となり、\vec{l}=\begin{pmatrix}x\\y\\z\end{pmatrix}とすると、\begin{pmatrix}1&0&-1\\0&1&-1\\0&0&0\end{pmatrix} \begin{pmatrix}x\\y\\z\end{pmatrix}\Leftrightarrow x-z=0,y-z=0から\vec{l}=c\begin{pmatrix}1\\1\\1\end{pmatrix}(cは定数)\\よって方向ベクトルは\begin{pmatrix}1\\1\\1\end{pmatrix}となる.}$$
ここまでの作業は、$${f_T(\vec{l})=\vec{l}=T\vec{l}}$$から、$${(T-E)\vec{l}=\vec{0}}$$を導き、$${\vec{l}}$$の連立方程式に見立て、解を求めました。
計算(余弦)
残りの余弦を求めていきましょう!
先に言うと、内積の公式で求まります!
$${\cos\theta=\dfrac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}}$$です
一旦頭を整理します。方向ベクトルは、回転前と回転後では座標が同じなので求まりました。
ここで、余弦を考えるときは、方向ベクトルのように特定のベクトルのみを考えるのではありません。ただ単に、一般的なある点が回転したとき、何度回転したのかを問われています。
なので求めるときも、適当に任意の座標$${\vec{x}}$$を用意して変化後の$${\vec{y}(=f_T{\vec{x})}$$の座標を求めてから内積すればよいのです!
$${\vec{x}}$$を用意します。ここで、特殊直交行列の名前の伏線回収がされるのですが、任意のベクトル$${\vec{x}}$$は方向ベクトル$${\vec{l}}$$に垂直に交わります。

なので、直交という名前なのです。要は$${\vec{x}・\vec{l}=0}$$です。$${\vec{l}}$$=(1,1,1)と内積が0になるようにしましょう。
そうなるように$${\vec{x}}$$を作ってください。例えば、(1,0,-1)や(3,-1,-2)や(5,-7,2)など、なんでもよいです。(便宜上横ベクトル表記にしました。本当は縦です。)
$${\vec{x}=\begin{pmatrix}1\\0\\-1\end{pmatrix}}$$にします。
すると、$${f_T(\vec{x})=T\vec{x}=\dfrac{1}{3}\begin{pmatrix}-1&2&2\\2&-1&2\\2&2&-1\end{pmatrix}\begin{pmatrix}1\\0\\-1\end{pmatrix}=・・・=\begin{pmatrix}-1\\0\\1\end{pmatrix}}$$
となります!あとは内積を取ると
$${\cos\theta=\dfrac{\vec{x}・f_T(\vec{x})}{|\vec{x}||f_T(\vec{x})|}=\dfrac{-1+0-1}{\sqrt{2}・\sqrt{2}}=-1}$$ となって終了です!
後半をまとめると、任意の$${\vec{x}}$$を定め、$${f_T(\vec{x})}$$を求めてから内積で余弦を求めていきます!
最後までお読みいただきありがとうございました。読者の皆様に、少しでもお役立ちいただけたら幸いです。
この記事が気に入ったらサポートをしてみませんか?
