3Dゲームにおける内積・外積・四元数について
内積・外積・四元数を使う必要性
2Dゲームでは主に三角関数をメインで使うことが多かったと思う。
しかしこと3D空間においてはそうはいかない場面が多い。
なぜなら角度を求めたとしてどの軸の角度なのかや、最短でプレイヤーの方向を向くとなるとあまりきれいなコードは書きにくい。
そうなると作るゲームの自由度が下がってしまうことにつながる。
そのためこの3つを上手く扱うことで処理負荷を減らしたり新しい表現を身に着けることができるのだ。
内積について
そもそも内積とはベクトル同士の掛け算の仕方の一種である。
3Dゲームでは主に正規化したベクトル同士の角度を求めるときに使う。
内積のイメージと公式
正規化したベクトル同士($${\vec{a}}$$, $${\vec{b}}$$)を内積すると$${\vec{a}}$$から$${\vec{b}}$$に掛けて垂線を下し、原点から垂線にかけての長さを求めるイメージを持ってほしい。

では$${c}$$はどのような公式で求めることができるのだろうか。
実は内積は複数種類の公式があるがゲームで主に使う公式は以下の式だ。
$${c = \vec{a}.x × \vec{b}.x + \vec{a}.y × \vec{b}.y}$$
注意してほしいのはこのとき$${\underline{求めたcはベクトルではなくただの実数になるという点だ。}}$$
実際に計算してみるとわかるのだが正規化したベクトル同士の内積は
-1~+1の間に収まる。
このままでは何に使うかイメージしにくいと思うので使いやすい形に変えてみよう。
内積の値を角度に変換
内積で求めた値(-1~+1)はベクトル間の角度を求めることができる。
ベクトル間の角度というのは以下の部分のことだ。

結論から言うと内積の値は逆三角関数の1つである$${\arccos}$$に入れることで角度に変換できるのだ。
この性質を利用することで敵が視野角内にいるかどうかなどのプログラムを書くことができるぞ!
外積について
外積もベクトル同士の掛け算の仕方の一種類である。
3Dゲームでは主に一方のベクトルから見てもう片方がどちら側を向いているかを求めるときに使う。
外積のイメージと公式
正規化したベクトル同士($${\vec{a}}$$, $${\vec{b}}$$)を外積すると$${\vec{a}}$$と$${\vec{b}}$$に対して垂直なベクトル$${\vec{c}}$$を求めることができる。
以下のイメージ図は右手座標系をもとに再現している。

では$${\vec{c}}$$はどのような公式で求めることができるのだろうか。
外積は以下の式で求めることができる。
$${\vec{c}.x = \vec{a}.y × \vec{b}.z - \vec{a}.z × \vec{b}.y}$$
$${\vec{c}.y = \vec{a}.z × \vec{b}.x - \vec{a}.x × \vec{b}.z}$$
$${\vec{c}.z = \vec{a}.x × \vec{b}.y - \vec{a}.y × \vec{b}.x}$$
ちなみに公式を眺めていればわかることなのだが
$${\underline{かける順番を入れ替えると求まるベクトルが反転することに注意がいる。}}$$
ではベクトルが求まったから何になるのだという話をしていこうと思う。
外積のベクトルで向きを判断
今回は$${\vec{a}}$$と$${\vec{b}}$$がそれぞれ$${y}$$の値が0であると想定して話を進めていく。
まずは$${\vec{a} = [0, 0, 1]}$$と$${\vec{b} = [1, 0, 0]}$$で外積をとるとどのようになるだろうか。
途中式はめんどくさいので省くが$${\vec{c} = [0, 1, 0]}$$というベクトルを求めることができる。

では次に$${\vec{a} = [0, 0, 1]}$$はそのままに$${\vec{b} = [-1, 0, 0]}$$で外積をとるとどのようになるだろうか。
これも途中式はめんどくさいので省くがこんどは$${\vec{c} = [0, -1, 0]}$$というベクトルを求めることができた。
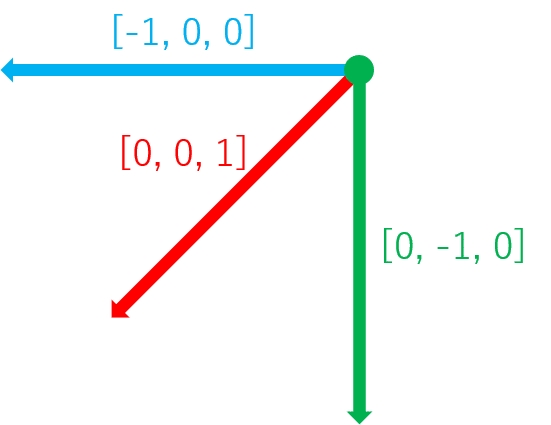
$${\vec{a}}$$を視線ベクトルとするとそこから見て左向きのベクトルが出ているなら$${\vec{c}.y}$$の値が0以上になるし、右向きのベクトルが出ているなら$${\vec{c}.y}$$の値が0以下になることがわかる。
この性質を利用することで敵がどちら側にいるかなどの向きを取得することができるのだ。
四元数(クォータニオン)
四元数とは複素数を拡張したものであるが、
こと3Dゲームでは主に回転を表現するときに用いるものだ。
四元数のイメージ
とりあえず難しいことは考えずに3Dゲームにおける四元数のイメージをつかんでほしい。
軸ベクトルを刺してその軸をもとにθだけ回転させる
というものだ。
この時の軸ベクトルは正規化されたものとする。

公式自体は結構複雑なので各々調べてほしい。
しかし、このイメージをもって使うことで回転表現が大幅に増えることは間違いないだろう。
四元数のメリット
実は回転を表現する方法としてヨーピッチロールで表される回転行列を用いる方法も存在している。
四元数に変えることでどのようなメリットがあるのかを考えていこう。
ジンバルロックが起こらない
ジンバルロックとは何かについて説明しよう。
簡単に言うならば回転しなくなるバグのことである。
回転を表現しているものは基本的に掛け算を行うことでどんどん回転を加えることが可能なのだが、ことヨーピッチロールの回転行列ではある一定の条件下に陥ると以降どんなに回転を掛け算しても回転しなくなる事象がおきる。これをジンバルロックというが四元数ではそれが起きないのだ。
計算処理が低コスト
ヨーピッチロールの回転行列ではZ軸回転とY軸回転とX軸回転のそれぞれの行列をかけ合わせることで表現していた。
しかし四元数はそれ1つでその3要素を合わせた回転行列を生み出すことができるので余分な行列の掛け算が発生しなくなり処理が軽くなるのだ。
こういった事象を考えるとほぼ回転は四元数一択といっても差し支えないだろう。
四元数の扱い方の一例
四元数で回転を表現する際は軸と角度が必要であった。
ここで察しの良い人はもうすでに気づいているのかもしれない。
そう、外積と内積を組み合わせられそうというイメージを持ってほしい。
外積で軸を求めて、内積で角度を割り出す。
そうすることでキャラクター制御の幅がうんと広がることだろう。
例えばプレイヤー制御において移動したい方向に体を向ける処理なんかも
移動方向のベクトルと現在の向きベクトルの2つあれば回転の補完なども行うことができるのだ。
実際の実装については各々やってみて欲しい。
この記事が気に入ったらサポートをしてみませんか?
