2024年5月15日 雑記「世間のエーアイ騒ぎを見て」
最近、Twitterでは常に「生成AI」が燃えている。生成AI利用に関わる問題点を考えると燃えることもあるだろう、という状況ではあるが、トレンドの「生成AI」をクリックして流れてくるようなツイートの多くがそもそも言葉の定義を全然わかっていないことにかなり嫌悪感を覚えた。僕はかつて数学を専攻していた、ということはいつかの記事で書いたはずだ。だから「定義」というものの大切さを平均的な人よりもずっとよく知っていて、それが雑に扱われることがどうしても腹立たしく思えてしまう。定義の不明瞭な概念に対して大勢の人が怒っている、ということがここまでの規模で発生するのもそう頻発するものでもないだろう。自分が何に対して怒っているのか、ということを正確に理解しないまま感情を爆発させるというのは不幸なことだと思う。というのも、その怒りはおそらく「別の誰かの怒り」だからだ。誰かに怒らされるのではなく、怒りの対象を明確にし、自分自身の心からの反抗心により魂を燃やして怒ること、それこそが真に美しく、尊重されるべき、意味のある怒りではないだろうか。
「AI(人工知能)」は大規模データの統計的機械学習によって入力と出力が対応づけられたモデルであると考えられがちだが、そうではない。ヒトのふるまいをシミュレートするのはなにも統計的な操作だけが実現できる特権ではなく、ごくシンプルなものであれば「"おはよう"と言われたら"おはよう"と返す」のようなルールを与えることで統計学とは関係のないところで実現できる。しかし、昨今「AI」という言葉が使われる際はほとんどの場合「統計的機械学習」によるものを指す。そのため、(まことに残念ながら)「AI」の説明をするためには「統計的機械学習」に絞って話す必要がある。
「学習」とは何だろう? 人間の場合は「経験によって生じる比較的永続的な行動の変化、それを生じさせる操作、およびその過程」であると定義されている。我々は学習によって「道で溝にはまって以降そこを通らないようにする」「問題集を解いてパターンを把握し、様々な問題に対し正しい解答を書けるようにする」などといったことができるようになる。
AIの場合も似たような「学習」を行う。ここで説明するのは「生成AI」ではなくもっとシンプルな「正解が決まっているものの正解を当てようとするAI」だが、生成AIでも何をモデル化するか(p(y|x) か p(x, y) か)が違うだけで「何をしていないか」については同様であると思ってもらって差し支えない。
学習をするにはまず「仮説」の導入が必要となる。例えば体重 y と身長 x の関係がなんらかのパラメータ a, b を用いて y = ax + b という式で表せるとする。本当にそうなっているかはわからないが、ともかくそうであると「あたり」をつけておく。試しに y = 0.6 x - 40 などとしてやれば、あなたの体重とそう大きく違わない数値が出るかもしれない。実際には個体差があるので、体重と身長は誤差 e を含んだ y = 0.6 x - 40 + e というふうな関係で表すのが適切と思われる。a と b がどんな値であるかは、体重と身長のデータを用いてなんらかの方法で推定できる。
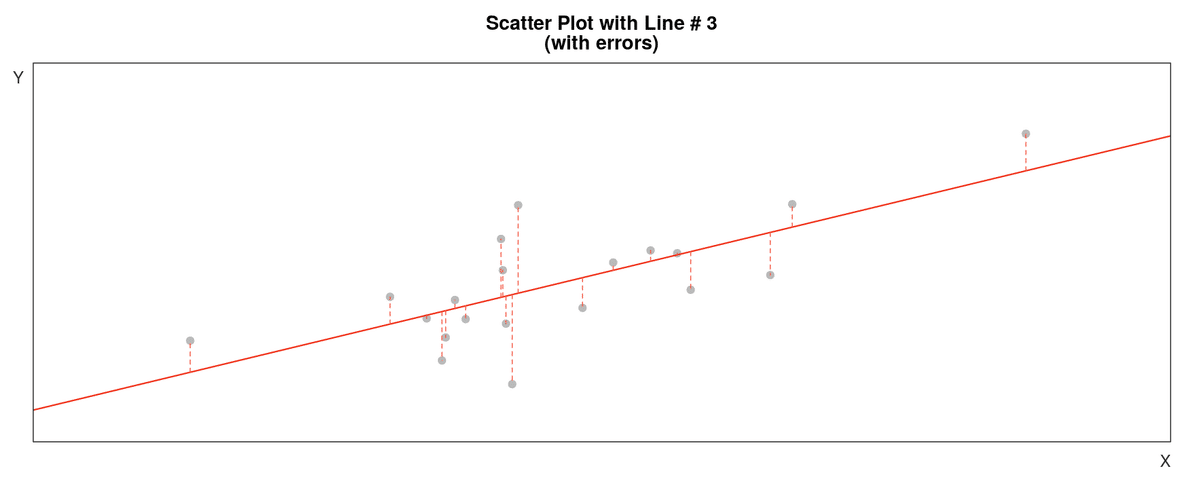
よく使われるのは「最小二乗法」だ。以下の画像がイメージしやすい。灰色の点がデータ(縦軸が体重、横軸が身長)で、体重と身長の関係をうまく表してくれるような赤い直線(y = ax + b)を引きたい。しかし、誤差 e があるため「すべての点を綺麗に通るような直線」はなかなか引くことができない。そこで適切な直線を「なるべくデータとの距離が小さくなるような直線」と考える。具体的には、実際のデータ d と y = ax + b との差 d - y を(計算の都合上、2乗して)足し合わせた Σ (d - y)² が最も小さくなるような a, b を採用する。そのような a, b は微分によって手計算で求めたり、コンピュータを用いて簡単に求めたりできる。
AIにおける「学習」とは、「仮説たち」(ここでは y = ax + b)の中から適切な「仮説」(ここでは y = 0.6x - 40)を選び出すことを意味する。この「仮説たち」がめちゃくちゃ複雑でパラメータの数がとんでもなく多いのが、最近騒がれているようなAIだ。よく「AIがやっているのは元データの切り貼りや引用である」と言われるが、少なくともこの主張は正しくない。公開されている個々の「モデル」は
画像 y と言葉 x が y = f(x) という関係で表せると仮定する
大量の y と x の組(「りんごの画像」と「りんご」という言葉、「バナナの画像」と「バナナ」という言葉など)から、適切な仮説 f を選び出す
という手順を経た f のことであり、元のデータは持っていない。持っているのは「仮説」を特定するためのパラメータだ。「モデルを解析したら元画像が見つかった」という与太話もこの理由から即座におかしいと判断できる。そのため、「切り貼り」「引用」「圧縮」という言葉で表されるような操作は入り込む余地がなく、こういう表現は理工系の人にはどうしても「トンデモ」に聞こえてしまう。いくら切実に問題を訴えても、この時点で「野生の相対性理論間違い指摘おじさんが突っ込んできた」ように見えて第一印象が完全に破滅する、という状況がステークホルダー同士の対話を難しくしている。実際、僕はこういうのを見て毎日とんでもなく不快な気分になっている。
ここでややこしい点がふたつある。ひとつは、最近流行りの「Diffusionモデル」の学習方法が上記の直線モデルとは少し違うことだ。Diffusionモデルでは、元データにノイズを加えていき最終的にガウシアンノイズになるまでの過程を用いて逆に「ノイズ除去のしかた」を学習する。これも「元データそのものを保持してはいない」という点で同じだが、単純に誤差を小さくしていくだけの学習よりも元データと似通った出力を得ることがより容易になっている。もうひとつは、最近のモデルがとんでもない数のパラメータを持っているということだ。一定以上の表現力を持つ「仮説」からは、元のデータを持っていなくともとても似たものが得られてしまう、ということが発生し、あたかも「元データの切り貼り」に見えてしまうかもしれない。けれども、その問題点を正しく指摘するには「なぜそう見えるのか」を正しく把握する必要がある。以下の記事で指摘されているように、それができないのであれば「内部動作に踏み込まずに出力結果について議論」するほかない。
確かに倫理的に問題のあるような使い方をするユーザーはいるし、それによって実害も多く発生するだろう。しかし、どんな切実な問題であろうと、端的に間違ったことに基づいて何かが議論されるということはそれらとは比べ物にならないほど恐ろしい。いかに酷い目に遭った被害者であろうと、事実に反した批判に加担してしまった時点でそこに正義はなくなってしまう。正しく問題点を切り分け、正しく批判する、多くの人がこれを心がけるようになってほしい。こういうことを言うと、いくら丁寧に説明しても「お前は〇〇側の味方なのか」と突っかかってくるやつが必ず出てくるが、強いて言うならば僕はその立場に関係なく「事実に基づいて議論する側」の味方をしていたい。
この記事が気に入ったらサポートをしてみませんか?
