Proof of the infinite existence of twin primes based on the ratio of primes and composite numbers (Preprint)
Abstract:
This paper offers a proof of the infinite existence of twin prime numbers, a unique category of primes. It combines empirical data with the Prime Number Theorem to elucidate the growth of twin primes. The analysis, spanning pair tables from 1 to 10⁸, demonstrates the existence of prime pairs when certain conditions are met. Extending the analysis to pair tables from 10⁹ using the Prime Number Theorem, it suggests that twin primes continue to increase with positive integers. This proof contributes to resolving the longstanding mathematical problem of the existence of infinitely many twin primes.
Introduction:
Twin prime numbers are a unique category of primes. Typically, prime numbers, excluding 2 and 3, can be found in pairs within an arithmetic sequence with an initial term of 1, starting from the zeroth term, and a common difference of 6.

In Table 1, numbers with a blue background represent composite numbers, while those with a red background are prime numbers. By categorizing the number of primes and composites for each value of n in Table 1, we can classify them into four patterns:
24 Patterns: 2 composite numbers, 4 prime numbers.
42 Patterns: 4 composite numbers, 2 prime numbers.
51 Patterns: 5 composite numbers, 1 prime number.
60 Patterns: 6 composite numbers, 0 prime numbers.
Twin prime numbers, the focus of this study, correspond to the 24 and 42 patterns, where there is one composite number between two prime numbers. The question of whether these pairs exist infinitely is an unsolved problem.
It's worth noting that consecutive prime numbers like 3, 5, and 7 (three in a row) are distinct from twin primes. Prime numbers, except for 2 and 3, are found in the sequences xₙ and xₙ-2 of an arithmetic progression, so having only one such pair is expected.
Trends in Prime Number Distribution:
Figure 1 depicts the distribution of prime numbers. The X-axis represents n, ranging up to n = 1000 in the sequence xₙ, while the Y-axis displays various data related to prime and composite numbers. Specifically, it shows:
The actual count of prime numbers (f: thin red line).
The count of composite numbers (g: thin blue line).
The count of prime numbers based on the Prime Number Theorem (c: thick red line, serving as a reference akin to an average based on real numbers).
The count of composite numbers (d: thick blue line).
The graph on the right side presents a logarithmic scale on the X-axis.
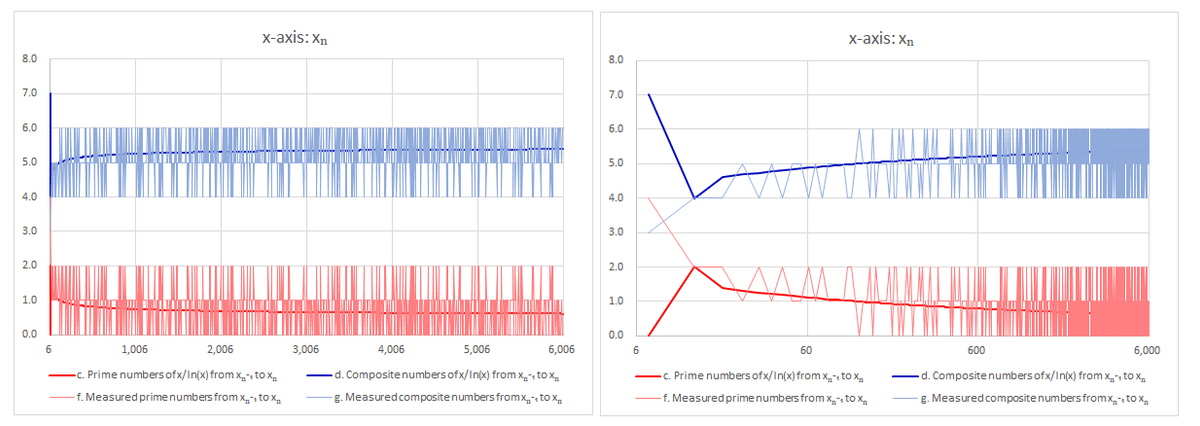
The distribution starts with 24 patterns and continues up to 60 patterns.
Between these ranges, the patterns 42 and 51 are repeated cyclically.
After reaching patterns 60, the sequence returns to patterns 42, 51, and 60.
In terms of patterns, the prime and composite numbers exhibit symmetry, mirroring each other around a multiple of 3, as prime numbers, excluding 2 and 3, often appear in pairs around composite numbers in the sequence. This leads to a recurring pattern where composite numbers occur in sets of 4, 5, or 6, and prime numbers follow a similar pattern with 2, 1, or 0 primes in between. However, since the count of composite numbers, a measure akin to an average from the Prime Number Theorem (d), exceeds 5, there is the possibility that the pattern may involve repeating 5 and 6, and consequently, prime numbers repeating 1 and 0. This pattern's behavior as n approaches infinity, specifically whether the patterns 42 continue indefinitely, remains an unsolved problem. However, due to computational limitations, the study seeks to explore what can be inferred by incorporating the Prime Number Theorem.
Analyzing Pair Numbers from the Ratio of Primes and Composite Numbers in Empirical Data:
Let's examine the number of pair tables (referred to as "n") from 1 to 10⁸, which can be easily calculated on a computer. In each pair table, there are "a" odd numbers, where "a" is equal to 2 times "n" (since each pair table has 2 seats). We have "b" prime numbers excluding 2 and 3 in empirical data, and the number of composite numbers is "c" (the ratio of composite numbers to odd numbers is "d," where d = c / 2a). Since the prime number range is from xₙ - 2 to xₙ, which is half of xₙ - 5 to xₙ, the upper limit number when all numbers become pairs by becoming composite numbers is "e" (the ratio is "f," where f = e / c). The lower limit pair number of composite numbers when all prime numbers become pairs with composite numbers (in other words, prime numbers that are not paired with composite numbers are paired with each other) is "g" (the ratio is "h," where h = g / c). Table 2 shows that for any "n," h < d < f, but when d exceeds h, it explains the existence of prime pairs.
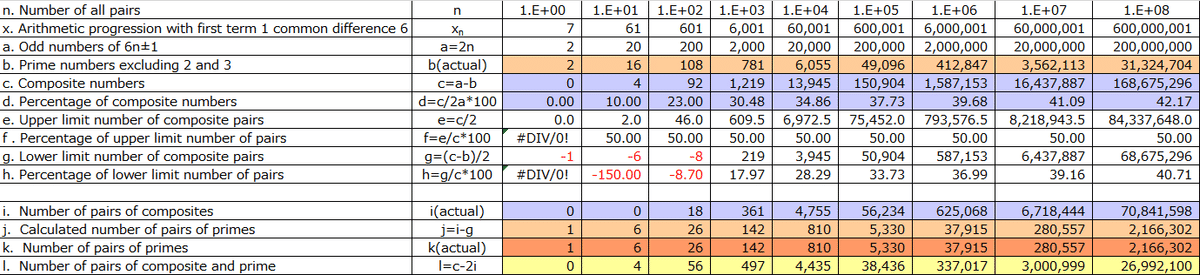
We can obtain the number of pairings between composite numbers empirically as "i," and the number of pairings between prime numbers empirically as "j" = "i" - "g" (for example, if there are 10 pair tables, 16 prime numbers, and 4 composite numbers, with no pairings between composite numbers, it is necessary for prime pairs to exist in 6 pair tables, and it is inevitable that mixed pairs of prime numbers and composite numbers exist in 4 pair tables). Let's check with the empirically obtained number of pairings between prime numbers, "j." Surprisingly, "i" = "j" is a complete match. Additionally, the number of mixed pairs of prime numbers and composite numbers can be calculated as "l" = "c" - 2"j". The mixed pair ratio peaks at 10² but remains higher than the composite pair ratio up to 10³, after which the composite pair ratio surpasses it.
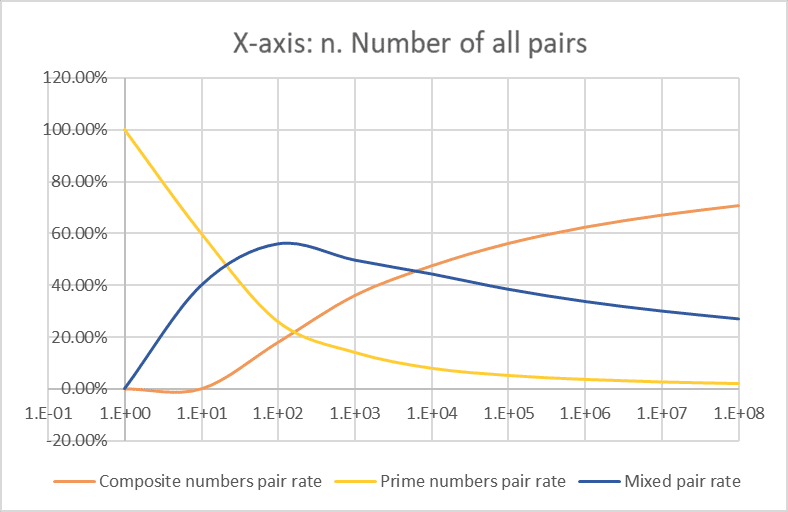
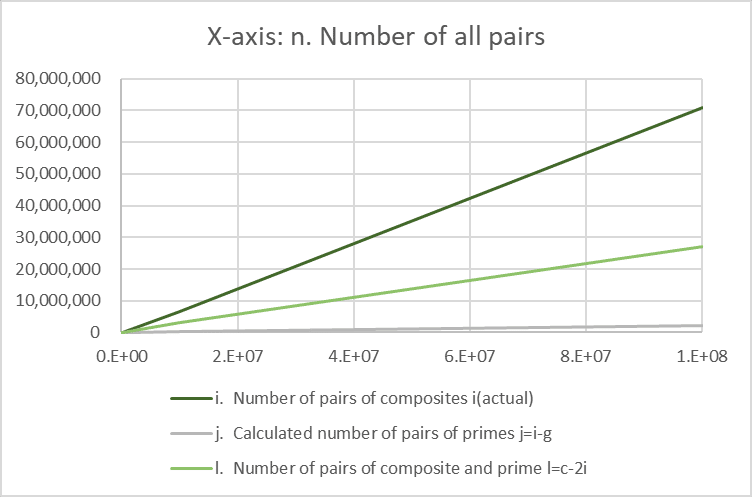
Based on the above analysis, it is demonstrated that the difference between "i" and "g" represents the number of prime pairs. Thus, for the number of pair tables "n" from 1 to 10⁸, it has been explained that when "d" exceeds "h," prime pairs exist.
Analyzing Pair Numbers Based on the Prime Number Theorem:
When considering the number of pair tables ("n") starting from 10⁹ and using the Prime Number Theorem, we can directly warp to the formula. We replace the number of prime numbers excluding 2 and 3 in Table 2 with "b" = x / ln(x) - 2, and we check whether "d" exceeds "h."

However, the calculation reached its computational limit at 10⁵⁰⁰. Although the validity of calculations from 10¹⁶ to 10¹⁰⁰ is questionable due to insufficient significant figures, there is still a difference between "d" and "h." Even with a difference as small as 10⁰⁰, it seems that "d" continues to surpass "h," maintaining the ranking of ratios seen in Figure 2 (Figure 4).
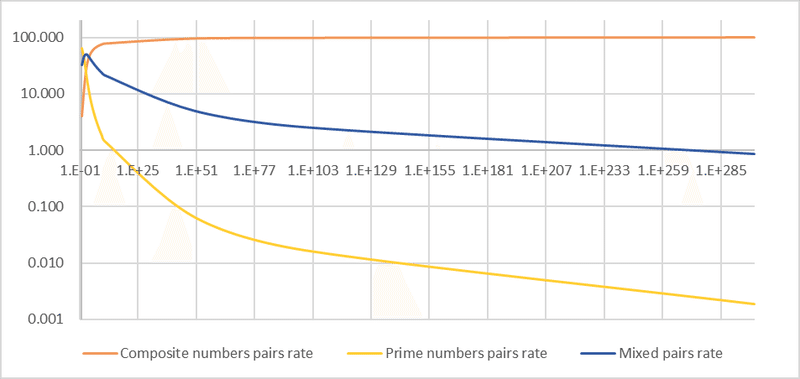
While it might appear that the ratios will no longer change significantly, when considering the number of pairs, twin primes continue to increase proportionally with "n."
In summary, when comparing directly using the formula:
d : h ⇒ c/2a : g/c ⇒ c/2a : (c-b)/2c ⇒ c/a : (c-b)/c ⇒ c² : a(c-b) ⇒ c² : (c+b)(c-b) ⇒ c² > c² - b²
This inequality relationship suggests that twin primes continue to grow with "n."
Conclusion:
The main proof point of this paper is the demonstration of the existence of twin primes increasing proportionally with positive integers. This growth relationship has been confirmed through empirical data and the Prime Number Theorem, providing evidence for the infinite existence of twin primes.
The proof of this growth relationship represents a mathematically significant result, offering new insights into the long-standing unsolved problem of the existence of infinitely many twin primes. While the accuracy of this proof should undergo thorough verification within the mathematical community, its confirmation would mark the resolution of a significant problem in mathematics.
It's worth noting that this proof employs a methodology similar to the one used for the Goldbach Conjecture. However, the presence of either prime or composite numbers in pairs at xₙ−₂ and xₙ makes the case of twin primes clearer and reinforces the proof of the Goldbach Conjecture.
Acknowledgments:
I would like to express my gratitude to those who engaged in discussions and provided valuable insights on web forums during this solitary research journey. Additionally, I extend my appreciation to ChatGPT for its assistance throughout the process. Your contributions and support have been instrumental in the progress of this research.
References:
Request for a Letter of Recommendation for Submission to a Peer-Reviewed Journal:
To support the submission of this significant contribution, I kindly request a letter of recommendation from a qualified mathematician with expertise in the relevant field. The letter should be signed and written on official letterhead, confirming their understanding of the arguments presented in this paper and attesting to its correctness.
Please note that physical letters, not electronic, are required for submission and should be sent by regular mail. Thank you.
この記事が気に入ったらサポートをしてみませんか?
