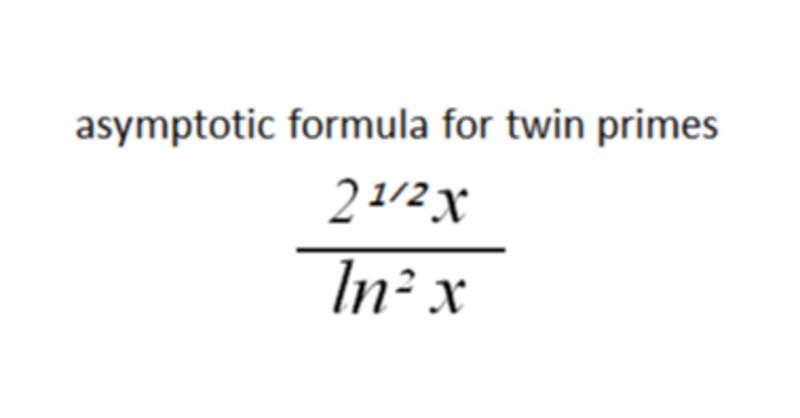
The Ratio of Prime and Composite Numbers Proves the Infinity of Twin Primes (Preprint)
Abstract:
This research provides new insights into prime numbers and twin primes. It suggests that the function x/ln(x) is more powerful than π(x) (the count of prime numbers less than or equal to x) in addressing problems related to prime number distribution. Specifically, an approach based on the ratio of composite numbers to odd integers was examined, revealing that x/ln(x) signifies the infinite existence of twin primes. Furthermore, it was established that the asymptotic formula for twin primes is 2¹ᐟ²x/(ln x)². This study yields mathematically significant results and enhances our understanding of the long-standing question of the infinitude of twin primes. The accuracy of this proof awaits verification by the mathematical community, and its confirmation would mark a significant milestone in mathematics.
Introduction:
In general, prime numbers, excluding 2 and 3, are found in the arithmetic sequence with a common difference of 6, starting with 1 as the 0th term, denoted as xₙ and xₙ-2 (for n ≥ 1).

In Table 1, numbers with a blue background are composite, while numbers with a red background are prime.
When we categorize the number of primes and composites for each n in Table 1, we can classify them into four patterns:
24 patterns... 2 composite numbers, 4 prime numbers,
42 patterns... 4 composite numbers, 2 prime numbers,
51 patterns... 5 composite numbers, 1 prime number,
60 patterns... 6 composite numbers, 0 prime numbers.
Twin primes refer to pairs of prime numbers that fall in the 24 and 42 patterns, with one composite number between them. The question of whether such pairs exist infinitely is an unresolved problem [1].
Figure 1 displays the distribution of xₙ, where the X-axis ranges up to n = 1000, and the Y-axis represents the actual count of prime numbers (f: thin red line), composite numbers (g: thin blue line), prime numbers according to the prime number theorem [2] (c: thick red line, serving as an indicator resembling real-numbered averages), and composite numbers (d: thick blue line). The right side of the graph uses a logarithmic scale on the X-axis.
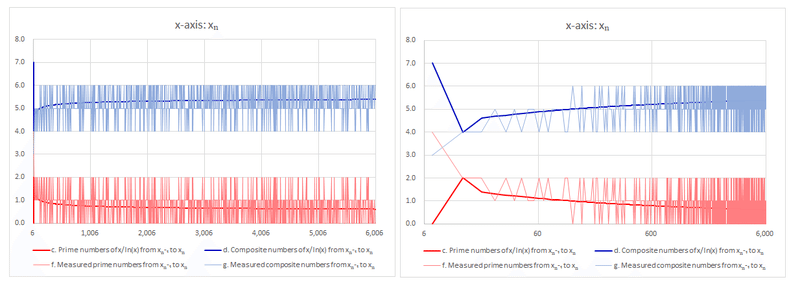
The observed trends begin with 24 patterns and continue repeating through 42 and 51 patterns until reaching 60. Regardless of the specific pattern, the distribution of prime numbers exhibits symmetry around 3 (prime numbers, except for 2 and 3, are positioned around multiples of 3 in the sequence).
Consequently, if composite numbers repeat as 4, 5, 6, prime numbers will repeat as 2, 1, 0, respectively. However, since the indicator for composite numbers (d), which serves as an average-like measure according to the prime number theorem, exceeds 5, there is also a possibility of prime numbers repeating as 5, 6, and composite numbers repeating as 1, 0. This leads to an unsolved problem: whether the 42 patterns will continue to increase as n approaches infinity. Nevertheless, due to practical limitations in measurements, we explore what can be inferred by incorporating the prime number theorem.
Analysis of Pair Counts Based on the Ratio of Prime and Composite Numbers in Empirical Measurements:
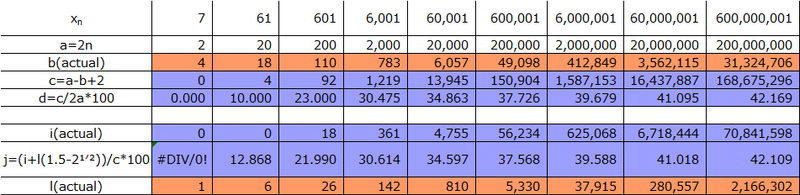
We will examine the number of pairs for various values of n, ranging from 1 to 10^8 (a computationally manageable range). In this analysis, we consider the number of odd integers in an arithmetic sequence xₙ with a common difference of 2n (assuming two seats per pair table), the actual count of prime numbers (b, excluding 2 and 3), and the count of composite numbers (c = 2n - b). The ratio of composite numbers to odd integers is denoted as d = c / 2n.
As the prime number domain from xₙ-2 to xₙ constitutes half of the domain from xₙ-5 to xₙ, we have e = c / 2 as the upper limit count when all composite numbers form pairs. The ratio of this count, f = e / c, is calculated. Likewise, for the scenario where all prime numbers form pairs with composite numbers (meaning the remaining prime numbers do not form pairs with each other),
we determine the lower limit count of pairs formed by composite numbers, g = (c - b) / 2, and the ratio of this count h = g / c, is calculated.
Table 2 summarizes the observations, showing that for all values of n, h < d < f. When d surpasses h, it implies the existence of pairs formed by prime numbers.
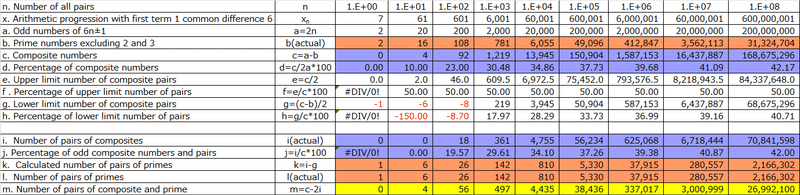
The count of pairs formed by composite numbers in empirical measurements is denoted as i, and the count of pairs formed by prime numbers can be determined as k = i - g. For instance, if there are 10 tables (n = 10) with 16 prime numbers and 4 composite numbers, and if the count of pairs formed by composite numbers is 0, then there must be 6 tables where prime numbers pair with each other, and 4 tables with a mix of prime and composite pairs.
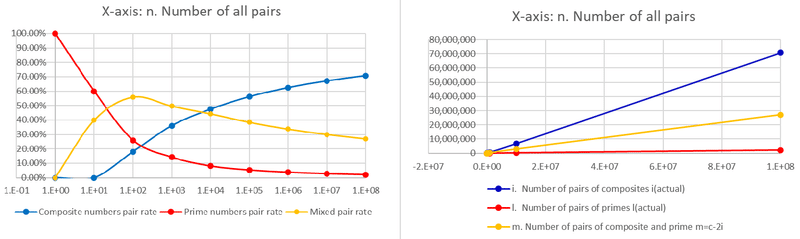
Let's cross-check this with the count of pairs formed by prime numbers, denoted as l. Surprisingly, k = l, indicating a perfect match. Additionally, the count of mixed pairs, where prime and composite numbers coexist, can be determined as m = c - 2i. The rate of mixed pairs peaks at 10^2 and is higher than that of pairs formed by composite numbers until 10^3. However, beyond 10^4, the rate of pairs formed by composite numbers exceeds that of mixed pairs.
Based on the above analysis, the difference between i and g has been established as the count of pairs formed by prime numbers. This proves that when the number of table pairs n is between 1 and 10^8, if d surpasses h, there exist pairs formed by prime numbers. By directly comparing the formulas:
d : h ⇒ c/2n : g/c ⇒ c/2n : (c-b)/2c ⇒ c/a : (c-b)/c ⇒ c² : a(c-b)
⇒ c² : (c+b)(c-b) ⇒ c² : c²-b²
We have confirmed that d > h based on this inequality.
Understanding the ratio of prime and composite numbers and the count of pairs formed by composite numbers opens the door to exploring the regularity of the ratio for accurately determining the count of pairs formed by prime numbers using the prime number theorem.
Prime Number Theorem and Estimating Pair Counts:
The number of tables (n) for pair seating ranges from 10⁹ to the computational limit. To simplify empirical measurements, we substitute the actual count of prime numbers (b = x/ln(x), where ln denotes the natural logarithm) and approximate the count of pair pairs between composite numbers (i = cd/100).
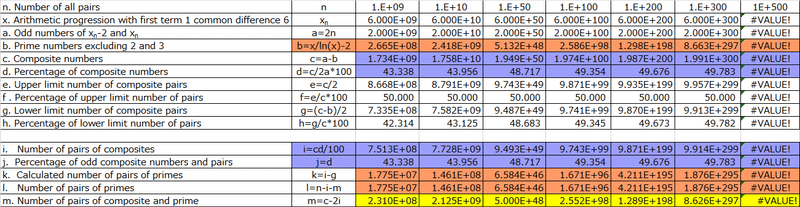
In the table, we observe that the difference between d and h (d : h) remains consistent as we divide the range of x into xₙ - xₙ₋₁ segments (Table 4). This relationship implies that, based on the prime number theorem, twin primes continue to increase infinitely.
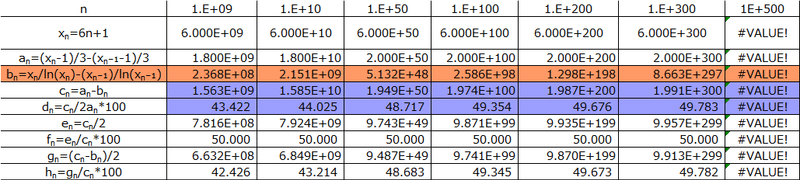
However, the calculations reach their computational limits at 10⁵⁰⁰. Although strict precision is challenging between 10¹⁶ and 10¹⁰⁰, the difference between d and h still exists, even when it becomes as narrow as one hair's breadth at 10³⁰⁰ (0.001%?). This suggests that the order of the ratios in Figure 2 remains the same, with d surpassing h (Figure 3).
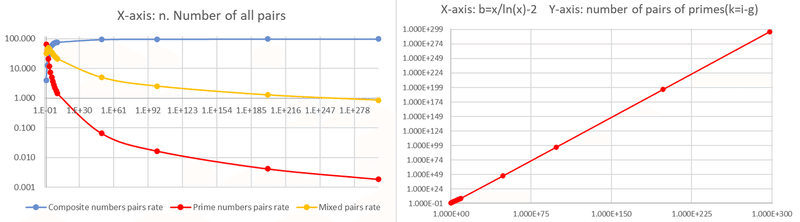
While it may seem that ratios are no longer appearing, when examining the pair counts, we find that even with this, twin primes are increasing in accordance with x/ln(x) from the prime number theorem, as seen in the asymptotic behavior of prime number distribution [3].
The asymptotic formula for twin primes, derived from the prime number theorem as x → ∞, is approximately 1.5x/(ln(x))².


Evaluation of the Asymptotic Formula for Twin Primes:
With all the necessary tools in place, we proceeded to compare the asymptotic formula for twin primes (1.5x/ln²x) with empirical data in Table 5.

The formula 1.5x/ln²x did not provide a good match (Table 6). We revisited the portion in Table 3 where we approximated 'the number of pairs of composite numbers by empirical data (i = cd/100)':
(Composite number count) / (Odd number count) ~ (Pairs of composite numbers) / (Composite number count).
This approximation was used because measuring the pairs of composite numbers empirically was quite challenging. This raises the question of whether our approximation was correct when compared to Table 5. So, we modified the 1.5 in 1.5x/(ln²x) (where 1.3 is close to the Hardy-Littlewood constant [4]) and compared it further. We found that 2¹ᐟ²x/(ln²x) provided the best asymptotic match, as shown in Figure 4.
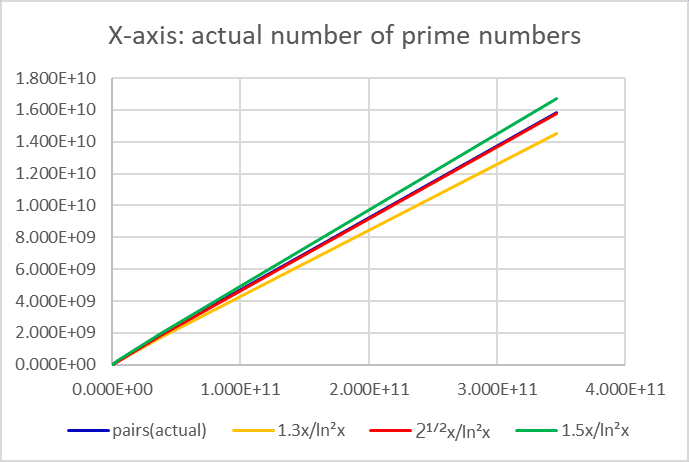
One might wonder if this is incorrect, but after careful consideration, we realized that the match in Table 3 actually validates the accuracy of 2¹ᐟ²x/(ln x)².
As we transitioned from a proportionality constant of 1.5 to 1.5-2¹ᐟ² with respect to x/ln(x), we noticed that the ratio of composite number pairs to composite numbers converges to 50% at the limit [5]. Conversely, this implies that the ratio of primes approaches 0 at the limit, which is consistent with the increasing function of the prime number theorem's x/ln(x).
Conclusion:
The main conclusion of this research suggests that the approach using the function x/ln(x) is more powerful than π(x) (the count of prime numbers less than or equal to x) in mathematical problems related to prime numbers.
Using a proof by contradiction, it was shown that in dividing the range of x, for each subrange (from xₙ to xₙ₋₁), there could exist a ratio between the count of composite numbers (x - π(x), the difference between the count of prime numbers less than or equal to x and π(x)) and the count of odd numbers (in pairs of two) that matches the ratio of lower bound pairs of composite numbers (the difference between the count of composite numbers and the count of prime numbers divided by 2 times the count of composite numbers). This potential ratio could have implications for twin primes and the Goldbach conjecture, among others. However, the approach using x/ln(x) revealed that such a ratio does not exist, leading to a contradiction.
As a result, the approach utilizing x/ln(x) was found to be a more powerful method for understanding the properties of prime numbers and solving related problems. It successfully demonstrated the infinite existence of twin primes, as expected. Furthermore, the asymptotic formula for twin primes was determined to be 2¹ᐟ²x/(ln x)², and it was shown to align with the distribution of prime numbers.
This research has brought forth mathematically significant results and provides new insights into the long-standing question of the infinitude of twin primes. The accuracy of this proof should be verified by the mathematical community, and the confirmation of the existence of twin primes will mark the resolution of one of the significant challenges in mathematics.
Acknowledgments:
I would like to express my gratitude to those who engaged in discussions and provided valuable insights on web forums during this solitary research journey. Additionally, I extend my appreciation to ChatGPT for its assistance throughout the process. Your contributions and support have been instrumental in the progress of this research.
References:
[1] Twin prime. Wikipedia. https://en.wikipedia.org/wiki/Twin_prime. Accessed September 20, 2023 UTC.
[2] Prime number theorem. Wikipedia. https://en.wikipedia.org/wiki/Prime_number_theorem. Accessed September 20, 2023 UTC.
[3] Analytic number theory. Wikipedia. https://en.wikipedia.org/wiki/Analytic_number_theory. Accessed September 20, 2023 UTC.
[4] Author(s): Goldston, D. A.; Pintz, J.; Yıldırım, C. Y. Title: Primes in Tuples I Published in: arXiv:math/0405509 [math.NT] Accessed: September 20, 2023 UTC.
[5] Prime-counting function. Wikipedia. https://en.wikipedia.org/wiki/Prime-counting_function. Accessed September 20, 2023.
Request for a Letter of Recommendation for Submission to a Peer-Reviewed Journal:
To support the submission of this significant contribution, I kindly request a letter of recommendation from a qualified mathematician with expertise in the relevant field. The letter should be signed and written on official letterhead, confirming their understanding of the arguments presented in this paper and attesting to its correctness.
Please note that physical letters, not electronic, are required for submission and should be sent by regular mail. Thank you.
この記事が気に入ったらサポートをしてみませんか?
