ローレンツ対称性はすべての実験で破れている。
よく相対論を信じる人たちから、ローレンツ対称性は実験では破れてないから、破れてない内は相対論が正しいという言葉をよく聞く。本当に過去に破れている実験はないか? 調べてみたら、あるわあるわということで、紹介します。
まず、光速度が不変なら、等速直線運動で相対運動する者同士は、お互いの時計が遅れてみえるという時計仮説があります。
時計のパラドックス[編集]
今、ここに一組の双子がおり、二人は慣性運動しながら次第に離れているとする。このとき兄から見ると、弟の時計は遅れてみえ、逆に弟から見ると兄の時計は遅れてみえる事が特殊相対性理論から帰結される。これは一見奇妙に見えるため、時計のパラドックスと呼ばれることもあるが[39]、実は特に矛盾している訳ではない。なぜなら慣性運動している二人は二度と出会うことがないので、もう一度再会してどちらの時計が遅れているのかを確認するすべはないからである。
以上の二つは特殊相対性理論の説明として正しく、等速直線運動は紛れもなく慣性運動であり、お互いに時間の遅れが観測されると、光速度不変は正しいのです。
しかし時間の遅れは、本当にお互い様に見えるのでしょうか? それがはっきりする良い実験がありました。
以下の数式と図は以下参照、④相対論的ドップラー効果の検証実験
-マッカーサー(D.W.MacArthur)らの実験ー

相対論的ドップラー効果を利用して、Nd添加イットリウムアルミニウムガーネットレーザーの第4高調波光子のエネルギーを、800MeVの原子状水素(H0)ビームとの交差角θを変化させることで、移動する原子の基準枠内で1.4から15.8eVの範囲にシフトさせた。H0のよく知られたライマン転移(1sからnpまで)の交差角θを測定し、これらのデータをE=(E0/g0)γ(1+β cosθ)の式でフィットさせた。このようにして得られたE0/g0の値をレーザー光子のE0の測定値と比較すると、β〜=0.84でg0=1.000 04(27)が得られた。このようにして、g0=1という特殊相対性理論の予測は、2.7×10⁴の精度で検証された。
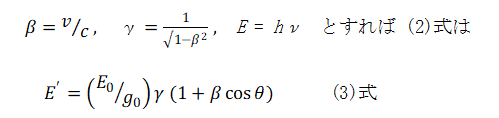
γ>1ですから、周波数が上がる=青方偏移するということです。あれ?慣性系同士ならお互い時間の遅れは赤方偏移になって観測されるのでは? 時間が早くなって観測されているじゃん。どうなっているの?
こんなに、はっきりした結果がでているのに反論した学者はいないか、調べました。
1907年に、アインシュタインは時間拡張を確証するために飛行原子を使った実験を提案しました。その論文では、飛ぶ原子は飛ぶ時計として考えられていました:ドップラー効果への言及は間接的でした(スタークによる実験の1次v / c)。1922年に、シュレーディンガーは(飛行)原子による光量子の放出がエネルギーと線形運動量の保存則によって規制されることを示しました。したがって、光子のドップラー効果は、原子と光子の間のエネルギーと運動量の交換の結果です。中心的な役割は、量子エネルギーのジャンプです。Δ E遷移の(相対論的不変量)。アインシュタインによって考案された実験の最初の実現は、Ives and Stilwell(1938)によるものです。それ以来、今日まで、この種の実験は、より良い精度および/または特殊相対論の予測からの逸脱を求めて繰り返されてきました。際立った特徴は、これらの実験を扱ったすべての論文がシュレーディンガーの力学的な扱いを完全に無視していることです。この省略の起源にはさまざまな種類があります:実用的(どこから来ても、公式間の合意と実験)、歴史的(光の波動理論の深い根づき)、および認識論的(基本的な認識論的ルールの無視)。
このシュレーディンガーがいう力学的な扱いが、慣性系→非慣性系→慣性系という慣性系間は非慣性系を挟まないと推移しないという、ニュートンやガリレオのいう慣性の法則(慣性系と非慣性系の区別を宣言)が正しい慣性系なんです。
ですが、実験で光速度不変を前提にしたお互いに時間が遅れて見える未慣性系はあり得なかったことが証明されているのに、無視されているのは悪質です。
マッカーサー(D.W.MacArthur)らの実験は、以下の(c)と同じで、反射が透過に変わっただけで、光行差がない分(c)より二次ドップラー効果がはっきりします。0.84cで運動する水素原子ビームの水素がたまに光子にエネルギーを与え、高調波に現れるのを計測している実験です。

5.相対論的速度で動く鏡からの光の反射 -レーザー・プラズマが作る航跡波からの電磁波の反射と周波数上昇-
相対論の場合は、こういう破れている実験を正しかったと言い張って誤魔化しているので要注意です。「相対論的力学のお互い様じゃない実験結果」は、「特殊相対論のお互い様の時計仮説」を否定しているのに、プロの学者に正しいと言われれば素人には区別つかないというか、そもそも基礎知識がないので騙しにしかなりません。
2つの相対論的仮説の意味は、それらの相反性と対称性の観点から分析されます。最初の仮説がすべてのフレームの完全な等価性を伴うのに対し、2番目の仮説は、アインシュタイン-ローレンツ方程式によって反映されるように、最初の仮説の等価性だけでなく実験の可能性とも衝突する値の(形式ではなく)非対称性を意味します検証。すべての具体的なケースで「非対称」です。これらの非対称性をより明確に示し、現実的な方法で4つの空間/時間変数の参照(物理)意味を解釈するために、最後に二重インデックス表記が提案されています。ローレンツとアインシュタインの相対性は対照的です。前者は非対称の実験的現実にうまく対応しているようです。
他にもあると思うので、見つけたらコメントください。
