電流素片ペアによって放射電磁界は遮蔽されているのか?(なぜアンテナから電波が放射するのか、検証うまくいってないけどいろいろとわかってきたよ編)
今回の目的
前回(といっても本当にだいぶ前)、アンテナが電磁界を放射する理由を探ったところ、電流があれば電磁界が放射するのがむしろ普通であり、電磁界を放射しないマイクロストリップのような線路の方が特殊なのではないかと考えました。そして、線路が放射しないのは電流の近くにはそれを打ち消すリターン電流があり、これによって放射電磁界が遮蔽されるのではと仮説を立てました。
そこでこの仮説が妥当なのかを検証するため、電流の打ち消しあいによる放射電磁界の遮蔽の効果を考えます。今回はモデルとして逆向きに流れる二つの平行微小電流が作る放射電磁界を考えてみることにしました。
原点に置かれた微小電流が作る放射電磁界
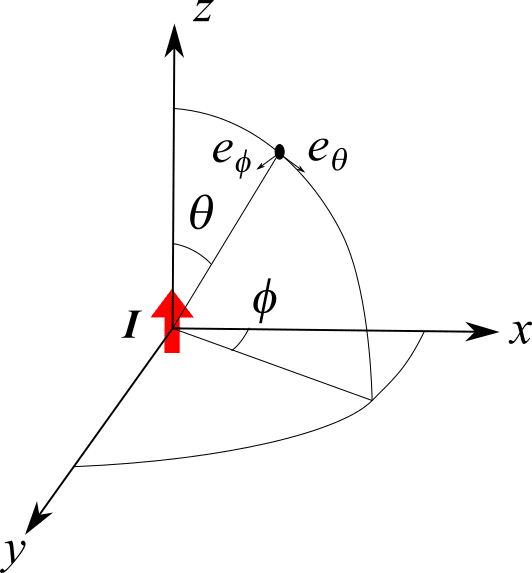
二つの平行微小電流について考えるために、まず原点に置かれた$${z}$$方向に流れる長さ$${L}$$の微小電流$${I=I_0 e^{j \omega t}}$$が作る電磁界についておさらいしましょう。このような微小電流の作る放射電磁界はさまざまな教科書やwebサイトに書いてあるので導出に関しては今回は省略しますが、特筆する点として今回は遠方界のみを考えるので$${1/r}$$に比例する放射界のみを考えるます。これは以下の式となります。電界は$${\theta}$$方向成分のみ、磁界は$${\phi}$$方向成分のみをもつことがそれぞれ$${\bm{e_{\theta}}}$$と$${\bm{e_{\phi}}}$$で表現されています。
$$
\bm{E} = \frac{\mu_0 I_0 L}{4\pi r} \bm{e_{\theta}} \sin{\theta} j \omega e^{j \omega (t-r/c)}\\
\bm{H} = \frac{I_0 L}{4\pi r} \bm{e_{\varphi}} \sin{\theta} \frac{j \omega}{c} e^{j \omega (t - r/c)}
$$
距離$${d}$$だけ$${x}$$方向に離れておかれた2つの逆向き平行微小ダイポール($${z}$$方向)が作る放射電磁界
前述の式をもとに$${z}$$方向に向いたそれぞれ逆向きに電流が流れる微小ダイポールのペアを考えます。$${x=d/2}$$に置かれた$${+z}$$方向に流れる微小電流が作る電界の$${\theta}$$成分を$${E_+}$$、$${x=-d/2}$$に置かれた$${-z}$$方向に流れる微小電流が作る電界の$${\theta}$$成分を$${E_-}$$としましょう。重ね合わせの原理から、電磁界はそれぞれのつくる電磁界の和になるので、その中で$${1/r}$$に比例する成分が逆向き平行微小電流のペアが作る放射電磁界ということになります。(次数の高いものは放射電磁界ではない)

$$
E_+ = \frac{j \omega \mu_0 L I_0}{4 \pi |\bm{r}-\bm{e_x}d/2 |} \sin{\theta} e^{j \omega t} e^{-j k |\bm{r}-\bm{e_x}d/2|} \\
E_- = \frac{-j \omega \mu_0 L I_0}{4 \pi |\bm{r}+\bm{e_x}d/2 |} \sin{\theta} e^{j \omega t} e^{-j k |\bm{r}+\bm{e_x}d/2|}
$$
$${x}$$軸上の観測点での電磁界
まず一番遮蔽されていそうな$${x}$$軸上(つまり、$${\theta=90 \degree}$$)の電磁界について考えてみましょう。ここで、$${\frac{1}{x-d/2} \approx \frac{1}{x} (1+d/2x)}$$という関係を用いると、以下のような式が得られます。
$$
E_+ + E_- \approx \frac{j \omega\mu_0 L I_0}{4 \pi} e^{j (\omega t- kx)} \times \frac{2j \sin(kd/2)}{x} +O(x^{-2})
$$
ここで、$${\tilde{I}=2 j \sin{kd/2} I_0}$$とすると、原点に置かれた微小電流$${\tilde{I}}$$が作る電界と同じになっています。つまり、$${x}$$軸上の観測点で見た場合、微小電流が極近くに置かれたペア($${kd<<1}$$)が作る放射電磁界は、原点に$${\tilde{I}= j k d I_0}$$の1つの放射ダイポールが作る放射電磁界で近似できることを示しています。なお、これは微小ループが作る放射電磁界と同じ議論にもなっています。

放射電磁界はダイポールを逆向きペアにしたことで弱くなっていますが、物理屋さんの観点から見ると、これをもって放射電磁界が遮蔽されたというのは違和感があります。物理屋さんの立場から電磁界が遮蔽されるといった場合、$${1/r}$$が$${e^{-\kappa r}/r}$$となる場合や、$${1/r}$$の項が打ち消しあって消えてしまい最低次数が$${1/r^2}$$又はそれよりも高次の項となることを指します。つまりこの結果は、「反対向きの電流が近くにあった場合でも放射界を遮蔽することはできず、$${1/r}$$で減衰する放射電磁界の強度は弱まるものの、依然として残ることがわかった」と言える結論です。つまり、議論の出発点であった、「反対向きの電流によって放射電磁界が遮蔽されるため、通常のマイクロストリップ線路などの伝送線路は放射しない」という仮説は正しくないということがわかりました。
一般の観測点$${\bm{r}=(x,y,z)}$$での電磁界
ついでに、$${x}$$軸上に限らず、一般の観測点での電磁界放射パターンを定性的に考えてみましょう。一般の観測点での受信電磁界はそれぞれのダイポールからの電磁界に対して光路差に応じた位相を考慮したうえで重ね合わせを考えればよいです。今考えている電流ペアは逆相なので、光路差$${d \sqrt{\cos^2 \theta + \sin^2 \theta \sin^2 \phi}}$$が$${\pi}$$であれば強めあい0であれば打ち消しあいます。ここで、最も光路差が発生する条件は実は$${x}$$軸上に観測点を置いたときとなり、前述のようにこの場合でも強め合う条件を達成できていません。そのため微小電流ペア同氏の距離が小さいときは任意の観測点で単独のダイポールによる電磁界よりも弱い電磁界放射が観測されることになります。

リターン電流が広く分布するような場合の電磁界
マイクロストリップラインは電磁界が放射しない回路ですが、なぜこれが電磁界を放射しないのか、という点で少し考えを推し進めてみます。マイクロストリップ線路のような場合、GND側は線路側よりも電流が広がっており、これによってGND側に電磁波が遮蔽されるのではないかとも考えました。それを検証するために下の図のような電流分布が作る電磁界を考えます。ここで$${n}$$はリターン側の電流を分割した数です。トータルの電流はちょうど打ち消しあっており、マイクロストリップ線路の断面の電流分布を大雑把に模擬したものになります。簡単のために$${z}$$軸上に限ってですが放射電界の強度分布を計算してみました。

このとき、$${d}$$や$${h}$$を変えたときの結果を以下に示します。なお、今回はグラフを作る際に縦軸をdB($${20 \log_{10} |E|}$$)で計算してしまっていることに注意してください。また、遠方界である$${1/r}$$の項のみを考えているので近距離でのふるまいの差は正しくないことにも注意し、遠距離での振る舞いを重点的に比較します。
まず、$${+z}$$方向($${z}$$軸上)への放射を比較してみます。GND電流が一点に集まった状態と広がった状態を比較するため、$${d}$$を変化させて放射電磁界を計算してみた結果が下の図です。遠方界、たとえば100mでの放射強度は-60dB付近とどちらも変わっておらず、GND電流が分布していることは放射電磁界に対して影響していないことが計算から確認できました。

次に、GND電流と配線電流の距離$${h}$$を変えたときの$${+z}$$方向の放射を比較した結果が下の図です。これは最初の議論(GND電流が広がっていない状態)で、電流ペアの距離を大きくしたことに対応しており、距離を話していくと放射電磁界が強くなっていることが図からも読み取れます。

最後に、GND電流を分割した時の$${-z}$$方向の放射と$${+z}$$方向の放射を比較した結果が下の図です。初め、分割されたGND電流によって放射が遮蔽されるため、$${-z}$$軸方向には電磁界が放射しないのではないかと考えていたのですが、実際にはそんなことは関係なく$${-z}$$軸方向も$${+z}$$軸方向と同じ程度に電磁界が放射されていることが計算からわかりました。

以上をまとめると、今回のモデルのようにリターン電流分を分割して考えたとしても遠方界での放射量は分割する前と変わらないことがわかりました。さらに、リターン電流を分割して考えてもGND側($${-z}$$側)と線路側($${+z}$$側)に放射する遠方界は同じ量であることもわかりました。
今回の結論
以上のことから、前回考えていた電流素片とリターン電流がペアで存在することで放射電磁界を遮蔽するため放射しなくなると考えることは、放射量が減ることは確かながら、放射はするということがわかりました。
また、なぜマイクロストリップラインは電磁界が放射しないのか、を考える手がかりとしてその電流分布を模擬したモデルを構築しその放射を考えてみました。しかし、このモデルでも電磁界の放射を止めることはできず、さらにGNDがある$${-z}$$方向の放射電磁界が$${+z}$$方向の放射電磁界と量的に一致するという実際とは絶対にありえない状況が計算結果として現れることもわかりました。このことは、今回のモデルがマイクロストリップラインが放射しない理由を説明できないモデルとなっており、必要なエッセンスが抜けたモデルであるということです。なお、今回のモデルで不足していることとしては、GND面の存在による電磁界の境界条件があると考えており、これを使ってマイクロストリップラインが放射しない原理を(自分が納得できるような)説明ができるように理論構築をしたいと考えております。
この記事が気に入ったらサポートをしてみませんか?
