
🎲確率質量関数(PMF)と期待値の関係について教えてください
確率質量関数(probability mass function, PMF)と期待値の関係について説明します。確率質量関数は、離散確率変数が取り得る各値に対して、その値を取る確率を割り当てる関数です。一方、期待値(expected value)は、確率変数が取り得る値とその値を取る確率の積の総和であり、確率変数の平均的な値を示します。
離散確率変数 X の確率質量関数を f(x) とするとき、X の期待値 E[X] は以下のように計算されます:

ここで、和は X が取り得るすべての値 x にわたって計算されます。つまり、期待値は、各値とその値を取る確率の積を全て足し合わせたものです。
例えば、サイコロを投げる場合、確率質量関数はすべての面(1から6まで)で 1/6 です。期待値は以下のように計算できます:

この結果は、サイコロを非常に多く投げた場合に平均して得られる値が3.5であることを意味します。サイコロの例のように、期待値は必ずしも確率変数が取り得る実際の値ではありませんが、その確率分布の平均的な傾向を示します。
要するに、確率質量関数と期待値の関係は、確率質量関数が各値を取る確率を提供し、それを用いて期待値が計算されるという点にあります。期待値は、確率変数の平均的な振る舞いを数値的に表すものです。
コイントスはベルヌーイ分布ですか?
はい、コイントスはベルヌーイ分布の典型的な例です。ベルヌーイ分布は、結果が2つだけの実験(例えば、成功/失敗、表/裏など)に使用される離散確率分布です。コイントスの場合、コインが表か裏のいずれか一方を示すという2つの可能な結果があります。
コイントスの各試行はベルヌーイ試行とみなすことができ、結果が「表」である確率(通常 p と表される)と「裏」である確率(1−p)がそれぞれ確率質量関数によって与えられます。理想的なコインの場合、p=0.5 です。ベルヌーイ分布の確率質量関数は以下のようになります:

ここで x は成功(x=1、例えば「表」)か失敗(x=0、例えば「裏」)を示す値です。
裏と表の二値しかないから、自ずと片方の確率が分かれば、もう片方も決まるんだよ、と言ってる式ということでしょうか?
はい、正確にその通りです。ベルヌーイ分布において、結果が2つしかない場合(例えばコイントスの裏または表)、片方の結果が起こる確率 p を知れば、もう片方が起こる確率は自動的に 1−p となります。この性質はベルヌーイ分布が表す基本的な原理です。
シャノンの情報理論の式も似たものがつかわれてませんでしたっけ?
はい、シャノンの情報理論における情報量(エントロピー)の式は、ベルヌーイ分布の確率質量関数と形が似ています。エントロピーは、情報の不確実性または乱雑さを定量化するもので、次のような式で表されます。

H(X) は離散確率変数 X のエントロピー、
n は X が取りうる異なる値の数、
p(xi) は変数 X が特定の値 xi を取る確率、
loglog は対数関数(底は通常2で、ビット単位の情報量を意味します)。
この式は、各可能なイベントの発生確率にその確率の対数を乗じたものを合計しています。ベルヌーイ分布の場合のエントロピーは二値の結果に対する式となり、次のように簡単化できます。
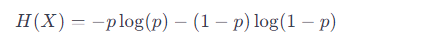
def bernoulli_pmf(p, x):
"""
ベルヌーイ分布の確率質量関数を計算する関数。
引数:
p -- 成功(表が出る)の確率。
x -- 試行の結果(1: 成功/表, 0: 失敗/裏)。
戻り値:
与えられたxの値に対する確率。
"""
return p**x * (1-p)**(1-x)
# 表が出る確率を0.25として設定
p = 0.25
# 表が出る確率(x=1)と裏が出る確率(x=0)を計算
probability_heads = bernoulli_pmf(p, 1) # 表
probability_tails = bernoulli_pmf(p, 0) # 裏
print(f"表が出る確率: {probability_heads}")
print(f"裏が出る確率: {probability_tails}")
お願い致します
