ウントリセプチウムとウンセプトトリウム

2024年6月25日 04:33

この2つ、混同しやすいけど全く違うよという話。あと真空崩壊のお話。

限界の原子番号

元素を原子番号順に並べます。水素、ヘリウム、リチウム、ベリリウム … と続きます。どこまで続くでしょうか。日本で発見されたニホニウムは原子番号113です。現在のところ原子番号118のオガネソンが公式に認められた最大の原子番号の原子のようです:

さて、理論的に予測される原子番号の上限値はどのくらいでしょうか。

このとき以下の2つを区別してください：

原子核そのものの存在可能性。強い相互作用の計算を必要とする
原子核の存在を仮定した上での安定な電子・電子軌道の存在可能性。電磁気力のみが関わる計算

1.は原子核そのものを計算対象とします。重い原子核では例えば液滴モデルや殻模型と呼ばれる有効模型を用いて系のエネルギー準位等が計算されますが、本記事の主題ではないので（かつよくわからないので）省きます。

本記事では2.を対象として述べたいと思います。　実はたとえ原子核は安定して存在したとしても、そのまわりに電子が安定して存在できるかどうかは別問題なのです。表題の「ウントリセプチウム(untriseptium)」と「ウンセプトトリウム(unsepttrium)」はそれぞれ原子番号137および173の原子の仮の名前ですが、これらは原子核の存在を仮定したとき、2つの違う理由で電子が不安定になると考えられている限界の原子です。正確に言うと

ウントリセプチウムは電子が原子核に落ち込んでしまう限界の原子
ウンセプトトリウムは真空から電子と陽電子が対生成される限界の原子

です。前者の原子番号$${Z}$$は$${Z=137}$$、後者が$${173}$$です。$${137}$$が限界ならば後者はそもそも存在できないのでは？と思うかもしれませんが、のちに述べるように原子核の拡がりを考慮すると$${137}$$より大きい原子番号も存在できるのです。

あと、これらは原子番号の上限であることに注意してください。この番号より小さい原子番号の原子が必ず存在するというわけではないです。

この2つの原子における電子の不安定性は根本的に異なります。特に後者の不安定性はかなり不思議なものです。

以下これらについて述べていきます。

前提その1: 古典的には原子は安定しない

宇宙開闢の後しばらくは電子と原子核は別々に存在し、電子は宇宙にガスのように漂っていました。そのため光は電子ガスに散乱されまっすぐ進めず霧がかかったような状態だったと考えられています。しかし宇宙膨張により宇宙の温度が下がると、ある時点で電子は原子核のまわりに囚われます。電子ガスが消失したことで光がまっすぐ進めるようになり霧が晴れます。これは宇宙の温度が$${3000\mathrm{K}}$$まで下がった頃、宇宙開闢から38万年ほど後のことで、「宇宙の晴れ上がり」と呼ばれます。以下のページが詳しいです:

こうして電子は原子核の周りを"回る"ようになりました。しかし円運動をすると電子は電磁波を放出するはずです。荷電粒子の加速度運動による電磁波は実験でも利用されています。東北大学のキャンパスにある次世代放射光施設"NanoTerasu"は、それを利用して非常に強い光を作る施設です:

電磁波を放出すればその反作用で電子は遅くなります。放射光施設ではクライストロンという装置により電子を再加速するそうです。

もし電子が原子の周りを回転しているなら、加速装置がない原子では電子は電磁波を放出し一瞬にして原子核の中に落ち込んでエネルギー的に安定な状態になるはずです。これでは宇宙の晴れ上がりが起こったとたんに電子は原子核に吸収されてしまいます。しかし実際の原子の電子軌道は安定であり、かつ原子核の大きさと比較し遥かに大きな軌道上に存在します。野球場のピッチャーマウンドにある10円玉が原子核だとすると、電子軌道は球場の外周くらいのスケール感です。

原子核のまわりを電子が"回る"という描像は、なんだかおかしいです。

前提その2: 原子は量子論で安定する

前章の原子は古典的な描像です。量子論では話が異なり、原子は安定します。

これには良く知られた直感的な説明が存在します（Ref.[1]）。それは不確定性原理によります。不確定性原理とは、量子論に従い運動する物体の位置と運動量の不確定さに関する以下の関係です：

$$
\Delta x\Delta p \sim\hbar
$$

本記事の文脈では、$${\Delta x}$$は原子における電子の波動関数の広がり（位置の広がり）、$${\Delta p}$$は電子の運動量の不確定性（運動量の広がり）だと思ってください。$${\Delta x,\Delta p}$$の両方をゼロにすることはできず、その積がおおよそ$${\hbar}$$くらいは不確定である、ということを表します。

これを用いてなぜ量子論で原子が安定になるかを大雑把に説明します。原子のエネルギーを表すハミルトニアンは以下で表されます：

$$
H=\frac{\hat p^2}{2m}-\frac{Z\alpha}{r}
$$

ここで光速$${c}$$と換算プランク定数$${\hbar}$$は$${c=\hbar=1}$$にしています（=自然単位系を採用している）。第1項は電子の運動エネルギー、第2項は原子核がつくる電場による電子のポテンシャルエネルギーです。$${\alpha}$$は微細構造定数と呼ばれる定数であり、およそ$${1/137}$$です。$${Z}$$は原子番号であり、原子核の電荷は$${-Ze}$$（$${e}$$:電子の電荷）です。量子力学では運動量$${\hat p}$$は演算子で、$${\hat p=-i\partial/\partial x}$$です。

$${\hat p}$$は演算子ですが、その電子の波動関数による期待値を$${p}$$で表しましょう。そして$${r}$$を、不確定性関係を用いて

$$
r \simeq 1/p
$$

で大雑把に見積もりましょう。これは不確定性の下限ではあるのですが、エネルギーが低い状態の波動関数は不確定性が小さいと期待します。これをEq.(1)に代入すれば

$$
H(p)=\frac{p^2}{2m}-Z\alpha p
$$

となります。エネルギー最小の状態（=ハミルトニアン最小の状態）を考えます。これが実際に実現される状態です。$${H(p)}$$の$${p}$$に関する最小値は$${p=Z\alpha m}$$で実現し、$${H(p)|_{p=Z\alpha m}=-\frac{1}{2}\alpha^2 Z^2m}$$となります。波動関数の広がり$${r\simeq 1/p}$$は$${(Z\alpha m)^{-1}}$$程度であり、有限の値を持ちます。そのため、電磁波の放射の効果を考えたとしても、この状態がすでにエネルギー最小なので安定です。

古典論の何がいけなかったかというと、原子核に電子が落ちた状態が運動エネルギーもポテンシャルエネルギーも最も低い状態であったことです。これにより、電磁場との相互作用を考慮し開放系になると、回転分だけエネルギーの高い電子はそれを失い原子核に落ちます（図1）。これに対し、量子論では電子が原子核に落ちると不確定性原理により運動エネルギーが高くなってしまいます（図2）。ある程度原子核のまわりに「ふわッと」存在している方が全エネルギーが低くなるのです。

エネルギーをキチンと計算するには、ハミルトニアンの固有値・固有状態を$${H\psi=E\psi}$$を解くことで求める必要があります。しかしながら、いい加減な見積もりであるにもかかわらず、上記したエネルギーの見積もりは厳密な計算による水素原子の基底状態のエネルギー

$$
E_0=-\frac{1}{2}\alpha^2 m \simeq -13.6\mathrm{eV}
$$

を再現します。

ウントリセプチウム

しかしこの安定性も、相対論を考慮すると限界があります。その臨界値が$${Z=137}$$です（Ref.[2][3]）。ウントリセプチウムが限界の原子と呼ばれる所以です。

直感的な説明その1

ウントリセプチウムが限界である最も簡単な説明は、$${p=mv}$$としたとき、$${Z=137}$$になると、前章の見積もりでエネルギーが最小となる$${p}$$において$${v}$$が光速に達するというものです。実際エネルギーを最小にする速度は上記の計算において$${v=\alpha Z}$$となり、$${Z>1/\alpha\simeq 137}$$で$${v}$$は1を超えます。自然単位系ではこれは電子の速度が光速を超えることを意味します。相対論では電子の速度が光速を超えることは禁止されるので、$${Z>137}$$の原子は存在できないことになります。

直感的な説明その2

もうすこしマシな見積もりをします（Ref.[2]）。

相対論では、運動量と運動エネルギーの関係が非相対論の場合と変わり

$$
E^2=p^2+m^2
$$

になります。これを用いて、相対論的な運動をする電子に対する原子のハミルトニアン、運動エネルギー＋ポテンシャルエネルギーを

$$
H=\sqrt{p^2+m^2}-\frac{Z\alpha}{r}
$$

としましょう。前と同様$${r\simeq 1/p}$$とします。ここで$${p}$$が$${m}$$に対して非常に大きい場合を考え

$$
\sqrt{p^2+m^2}\sim p
$$

にします。すると$${H}$$は

$$
H(p)\sim (1-Z\alpha)p
$$

になります。ここでもし$${1-Z\alpha<0\leftrightarrow Z>1/\alpha}$$なら、$${H(p)}$$は$${p}$$に対する最小値を持たず、$${p}$$が大きくなればなるほど系のエネルギーは小さくなります。すなわち$${Z>1/\alpha\simeq 137}$$では、$${r\simeq 1/p}$$は小さければ小さいほど系のエネルギーは小さくなるため（運動エネルギーの損をポテンシャルエネルギーの得が上回る）、電子は原子核に落ち込みます（図3）。

ここでの見積もりもまたいい加減ではあるのですが、Eq.(2)において$${\partial H(p)/\partial p=0}$$を実現する$${p}$$におけるエネルギー$${m\sqrt{1-\alpha^2 Z^2}}$$は、相対論的な量子力学における厳密な水素原子の基底状態のエネルギーを再現します。$${m\sqrt{1-\alpha^2Z^2}}$$が$${Z>1/\alpha}$$で虚数になるのは、そのような$${Z}$$で電子は安定した状態にないことを示しています。

正確な計算

正しくウントリセプチウムを扱うには、水素様原子（ただし原子核の電荷は$${-Ze}$$）に対するエネルギー$${E}$$と波動関数$${\psi}$$の方程式

$$
H\psi = E\psi, \ \ \ H=-i\hbar c\boldsymbol{\alpha}\cdot\boldsymbol{\nabla}+mc^2\beta-\frac{Z\alpha\hbar c}{r}\\
$$

を解く必要があります（Ref.[2][3]）。これはディラック方程式と呼ばれます。最後の項の$${Z,\alpha}$$は前章に現れた量、$${c,\hbar}$$はそれぞれ光速と換算プランク定数、$${r}$$は原子核から電子までの距離、$${\boldsymbol{\nabla}}$$は空間微分：$${\boldsymbol{\nabla}=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})}$$です。第1・2項に現れる$${\boldsymbol{\alpha},\beta}$$は4行4列の行列であり、それぞれ

$$
\alpha_i=
\begin{pmatrix}
0 & \sigma_i\\
\sigma_i & 0
\end{pmatrix}
, \ \beta=
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
\\
{}
\\
1,0\text{は2行2列の単位行列とゼロ行列}。\sigma_i\text{はパウリ行列}\\ {}\\
\sigma_1=
\begin{pmatrix}
0&1\\1&0
\end{pmatrix}
,
\sigma_2=
\begin{pmatrix}
0&-i\\i&0
\end{pmatrix}
,
\sigma_3=
\begin{pmatrix}
1&0\\0&-1
\end{pmatrix}
$$

です。ディラック方程式を解くのはそれなりに大変ですが、計算するとエネルギー準位が

$$
\begin{aligned}
&E=\frac{mc^2}{\sqrt{1+\frac{Z^2\alpha^2}{\left(n-(j+1/2)+\sqrt{(j+1/2)^2-Z^2\alpha^2}\right)^2}}},\\
&n=1,2,3,\cdots,\\
&\text{与えられた}n\text{に対し}j=1/2,3/2,\cdots,n-1/2
\end{aligned}
$$

となります（Ref.[2][3]）。もっともエネルギーが低くなるのは$${n=1,j=1/2}$$のときであり、そのエネルギーは

$$
\begin{aligned}
&E=mc^2\sqrt{1-Z^2\alpha^2}
\end{aligned}
$$

になります。これは前章の結果と一致します（前章の議論は自然単位系であることに注意）。そして$${Z>1/\alpha\simeq 137}$$のとき平方根の中が負になり、安定解が存在しません。

この計算では原子核は$${-Ze}$$の電荷をもつ点電荷であるという点に留意してください。

ウンセプトトリウム

ウントリセプチウムの計算では原子核は点電荷として扱われました。実は原子核の大きさを考慮すると電子軌道は安定して存在できることが知られています（Ref.[4][5]）。よってウントリセプチウムは「原子核の拡がりを考慮しなかったことによるartifact」ともいえます。ただ、その電子軌道の大きさは通常の原子よりかなり小さいのではないかとは思いますが…

では原子核の拡がりさえ考慮すれば、どんな$${Z}$$でも安定な電子軌道が存在するのでしょうか。実は$${Z}$$が173くらい大きくなると、非常に不思議な、大げさに言えば世界観が変わるような現象が起こることが予想されています。

この粒子にまつわる物理に関して以下説明します。

ディラックの海

まずディラックの海を説明します。前章で現れたディラック方程式の解には負のエネルギー解があります。エネルギーは原点の取り方によるので、原点をずらせば正にできるのでは？と思われるかもしれません。しかしこの負のエネルギー解は原点の取り方では除けません。なぜなら解は正負対称に存在するからです。ある正のエネルギー$${E}$$をもつ状態が存在するなら、必ず$${-E}$$の状態が付随して現れてしまうのです。しかも負のエネルギー解を無視するわけにもいきません。なぜなら負のエネルギー解は因果律を保つために必要だからです（Ref.[2]）。

しかしエネルギー負の状態を受け入れるのも問題があります。世の中はエネルギー最小な状態でできています。ところが上記の負のエネルギー状態には底がありません。エネルギー正の状態に上限がないから、その符号を反対にした$${-E}$$もいくらでも負に小さく（絶対値は大きく）なります。これでは電子は光を放出しながら無限にエネルギーの低い状態に落ち込んでしまいます。1つの電子から光が無限に放出されるでしょう。

この矛盾を解決するのが「ディラックの海」です（Ref.[2]、図4）。

ディラックの海の描像では、真空とは負のエネルギー状態が電子で埋まっている状態です。電子はフェルミオンと呼ばれる粒子であり、これは同じエネルギー状態には1つしか入れない排他的な粒子です。負のエネルギー状態はすでに埋まっているので、それ以上電子が落ちることはありません。重要なのは真空の負のエネルギー状態を埋めている電子は観測できないことです。この状態が「何もない」状態なのです。

一方、真空に存在する電子にエネルギーを与えて正のエネルギーに励起させると、負のエネルギー状態に穴があきます。正のエネルギーに励起した電子はもちろん観測できますし、かつ負のエネルギー状態に空いた穴も観測できます。後者が反電子、すなわち陽電子です。つまりこれは真空から電子・陽電子の対生成が起こる過程に対応します（図4）。

ひとつ重要なことがあります。電子はもともと質量エネルギー$${m_ec^2}$$を持ちます。また正負のエネルギー状態の対称性があります。そのため$${E=-m_ec^2}$$から$${m_ec^2}$$の間には電子は存在できません。よって負のエネルギー状態の電子を正エネルギーに励起させるには、最低でも$${2m_ec^2}$$のエネルギーが必要です。

Z>173で起こること

水素原子の最も低いエネルギー状態は

$$
E_0=-\frac{1}{2}\alpha^2 m \simeq -13.6\mathrm{eV}
$$

でした。これは、この状態の電子を原子核から無限に遠くに引き離すのに必要なエネルギーが$${13.6\text{eV}}$$ということです。つまり、電子が1つ原子核の電場の影響を受けずに存在しているときにくらべて$${13.6\text{eV}}$$だけエネルギーの低い状態にあるということです。電子が1つ静止して存在しているときのエネルギーはディラックの海で言えば$${E=m_ec^2}$$なので、図4では水素原子の電子のエネルギーは

$$
E=m_ec^2-E_0\simeq (510999.0-13.6)\text{eV}
$$

に位置します。これは正エネルギーのしきい値よりほんのちょっと低い値です。

ここで$${Z}$$を大きくします（図5）。原子核の大きさを考慮しない場合、ウントリセプチウム（$${Z=137}$$）になるとその基底状態のエネルギーが$${E=0}$$になります。すなわち束縛エネルギーが電子1つぶん、$${m_ec^2}$$になります。原子核の大きさを考慮するとこれがずれて$${Z=150}$$あたりで$${E=0}$$になります。

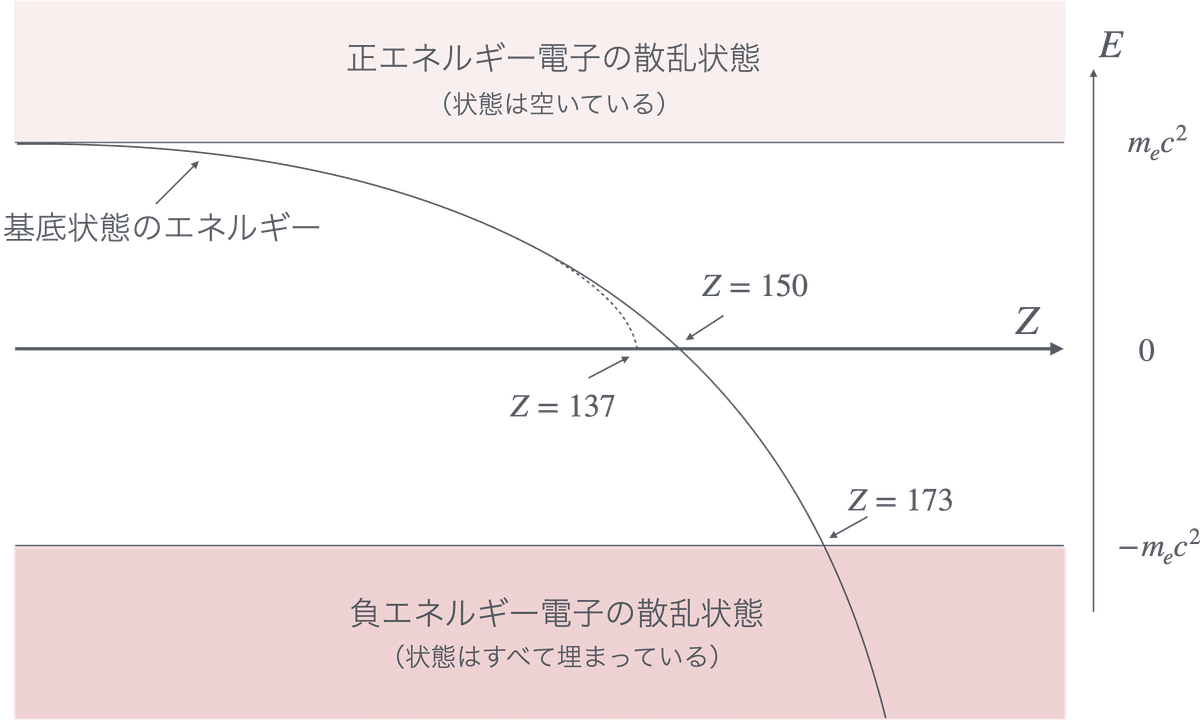
図5: ディラックの海と水素様原子の基底状態のエネルギー（実線カーブ）。Z=137付近の点線は原子核を点とした場合の基底状態のエネルギー。実線の計算では原子核の大きさを考慮している。

もっと$${Z}$$を大きくすると、基底状態のエネルギーは負のエネルギーに落ち込みます。そしてウンセプトトリウム（$${Z=173}$$）に至り、エネルギー準位が負の電子が存在するしきい値より低くなります。このとき状況がガラッと変わります（Ref.[4][5][6][7]）。

いまこの粒子の基底状態には電子が存在しないとしましょう。このとき何が起こるかというと、真空の負のエネルギー準位に存在する電子が原子核の作る電場による基底状態の準位に移ります（図6）。そして真空に空いた穴が陽電子として観測されます。つまり$${Z}$$がこれほど大きくなると、原子核の電場は真空の負のエネルギー状態に存在する電子を引きずり出して基底状態の準位を埋め、対で生まれた陽電子は原子核の外に放出されます。スピン状態がアップとダウンの2つあるので、基底状態が空いていると2つの電子が海から入り込みます。そして2つの穴=2つの陽電子が生まれます。原子核のつくる電場によるこのような真空の性質の変化を「真空崩壊」と呼びます。

この電子・陽電子は実粒子であることに注意してください。真空では電子・陽電子が常に対生成しているということがありますが、それはいわゆる仮想粒子であり、on-shell条件：$${E^2=m_e^2+p^2}$$を満たしません。そのような粒子はごく一瞬しか存在できません。一方$${Z>173}$$で生じる電子と陽電子はon-shell条件を満たし、未来永劫存在します。

このような原子核の実際の計算はそれほど単純ではないです(Ref.[5])。ディラック方程式を解く際には原子核の大きさを考慮しなければならないし、場の量子論の効果も存在します。しかも電場が強いため、単純な摂動的扱いもできません。さらに実験と比較するためには動的な過程も計算しなければなりません。ドイツおよび旧ソ連のグループはこのような計算を様々な観点から詳細に行い（特にドイツのW.Greinerらのグループ）、様々な効果を考慮してもこの現象の起こる臨界の原子番号$${Z_\text{cr}}$$は数%変化する程度であり、このような極限的な原子核が$${Z=173}$$付近に存在することを理論的に示しました。

しかしいづれにせよこれほど大きな$${Z}$$をもつ原子は存在しません。そこで鉛やウラン等の$${Z}$$の大きい原子核をぶつけることで、大きな$${Z}$$の状態を有効的に実現する実験が提案され、実際に行われました。残念ながら現在までに真空崩壊の確実な証拠は得られていませんが（脚注2）、今後もドイツ、中国、ロシア等で真空崩壊を捉える実験が計画されているようです（Ref.[7]）。

ちなみにこのような真空崩壊は、強い一様電場による電子-陽電子の対生成現象であるSchwinger効果や、ブラックホールの事象の地平における粒子の対生成によるHawking輻射と類似の現象です（Ref.[7]）。しかしながら現在まで、これらの現象は私の知る限りでは実験的に発見されていません。有効的に造られた$${Z>173}$$の原子核による自発的な陽電子放出が確認されれば、真空の崩壊現象の初めての観測例となるかもしれません。ちなみにホントの真空ではないですが、物性系では類似現象は確認されています。

加速器で粒子をぶつければ粒子・反粒子が生成されます。このようなダイナミカルな過程での対生成はふつうに観測されています。宇宙から地球の大気に飛び込んでくる宇宙線でも反陽子はたくさん作られており、霧箱やスパークチェンバーという装置があれば簡単に観測できます。これらは真空ではなくその上の励起状態のダイナミクスによる現象です。ウンセプトトリウムが特別なのは、対生成が、大きな電荷をもつ原子核がただ存在するという静的な状況で自発的におこる点であることに注意してください。これは真空の性質を直接反映した現象です。

相対論的な量子力学や場の量子論では、真空はなにも起こらなくて面白みのない状態ではないです。真空が物質に影響し、また逆に物質が真空に影響します。状況次第で実粒子さえそこから生成されます。この記事の話は電磁気学の話ですが、弱い相互作用におけるヒッグス凝縮を伴う真空、また強い相互作用におけるカイラル対称性の自発的破れおよびカラー閉じ込めの起こる真空はさらに非自明で複雑な構造を持ちます。

おしまい。$${{}_\blacksquare}$$

【脚注1】晴れ上がり時に解放された光が宇宙背景放射（Cosmic Background Microwave, CMB）です。そのスペクトルは2.7Kの黒体輻射のプランク分布ときれいに一致します。この温度は宇宙膨張の影響により、宇宙の晴れ上がり当時の温度より遥かに低いことに注意してください。CMBはどこでも観測しようと思えば観測できます。電波を受信するタイプのテレビでは、局が存在しないチャンネルに合わせると「砂嵐」が見えますが、その中にはCMBによる「砂」が時折存在しているそうです。

【脚注2】1980年にドイツのGSIという研究所で行われたウランとキュリウムの衝突実験において、陽電子スペクトルに鋭いピーク構造が観測されました（Ref.[4][6]）。これが真空崩壊による陽電子なのか検討されましたが、理論計算ではピークがもっと広くなだらかになるとのことで、現在まで真空崩壊の証拠とはみなされていないようです。

参考文献

猪木慶治, 川合光, 「量子力学 I」, 講談社サイエンティフィック (1994).
西島和彦, 「相対論的量子力学」, 新物理学シリーズ13, 培風館 (1973).
日笠健一,「ディラック方程式 −相対論的量子力学と量子場理論−」, SGCライブラリー 105, サイエンス社 (2014).
Greenberg, J. S. and Greiner, W., "Search for the sparking of the vacuum," Phys. Today 35, 24–32 (1982).
Reinhardt, J. and Greiner, W., "Quantum electrodynamics of strong fields," Rep. Prog. Phys. 40, 219 (1977).
中山康之, 伊藤真, 「真空は崩壊するか」, 日本物理学会誌第38巻第10号 (1983).
Ruffini, R., Vereshchagin, G. and Xue, S.-S., "Electron–positron pairs in physics and astrophysics: From heavy nuclei to black holes," Phys. Rep. 487, 1–140 (2010).