2024/04/09　九州大学文系数学を解いてみた2024

はじめに

　毎日投稿９日目です。今日は２０２４年度の九州大学文系の数学の問題を解説し感想を述べます。思いのほか図の作成に時間がかかり、地の文を打ち始めたのが２３時２０分です。とりあえず５５分くらいまで文章を書いていったん投稿して記録を続けたことにして、その後再編集で続きを書ききってから寝たいと思います。とりあえず記録を途切れさえないことが何よりも重要です。

　ということで、まずは問題文からいきましょう。興味がある方はまず解いてみてから僕の答案に進んでもらえたらと思います。全部で４問あります：

第１問と第２問（後者の問題文を修正しました）

第３問と第４問

　それでは解説に入ります。

第１問　二つの放物線と共通接線。⑴は微分なしでも解ける。

文系にも $${(x - a)^n}$$ の積分公式は教えるべきだと思います（断りなく使っています）。

　２次関数の共通接線に関する微積分の総合問題です。極めて典型的な問題で、そのまま教科書に載っていそうな感じがしますので、試験では落としたくありませんね。

　２次関数に限らず、同時に異なる２つの曲線 $${C_1 : y = f(x)}$$ と $${C_2 : y = g(x)}$$ に接する直線の求め方として、

• $${C_1}$$ の $${x = t}$$ における接線 $${y = f'(t)(x - t) + f(t)}$$ が $${C_2}$$ にも接するとして、連立方程式
  　　　$${g(x) = f'(t)(x - t) + g(t)}$$
  が重解を持つ条件を考える。

• $${C_1}$$ の $${x = t}$$ における接線
  　　　$${y = f'(t)(x - t) + f(t)}$$
  と $${C_2}$$ の $${x = s}$$ における接線
  　　　$${y = g'(t)(x - s) + g(s)}$$
  が一致するとして、傾きと切片を比較する。

の２通りが考えられます。前者の「連立方程式が重解を持つ条件」を求めるのは基本的に難しいですが、$${g(x)}$$ が $${2}$$ 次式である場合には判別式に着目して処理できます。特に高校生は判別式を使うとなぜかピンときやすい傾向があるので、こちらの解法をとるのがよいでしょう。文系数学でよくあるのは、$${f(x)}$$ が $${3}$$ 次式で $${g(x)}$$ が $${2}$$ 次式のケースで、この場合は $${C_1}$$ の接線が $${C_2}$$ に接するとすればスムーズです（これを逆に「$${C_2}$$ の接線が $${C_1}$$ に接する」とやると $${3}$$ 次方程式が重解を持つ条件を考察することになり厳しいです）。

　後者の解法は別解１として紹介しています。処理量もさほど変わらないので、この問題をどっちで解くかは完全に好みの問題です。前者の解法と比べて優れているのは、前者が $${2}$$ 次関数を含む場合に限ったものであるのに対し、一般の関数の場合にも適応できる汎用性の高さです。試験場では微積分を得点源としたいところですので、汎用性の高い解法で機械的に処理するのも一つの手でしょうね。

　ちなみに、二曲線の位置関係の特殊性（頂点が再び元の曲線に載るように平行移動する）により、微分を使わずに解くこともできてしまいます。これは趣味程度に眺めてもらえればと思います。

　⑵については、$${C_1}$$ と $${C_2}$$ の交点で積分を分けて考えることに注意して丁寧に計算します。その際、接点の $${x}$$ 座標において $${2}$$ 乗でくくる因数分解が成り立つことに注意して、厳密には数学Ⅲで扱う不定積分の公式
　$${\displaystyle \int (x - a)^n dx = \frac{(x - a)^{n + 1}}{n + 1} + C}$$
を用いると計算が楽になります。文系の生徒にもこれは教えたほうがいいと思うんですけどね。何ならこの問題を題材として置換積分（平行移動）の要領で教えてしまうのも手かもしれません。

第２問　図形的に見ることができれば計算量を大幅に減らせる。

どう解いても計算が複雑にならないのが素敵。今年一の良問かもしれません。

　これも何度的にはそれほど高いわけではなく、ガリガリ計算すれば答えを出すことはできるかと思いますが、ただ「ガリガリ計算するだけ」で終わらせるには惜しい、極めていい問題だと思います。最初から初等幾何的な考え方が思いつかなかったとしても、計算して $${s = t}$$ を導いてからその意味を考えることで「そうか半直線ＯＭ上にあるのか」と気づけます。

　特に⑵を考察する上で「ＯＡとＡＢが直交している」というのは見逃せない大事な条件になります。三角形の面積を考察する上で直交している $${2}$$ 辺があったら、それを底辺と高さと見ることができないか、と考えてみるわけですね。そうすると、点Ｃが辺ＡＢ上にあるとすればその中点であると見抜くことができ、あとはＯＭ上を動かせば面積が等しくなると考えられます。どちらかというと高校受験で見たような考え方かもしれません。

　また、３点Ａ、Ｂ、Ｃの座標成分がわかっていることから、座標の面積公式
　　$${\displaystyle S = \frac{1}{2} | ad - bc |}$$
を使ってしまうのも手ですが、僕としては文系の子がこの公式を覚えているべきかというと微妙なラインに思えました。行列式の話に繋がることから理系の子にはぜひとも覚えておいてほしいんですが、ここでは別解とすることにしておきます。また、辺ＯＡ、ＯＢが底辺に見えた人にとっては、点Ｃかた下ろした垂線の長さを高さと見て、点と直線の距離の公式を使って導くという方法もあるかと思います。

第３問　不定方程式に大小関係を持ちこむ典型例。誘導がいい。

　階乗を含んだ不定方程式の整数解を考える問題です。⑴は当たり前っぽくてどう説明するのか難しいかもしれませんが、多くの子は
　$${\displaystyle \frac{b!}{a!} = b(b-1) \cdots (a + 1) \geqq b \overbrace{1 \cdots 1}^{b - a - 1 \ 個}  \geqq b}$$
とやったのではないでしょうか。この問題は解くことよりも⑵や⑶にどう生かすかを考えてほしい、という手の誘導ですね。⑴を踏まえれば⑵の両辺を $${a!}$$ で割ってみようと自然に思えるのではないでしょうか。問題は⑶にどこまで手を付けられるかでしょう。

　例えば、数学Ａでよくある不定方程式の問題として
　　$${\displaystyle \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 1}$$
とを満たす自然数の組 $${(a, b, c)}$$ を求めよ、というやつがあります。特にこの手の問題では「$${a < b < c}$$」という条件が一緒に与えられることが多いかと思いますが、これがまさに「等式の問題ではあるが不等式を使って範囲を絞る」という手法の一例になっています。ここにある２つの壁として

• 等式の問題を考えていたはずなのに不等式がどこからか出てきて狐につままれた気持ちになる（特に普通の高校生は不等式が苦手なので、嫌悪感が増してしまう）

• 問題集の解答に「対称性から $${a \leqq b \leqq c}$$ としてよい 」「$${a \leqq b \leqq c}$$ としても一般性を失わない」などと書かれていて「対称性とか一般性を失わないって何やねん」となってしまう

といったことが挙げられると思います。特に前者の気持ちは「（必要十分）条件を考えるときにまず必要条件から吟味する」という手法でも近しい感覚を味わう子が多い気がします。ここは慣れかもしれませんが、できるだけ不等式を持ち出す必然性（自然だと思える感覚）が伝わるよう教えたいところです。たとえば極端ですが
　　$${\displaystyle \frac{1}{a} + \frac{1}{b} = 10}$$
を考えてみると「左辺はそんなに大きくならない（不等式的な感覚！）」という着想に至れる子も増えるのではないでしょうか。この問題でも階乗の増大スピードを掴んでいることが答えの予測に役立つように、数の大きさの感覚には鋭くなっておきたいところです。ちなみに別解にあげた「$${a!}$$、$${c!}$$、$${b!}$$ がこの順に等差数列をなす」という見方ができれば、大小関係として $${a \leqq c \leqq b}$$ になるんだろうなと予想するのは易しいですね。

　また、「一般性を失わない」というのは「並べ替えたり回転したりすることでいつでも一つの状況に帰着できる」ということを意味します。勝手に制約をつけて特殊な状況だけを考えているように見えるものの、実は本質的な部分を抜き出せているため一般的な状況まで考察できている、ということですね。ここに書いたことを答案に書くわけにはいかず「一般性を失わない」で十分に伝わりはしますが、指導者が教えるときにはきちんと補足するべきだと思います。

　本問では、⑴と⑵により「不等式（大小関係）を使って範囲を絞る」という典型的な手法に誘導する、という流れになっていて、それでいて⑶では対称性に注目して自力で大小関係を導入することが求められます。整数問題に関する総合的な力が問われていて、非常にいい問題だと感じました。今後いろんな問題集に載るでしょう。

第４問　地道に手を動かせば解けるがどこまで書くべきか悩む。

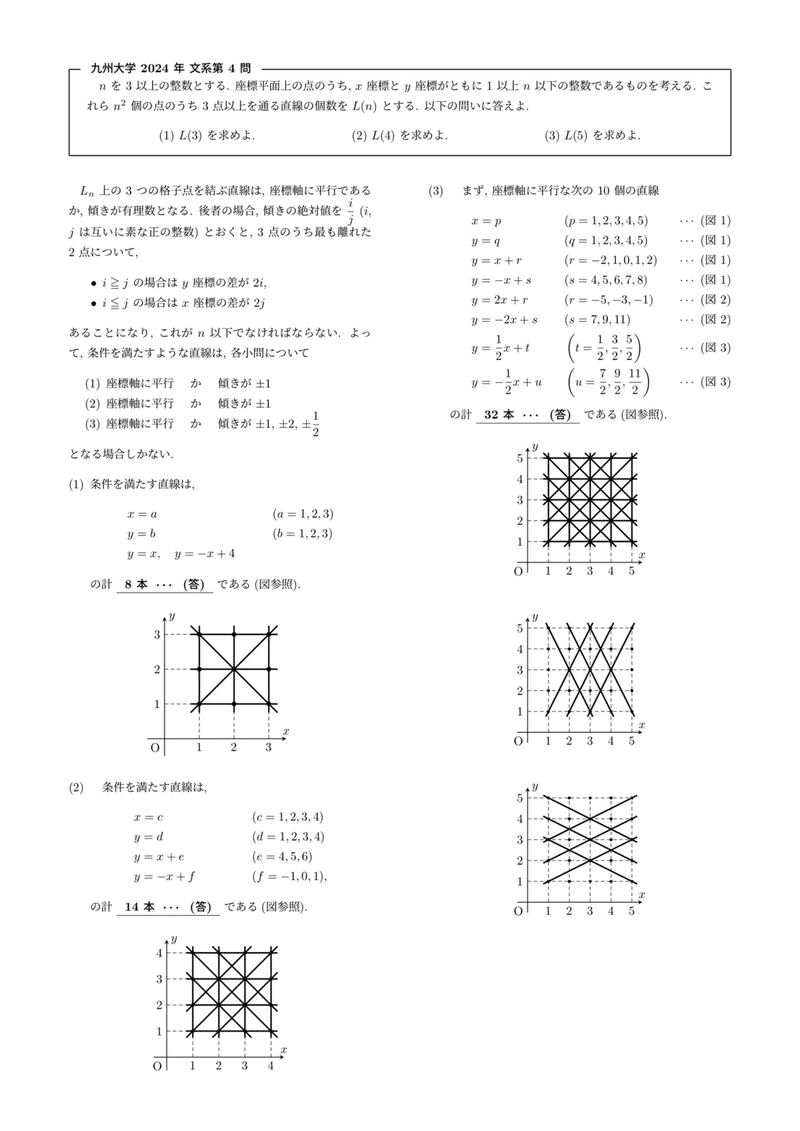
　第１問から第３問は、解法次第では相当見通しよく解ける問題だったのに対して、本問は「上手い解法」が存在せずただ地道に数えるしかないと思われます。条件を満たす直線を実際にグラフに描いてみるのが一番手っ取り早いですが、問題は「それ以外にはありません」というところをどう説明するかです。おそらく図をちゃんと描くだけでも満点がもらえるのではないか、と思われますが「個数を求めよ」には「過不足なく求めよ」という意味も含まれていますので、そのあたりの論証がカギになると考えました。

　私は、条件を満たす直線の傾きが有理数の場合に着目し、最も離れた２点の $${x}$$ 座標（あるいは $${y}$$ 座標）の差を $${n}$$ 以下に収める必要がある、という説明を補足し、傾きが取り得る範囲を絞り込んでからぜんぶ描く、という方法を選びました。切片をシラミツブシに書くことで本数を数えやすくなりますね。

最後に

　今年度の九州大学の文系数学は、標準的な受験勉強をしていればいずれも完答が狙える問題が並び、それでいて地道に手を動かすことが功を奏する良問ばかりでした。入試としても程よく差がつけられるでしょうし、演習効果もかなり高いと思います。次は

• 北海道大学　文系

• 東北大学　　文系

• 京都大学　　文系

あたりの問題に取り組もうと思いますが、今後は週一ペースでの更新はできないかもしれません。今月中に一つ出せればいいなと思います。よろしくどーぞ！