統計準一級　第16章　重回帰分析　解説

重回帰分析の基礎(p125-126)

最小2乗推定量は単回帰と同様に平均2乗誤差を損失関数として微分から最小値を求めることができる。

各誤差の解説 (p126-127)

全変動は回帰変動(淡い青)と残差変動(縞青)に分けられる

$$
y = \beta_0 + \beta_1x_1 + \cdot \cdot \cdot + \beta_dx_d + \epsilon
$$

において各誤差の性質を下記に述べていく。

SST (Sum of Squares Total)

$$
SS_{T} = {\Sigma_{i=1}^{n}(y_i - \bar{y})^2}\\
n-1       d.o.f
$$

これは全変動と呼ばれる
目的変数がデータの平均からどれくらい差があるかを表す
また、n-1で割るとyの分散になるのでデータがそもそもどれくらい散らばっているかを表す指標

SSR (Sum of Squares Regression)

$$
SS_{R} = \Sigma_{i=1}^{n}(f(x_i)(= \hat{y_i})  - \bar{y})^2\\
d       d.o.f
$$

これは回帰変動と呼ばれる
$${x_i}$$から回帰モデルによって推定された値がデータの平均からどれくらい差があるかを表す
全変動の回帰verとイメージすればおけ

SSE (Sum of Squares Error)

$$
SS_{E} = \Sigma_{i=1}^{n}( y_i - f(x_i)(= \hat{y_i}) )^2\\
n-1-d       d.o.f
$$

これは残差変動と呼ばれる
$${\hat{y_i}}$$ は$${x_i}$$から回帰モデルによって推定された値なので$${y_i - \hat{y_i}}$$は$${y_i(=f(x_i)}$$の回帰で説明されなかった部分でこれを残差(residuals)という。
残差が大きいほど回帰モデルでは説明できない誤差が大きいということなので、モデルの精度が悪いということになる。

自由度調整済み決定係数　(p127-p128)

重回帰モデルでは下記の等式が成り立つ
SST（全変動） = SSR（回帰変動）+ SSE（誤差変動）

重回帰の検定ではモデルによって説明できる誤差（SSR）を大きくして
ランダムな誤差（SSE）を小さくなるようにする。
つまり誤差を出来るだけ下図の緑字のような説明可能に出来るだけしたい

従って下記の式が指標として導出できる
SSEの割合が小さいほど決定係数が大きくなりデータのあてはまりが良いということになる
また各項で自由度を調整し正規化しているに注意する

$$
R^2(自由度調整済み決定係数) = 1 - \frac{SSE}{SST} = 1 - \frac{\Sigma_{i=1}^{n}\frac{( y_i - \hat{y_i} )^2}{n-1-d}}{\Sigma_{i=1}^{n}\frac{(y_i - \bar{y})^2}{n-1}}
$$

https://vitalflux.com/linear-regression-explained-python-sklearn-examples/

有意性検定　（p130-131）

今度は下記について考えれば、これは自由度（q, n-d-1）のF分布を表す

$$
T = \frac{SSR}{SSE} = \frac{\Sigma_{i=1}^{n}(\frac{f(x_i)(= \hat{y_i})  - \bar{y}}{q})^2}{\Sigma_{i=1}^{n}\frac{( y_i - \hat{y_i} )^2}{n-1-d}}\\
where  q < d + 1 
$$

正則化　（p131-132）

 $${(X^TX)^{-1}}$$ が存在しない時に正則化項を追加すると
例えば下記のように回帰係数の推定量が算出される

正則化で有名なのは主に3種類存在し、Ridge回帰Lasso回帰Elastic-Net回帰と呼ばれている。
RidgeとLassoの特徴を持っているのがElastic-Net回帰である。

https://benrishi-ai.com/regularization02/

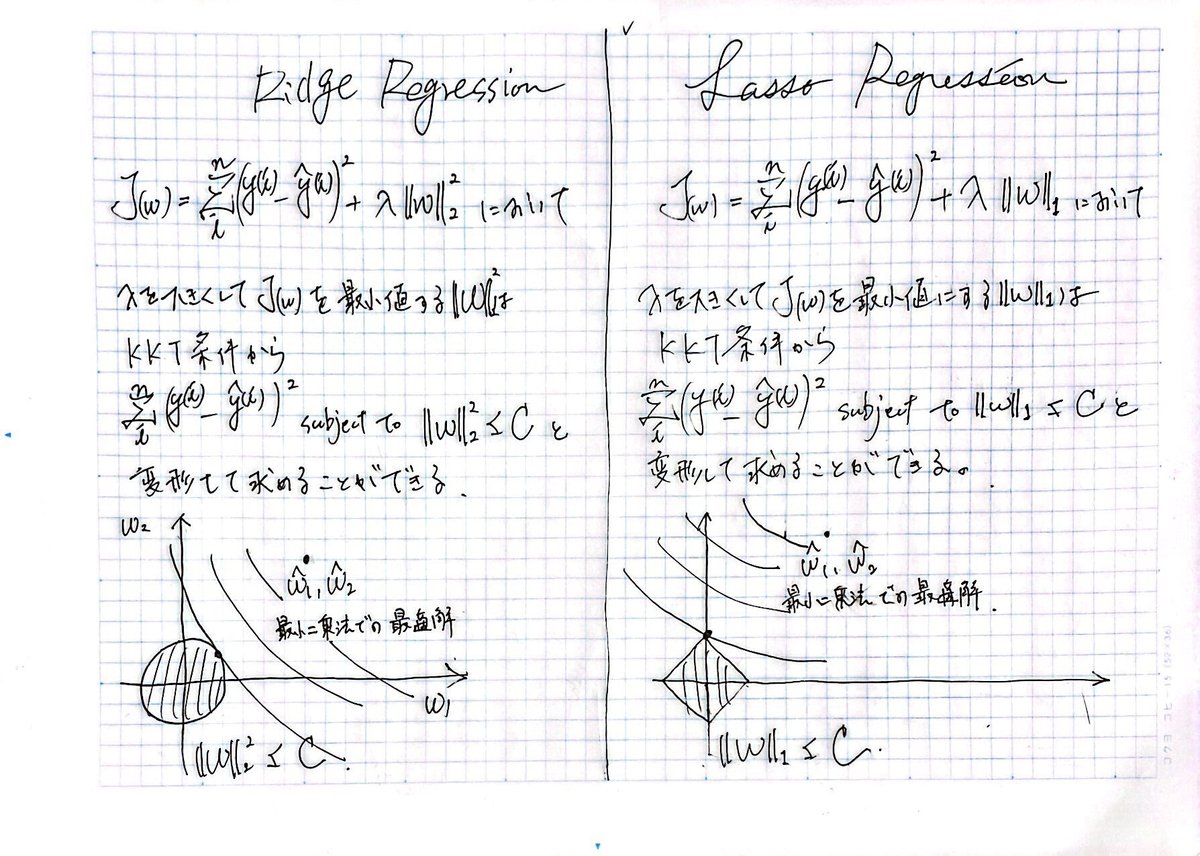
Ridge回帰では下記の図のように特徴量が0になることは極めて稀だが
Lasso回帰ではほぼいずれかの特徴量が0になるスパース解が得られる。

参考文献