
統計準1級 第8章 統計的推定の基礎 解説
この章の目的 : 何が優れた推定量なのかを学ぶ
例えば推定量の1つに最尤推定量があるが
「なんで最尤推定量を用いるのか」
そもそも推定量について考えたことはあんまりないと思う
実際問題推定量なんてなんでもいいのだが
基準をみたして優れている推定量を一般に用いることが多く
最尤推定量やベイズ推定量などが挙げられる
なので今回は優れた推定量である最尤推定量について学習したあとに
推定量の様々な性質について触れていく
最初に簡単な用語の導入をする
推定値と推定量
標本$${X_1, X_2, \cdots, X_n}$$から
例えば母平均を推定しようとして、標本平均を用いるとする
このとき$${\bar{X} = \frac{1}{n} \sum_{i} X_i}$$は推定量といい
この推定量に観測値を入れて
$${\bar{x} = 2.5}$$みたいに実際の値になったものを推定値という
基本的に統計的推定は
標本の観測値$${x_1, x_2, \cdots, x_n}$$から適切な優れた推定量を用いて
確率分布の未知のパラメーター(正規分布だったら平均と分散)
を推定していく
次に代表的な推定量である最尤推定量を紹介する
最尤推定量
最尤推定量の概要と計算
与えられた観測データから「尤(もっと)もらしい」パラメータ値を推定するための一般的な手法の1つ
尤度に関して詳しくは下記を参照
最尤推定法は、以下の手順で行う
尤度関数の定義:観測データの同時確率分布を尤度関数として定義する
対数尤度関数の最大化:尤度関数が複雑な場合、対数をとって積を和に変換し、対数尤度関数を最大化する
パラメータの推定:最大化された対数尤度関数におけるパラメータの値が、最尤推定量として得られる
なんかよくわからないと思うので
ポアソン分布を例にする
まず対数尤度関数を定義して

対数尤度関数の最大値を求めて

標本データからパラメーターを推定する
最尤推定量が求まる(今回は標本平均)

十分統計量
十分統計量とは、与えられたデータから推定するパラメータに関する情報を完全に含んでいる統計量のこと
なので十分統計量だけを知っていれば、
他のデータの詳細情報は不要で、パラメータを推定できる状態になれる
※ 尤度比検定など必ずしもパラメーターの推定だけに用いるだけではないので「推定量」ではなく「統計量」となっている
十分統計量かどうかを確かめるには、
一般的には条件つき確率を計算する必要があるが
条件つき確率の計算は煩雑になることが多いため
十分統計量の必要十分条件である下記の
フィッシャー・ネイマンの分解定理が利用されることが多い

最尤推定量は十分統計量のみの関数
統計検定準1級のワークブックによると
「(中略)対数尤度関数の$${\theta}$$を含む項は$${T(X)}$$にのみ依存するため、最尤推定量は十分統計量のみの関数となることがわかる」
とかいてあるが一体どういうことだろうか
実際にフィッシャー・ネイマンの分解定理を用いて
最尤推定量を計算するとわかる
十分統計量$${T(X)}$$が存在するとき
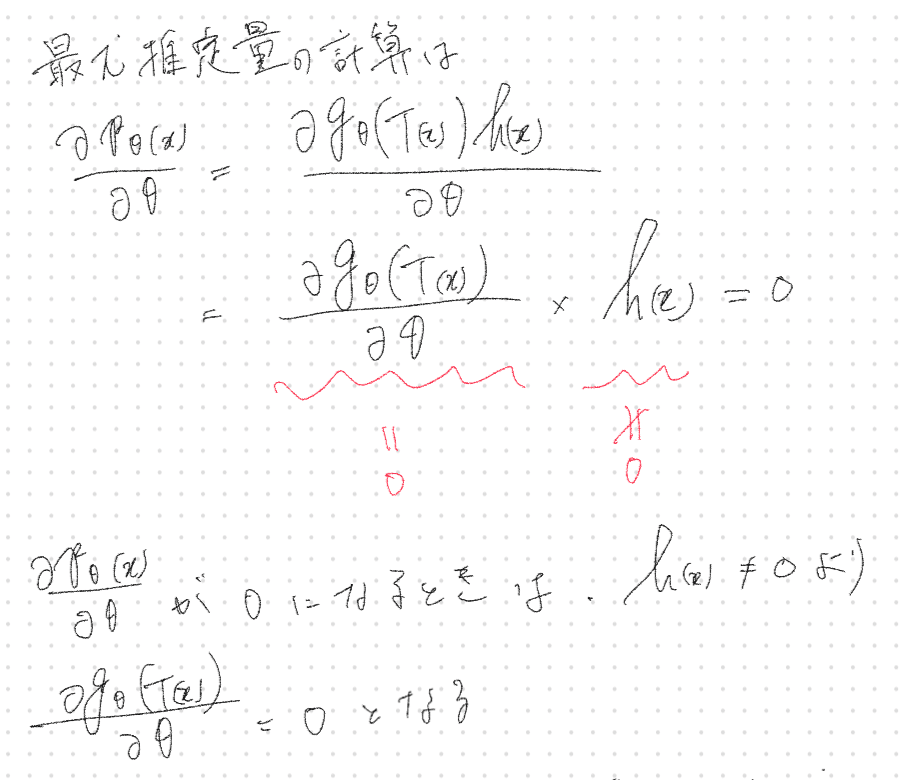
よって得られる最尤推定量は
十分統計量$${T(X)}$$の関数となる
また最尤推定量は十分統計量のみの関数となるので
データのパラメーターの推定が十分にできる推定量だということもわかる
点推定の性質
不偏推定量
パラメーターの期待値が母集団の真の値と合致するとき$${E_{\theta}[\hat{\theta}] = \theta }$$となる$${\hat{\theta}}$$を不偏推定量という
不偏推定量は統計的推定で扱われる推定量で、母集団の未知パラメーターを推測するために使われる
このパラメーターと推定値の誤差が小さいほど、良い推定と言えるので以下のようなパラメーターと推定値の平均二乗誤差を考える
$$
\begin{aligned}
& E_{\theta}[(\hat{\theta} - \theta)^2] \\{}\\
& = E_{\theta}[((E_{\theta}[\hat{\theta}] - \theta) +(\hat{\theta} - E_{\theta}[\hat{\theta}]))^2] \\{}\\
& = (E_{\theta}[\hat{\theta}] - \theta)^2 + Var[\hat{\theta}]
\end{aligned}
$$
ここの第1項$${(E_{\theta}[\hat{\theta}] - \theta)^2}$$は実測値と推定値平均との差(→バイアス項)と呼ばれる
ここのバイアス項を0にする$${E_{\theta}[\hat{\theta}] = \theta }$$となる$${\hat{\theta}}$$を不偏推定量という
不偏推定量の具体例は下記を参照されたい
有効推定量
不偏推定量は
平均二乗誤差の第1項$${(E_{\theta}[\hat{\theta}] - \theta)^2}$$
を0にするものだった
$$
\begin{aligned}
& E_{\theta}[(\hat{\theta} - \theta)^2] \\{}\\
& = E_{\theta}[((E_{\theta}[\hat{\theta}] - \theta) +(\hat{\theta} - E_{\theta}[\hat{\theta}]))^2] \\{}\\
& = (E_{\theta}[\hat{\theta}] - \theta)^2 + Var[\hat{\theta}]
\end{aligned}
$$
有効推定量は
さらにこの誤差を少なくしようとする推定量で
第1項を0にした上で下記の第2項$${Var[\hat{\theta}]}$$
を最小にする推定量である
ではどうやって最小かどうか確かめるかというと
クラメール・ラオの不等式を用いる
$$
V_{\theta}[\hat{\theta}] \geq J_{n}(\theta)^{-1}
$$
ここで$${X_n}$$が独立同一分布に従うとき
フィッシャー情報量はサンプルサイズに比例するので
$$
J_{n}(\theta) = nJ_1(\theta)
$$
となるので
最小値は以下の不等式から確認することができる
$$
nV_{\theta}[\hat{\theta}] \geq J_{1}(\theta)^{-1}
$$
有効推定量の具体例と付随する漸近有効性という概念は下記を参考にされたい
一致推定量
標本のサンプル数 $${n}$$を増やして以下のような不等式が成立するものを一致推定量という
基本はチェビシェフの不等式を活用することが多い
ちなみにチェビシェフの不等式とは
確率変数$${X}$$の期待値を$${m}$$, 標準偏差を$${s}$$とすると任意の正の数$${a}$$について
$$
\forall a > 0, P(| \hat{X} - m | \geq as ) \leq \frac{1}{a^2}
$$
一致推定量の具体例は下記を参照されたい
漸近的な性質
標本が十分に大きくサンプル数が$${n \rightarrow \infty}$$のとき
推定量がイケてるかどうか判断する理
漸近有効性
漸近有効性とは、
$${n \rightarrow \infty}$$のとき
推定量が他の推定量よりも情報を効果的に利用して
パラメータを推定することができるという性質のことをさす
正確に言えば
任意の推定量を$${n \rightarrow \infty}$$して
振る舞う分布(漸近分布という)の分散(漸近分散という)
が最小値をとる(クラーメル・ラオの不等式から判断)
とき推定量は漸近有効性をもつ
漸近有効性の具体例は下記を参照されたい
漸近正規性
最尤推定量は漸近正規性を示すのだが、証明は難しい
最尤推定量の1回微分を、テイラー展開したあとに
式変形して各項の分布収束を見る必要がある
下記の動画に証明があるので、気になる方は参照されたい
https://www.youtube.com/watch?v=DSEFA5RBzKo&t=404s
なので今回は
最尤推定量は漸近正規性を示すだけ押さえておけばいい
推定量の補正
不偏推定量ではなく推定量にバイアスがある場合はどうしたら良いか
得られている標本の値を再利用して補正するジャックナイフ法がある
ジャックナイフ法は簡単にいうと
標本の値を1つ削った標本平均をサンプルの数だけ作り
再度標本平均を作成し補正するという流れになる

詳しくは下記を参照にされたい
この記事が気に入ったらサポートをしてみませんか?
