【日本語訳】YieldSpace: An Automated Liquidity Provider for Fixed Yield Tokens

2022年8月7日 07:26

この記事は、Yield Protocol、ParagigmのDanDan Robinsonらによって書かれた論文「YieldSpace: An Automated Liquidity Provider for Fixed Yield Tokens」の日本語訳記事になります。

Allan Niemerg allan@yield.is
Dan Robinson dan@paradigm.xyz
Lev Livnev lev@dapp.org
和訳：@osoeysk

イーサリアムプロトコルは、イーサリアムブロックチェーンでの固定金利の借り入れと金利の発見を可能にするゼロクーポン債に似たファンジブルトークンであるfyTokensの概念を導入しました。 fyTokensは、UniswapのようなAMMを含め、どこでも取引できますが、これらのシステムで使用される式はfyTokens用に最適化されていないため、満期の近いfyTokensのトレーダーにとっては価格への影響と手数料が高くなり、流動性プロバイダーの裁定取引による予測可能な損失が発生します。このペーパーでは、AMMの新しい公式である「constant power sum invariant(一定のべき和不変)」を紹介します。これは、満期までの時間の概念を組み込み、流動性プロバイダーがその準備金の特定比率に対して価格ではなく一定の金利を提供することを保証します。また、このペーパーでは目的のプロパティを持つプールの不変量を導出するために使用できる、一般的に有用な方法論を紹介します。

1 Introduction

Yield Protocolの論文で、著者はfyTokensを紹介しました。これは一定の満期日にターゲット資産と交換できる合成トークンです。fyTokenの価格は満期前に自由に変動し、その価格は特定の金利を意味します。 fyTokenが満期になるまで、その資産を借りたり貸したりします。 fyTokensは、ユニスワップのようなプールされた流動性供給のための既存のプロトコルを含め、ERC20の取引をサポートする場所ならどこでも取引できます。それ自体がERC20であるターゲットアセットを持つfyTokenの場合、トレード対象となる最も明白なペアは、そのターゲットアセットです。このホワイトペーパーでは、Yield Protocol [2]を使用して実装されている最初のトークンであるfyDAIに焦点を当てます（ただし、説明されている設計は他のfyTokenでも機能する可能性があります）。 fyDAIは、DAIをターゲットアセットとするfyTokenです。 fyDAIは、満期時に1対1でDAIと引き換えることができます。満期から遠く離れているとき、fyDAIはさまざまな価格で取引することができます。 fyDAIは、満期に近づくと、DAIとの償還が差し迫っているため、金利に関係なく1DAI近くで取引される可能性があります。イーサリアムでトークンを交換するための最も一般的なプロトコルは、プールされた流動性を使用し、数式に基づいて価格を自動的に設定します。これらの式は2つの資産の準備金間の固定関係を指定する不変量として表されます。たとえば、ユニスワップは一定の積の不変量 x・y = kを使用します。ここで、xとyは2つの資産のプールの準備金です。これらの不変条件はプールの準備金が常に従うことを保証するプロパティに基づいて選択できます。既存のAMMが使用する不変条件は、fyToken用に最適化されていません。 Uniswap[3]およびBalancer[4]で使用される「constant product invariant」の公式は、満期に近いfyTokenの場合、資本効率が悪い可能性があります。mStable [5]で使用され「constant sum formula」の式は、価格発見を完全に放棄するため、取引を思いとどまらせる可能性があります（fyDAIの価格は時間とともに変化し、ほとんどの場合は満期前に1 DAI未満になるため）。 Curveのようなハイブリッド式は、これら2つのモデル間の妥協点ですが、満期までの時間に基づいてパラメーターを調整する方法がありません。実際、これらの式は、リザーブ（およびその他の定数パラメーター）のピュアな関数であり、いずれも時間の概念を組み込んでいません。所定の準備金残高について、提供される価格は時間の経過とともに一定のままです。したがって、これらのプールは、金利が変わらない場合でも、満期が近づき、fyDAIの価格が1に近づくにつれて、裁定取引による予測可能な損失に苦しむことになります。このホワイトペーパーでは、fyTokenとそのターゲットトークン間のマーケットメイクに最適化された新しい不変条件である「constant power sum formula」を紹介します。

yはfyToken（fyDAIなど）のリザーブを表し、xはターゲットトークン（DAIなど）のリザーブを表します。 tは満期までの時間を表します。 tの単位は0≤t<1になるように正規化されていると仮定します。fyDAIの最初の実装では、満期から4年でt=1になるように単位が正規化されます。この曲線は、「constant sum formula」と「constant product formula」のハイブリッドによく似ています。 t = 0の場合、式は一定の合計式x + y = kになり、一定の価格1で流動性が提供されます。tが1に近づくにつれて制限を適用すると、式は一定の積の式 x・y= kに近似します。（アペンディクスDで証明されているように）

この計算式は、「Price Space」ではなく、「Yield Space」の価格計算式として扱うことができます。以下で説明するように、この式には、プールによっていつでも提供されるfyDAIのマージナルインタレストレートが、DAIの準備金に対するfyDAIの準備金の比率（マイナス1）に等しいという独自の特性があります。

*rは請求された時に支払い準備があることを保証する金利(マージナルインタレストレート)

たとえば、fyDAIの準備金が110、DAIの準備金が100の場合、プールによって提供されるマージナルインタレストレートは10％の金利を意味します。この公式は「準備金が変わらない場合にプールによって提供されるマージナルインタレストレートが時間の経過とともに変化しない」ことを保証します。
言い換えると、「プールの目標fyDAI割り当ては、fyDAIの現在の取引価格によって暗示される金利とまったく同じ金利で時間の経過とともに増加」します。これは裁定取引による損失を防止するものではありませんが、裁定取引の機会は金利が変化した場合にのみ発生するはずであることを意味します。「constant power sum invariant」は、fyDAIのためのAMMの一部として実装されています：YieldSpace。 YieldSpaceはYieldチームによって実装されましたが、コアのfyDAIコントラクトから切り離されており、個別にアップグレードできます。
　セクション2では、不変量ベースの流動性供給式に関するいくつかの先行研究について説明します。セクション3では、これらのプロパティを微分方程式として表現し、それらを解くことにより、目的のプロパティを持つ新しい不変量を導出するための一般的に適用可能な方法論について説明します。セクション4は、「constant power sum invariant」を導出する方法を示しています。セクション5では、金利と満期までの時間を考慮した方法で、この公式に手数料を組み込む方法について説明します。最後に、セクション6では、流動性トークンがどのように機能するかを説明し、プールの資本効率を改善する最適化方法を紹介します。

2 Invariant-based liquidity provision formulas

Uniswap、Curve、Balancer、Bancorなど、イーサリアムでトークンを交換するための一般的なプロトコルのほとんどは、いくつかの不変条件を利用しています。

これは、プールのある資産yと別の資産の準備金xの準備金間の関係から表現できるAMMのアルゴリズムです（手数料を無視）。

2.1 Constant sum formulas

おそらく最も単純なAMMである「constant sum formula(x+y=k)」は、常に同じ価格で資産を取引します。

「constant sum formula(x+y=k)」は、常にまったく同じ相対価格で取引されるトークン用に最適化されています。トークンの相対価格が予想価格と異なる場合、「constant sum formula」を使用するプールは価値の低いトークンのみを保持し、比較的少ないボリュームで取引をすることになります。（AMMは価値の高い方のトークンの比率が少なくなるため、市場価格を超えた価値の低い方のトークンを提供することになります）。fyDAIは生涯にわたってさまざまな価格で取引できるので、「constant sum formula」は、fyDAIがすでに満期を迎えてない限り適切ではありません。（したがって、DAIと同等に取引する必要があります）。

2.2 Constant product formulas

「constant product formula(xy=k)」の公式は、GnosisのAlan Luによって最も認識可能な形式で最初に提案されました[8]：

この公式は、ユニスワッププロトコルの一部としてイーサリアムに実装されました[3]。この式は、プロトコルによって提供される現在の価格で、各トークンのプールのリザーブの値が等しいという特性を維持します。

Luはまた、3つ以上のアセット（x、y、z…)、およびカスタムのプールの重み付け（wx、wy、wz…）をサポートするバージョンの「constant product formula」を提案しました。：

この式は、バランサープロトコルの一部としてイーサリアムに実装されました[4]。「constant product formula」の公式は、満期が非常に長いfyTokenに適している可能性があります。ただし、満期が短いfyToken（1年以内に満期するものなど）には適していません。まず、fyTokenが満期に近づくにつれて、その価格はターゲットトークンと同等になる傾向があります。「constant product formula」の公式は、全価格スペクトルに沿った価格のために流動性を確保し、特定の価格の周りに比較的少量の流動性を残します。これは、大規模な取引が、獲得または支払われる金利に大きな影響を与える可能性があることを意味します。第二に、これらの公式によって請求される取引手数料は、満期までの時間や現在の金利に関係なく、取引された金額に比例します。 fyTokenが満期に非常に近い場合、わずかな手数料でも大きな金利スプレッドが発生する可能性があります。たとえば、fyTokenが満期まで1か月、年利が5％の場合、0.3％の手数料は(r=x/y - 1より)、借入金利が（1 / 0.95・0.997 ^ 12）-1 = 9.1％であり、貸付金利は（0.997 ^ 12 / 0.95）− 1 = 1.01％であることを意味します。 - 8％以上のスプレッド。最後に、これらの公式は満期までの時間を考慮していないため、fyTokensが満期に近づき、トレーダーが価格を同等に押し上げる裁定取引を実行すると、流動性プロバイダーは予測可能な「インパーマネントロス」の影響を受けます。「constant power sum formula」では、インパーマネントロスを排除することはできませんが、価格が変化するたびにではなく、金利が変化したときにのみプールを裁定取引にさらすことで、損失を減らすことができます。

2.3 Other invariants

Curveは、価格が一定の価格で取引されると予想される（ただし必ずしも正確に取引されるとは限らない）資産に対してカスタム式を実装します。 CurveのStableSwapペーパー[9]に示されている式は、2トークンの場合、次のように書き直すことができます（χは増幅係数）読み方：カイ

χ=0の場合、この曲線は「constant product formula」の式に還元されることに注意してください。 χが無限大に近づくと、曲線は「constant sum formula」の式に近づきます。 Curveの式は、「constant sum formula」または「constant product formula」よりも柔軟性がありますが、満期までの時間の関数としてこの増幅率χを計算する方法はありません。その結果、プールによって提供される金利が一定に保たれること、または時間の経過とともにプールの流動性が金利の範囲全体でバランスが保たれることを保証するものではありません。

3 How to build your own invariant

例えばいくつかの特性を満たす流動性供給式を考え出したいとします。「2つの資産の50対50ポートフォリオを維持する公式」を探しているとします。この特性を前提として、準備金xとyの間の不変の関係で表される、それを満たす流動性供給式をどのように考え出すことができますか？まず、これらすべての曲線に関する重要な事実を観察しましょう。アリスがx資産の一部をプールに売却した場合、プールのxの準備金はその量だけ増加し（dxと呼びます）、プールのyリザーブはある程度減少します（yが下がっているため、 y、dyは負であるため、-dyは送信されるyのアセットの量です）。比率-dy/dxは、アリスがxの資産を売却した価格を表します。非常に小さいdxのこの比率 - lim dx→0(−dy/dx) - その時点での負の導関数は、その時点でのコントラクトによって提供できる限界の価格を示します。

つまり、価格、準備金、およびその他の量（時間など）の間の何らかの関係を満たす式が必要な場合は、そのプロパティを微分方程式として書き直すことで、それを満たす不変量を見つけることができます。（xstartとystartを指定することで、初期値問題に変えることができます。）たとえば、常に1の固定価格で取引することを提案する式が必要だとします。これは自明な微分方程式として表すことができます。

アペンディクスAに示すように、これに対する解決策は「constant sum formula」の式です。別の例として、コントラクトによって提示された現在の価格で、プールの2つの資産の準備金の価値が等しいというプロパティを与える式が必要だとします。 pxはyトークンに関するxトークンの価格であるため、この望ましい関係はpx・x=yとして表すことができます。 px = − dy/dxなので、このプロパティを次のように書き換えることができます。：

アペンディクスBに示すように、この微分方程式の解は、「constant product formula」の公式x・y=kです。同じプロセスを使用して、1以外の価格でトークンを提供する「constant sum formula」のバージョン、および2つ以上のトークンまたは50/50以外の重みをサポートする「constant product formula」式のバージョンを見つけることができます。すべての関係が解くことのできる微分方程式を与えるわけではありませんが、これは、望ましい特性を持つ新しい式を発見するための強力なツールになるのに十分に機能します。

4 The constant power sum formula

「Price Space」ではなく「Yield Space」で機能するAMMを構築したいと考えています。具体的には、価格ではなく金利を準備金の関数にする必要があります。この関数が何であるかについては、多くの可能な選択肢があります。金利がfyDAI準備金（y）とDAI準備金（x）の比率から1を引いたものである式を見つけることにしました。

この選択の動機は、前述のように、準備金間の比率を価格として使用する「constant product formula」の公式に類似しています。また、fyDAIの準備金が増えると金利が上がり、DAIの準備金が増えると金利が下がるという望ましい特性が見られます。最後に、このプロパティにより、解のある微分方程式が得られ、コントラクトに効率的に実装できる閉形式の不変量を見つけることができます。
　Yield Spaceの論文[1]で説明されているように、fyDAIの金利は、fyDAIの現在の価格pと、満期までの時間tの関数として計算できます。

たとえば、今日から6か月で期限切れになる1fyDAIが現在0.5DAIの価値がある場合（つまり、fyDAI、pでのDAI価格は2）、これは年利が2^1/0.5 − 1 = 300％であることを意味します。
　上記の2つの方程式を単純化すると、この方程式が得られます。

不変量ベースの流動性供給式では、曲線に沿った任意時点での価格は、その時点での導関数の負に等しくなります。

したがって、金利が常に準備金の比率から1を引いたものに等しい曲線を見つけると、次の微分方程式を解くことができます。

アペンディクスCに示すように、この微分方程式の解は次の方程式です。

4.1 Properties

セクション1で説明し、アペンディクスDに示すように、「constant power sum formula」は、lim t→1での「constant product formula」からt=0での「constant sum formula」へと徐々に進化します。

不変のxstart1-t +ystart1-tは、tの現在の値、およびxとyの現在の準備金に基づいて、取引ごとに再計算されます。これは、現在の準備金を表す時点を中心に曲線が「ピボット」することを意味します。上のグラフは、レートが0％の場合に曲線がどのように変化するかを示しています。レートが100％の場合（プールにDAIの2倍のfyDAIがあることを意味します）、曲線は次のようになります。

与えられたxstart、ystart、およびtの（fyDAIに関するDAIの）限界価格は、次の式で与えられます。x1-t + y1-t =xstart1-t +ystart1-t = invariant

価格曲線は、満期が近づくにつれて徐々にフラットになります。

しかし、価格ではなく金利を見るとどうなるでしょうか。限界金利の式を思い出してください。

金利のグラフは、満期が近づくにつれて最小限にしか変化しません。

言い換えれば、この公式は、コントラクトの存続期間にわたって比較的一貫した範囲の金利にわたって流動性を提供します。金利が0％の場合、コントラクトの少なくとも半分のDAIの流動性は、100％を超える金利で流動性を提供するためにリザーブされていることに注意してください。これが年利を表す場合、それは比較的ありそうもないケースのために確保された多くの流動性になります。プール内の有用な流動性を最大化するために、契約はtの単位を正規化して4年でt = 1にします。これは、式y/xで与えられる利率が年利ではなく4年利であることを意味します。さらに重要なことに、金利が0％の場合、プールのfyDAIはすべて、負の金利で流動性を提供するために予約されています。つまり、無駄になります（fyDAIは1DAIより高い価格で取引されるべきではないため）。セクション6.3では、この問題とその軽減策について説明します。

5 Fees

流動性プロバイダーにトークンをプールに預けるようにインセンティブを与えるために、すべての取引に手数料を請求するのが通例です。

「constant power sum formula」の公式は、金利が上がるとfyDAIを購入し（そしてそれに利息を稼ぎ）、金利が下がるとそれを売るので、手数料を考慮する前でも、プールがfyDAIとDAIの両方の収益を上回る可能性があります。 https://medium.com/sensefinance/space-pool-lp-returns-ae1be073b4a5（対照的に、時間の概念を組み込まない静的な不変量は、手数料を差し引く前に、その構成資産の少なくとも1つを常にアンダーパフォームします。）それでも、流動性にさらに報いるために、プロトコルに手数料を組み込むことができます。他のプロトコルでは通常、料金は販売された金額に比例して請求されます。たとえば、Uniswap v2では、送信金額が計算される前に、コントラクトに送信されたトークンの0.3％の料金が請求されます。ただし、fyTokenが満期に近づくと、わずかな手数料でも金利の面で広範囲に影響が広がる可能性があります。価格と同様に、手数料は「Price Space」ではなく「Yield Space」で計算する必要があります。つまり、価格ではなく、金利に比例したスプレッドを課す必要があります。たとえば、手数料が調整された式では、fyDAIの購入者は、セクション4で導出された手数料を考慮しない式よりも低い金利（より高い価格を支払うことに相当）を受け取る必要があります。金利を下方修正する最も簡単な方法は、金利を（1を引く前に）一定のg(<1 )の累乗に上げることであると考えています。

たとえば、プールのfyDAI残高が110、DAI残高が100、gが0.95の場合、未調整の数式は110/100 − 1 = 10％の限界金利になります。調整された式は、110/100 ^ 0.95 −1≈9.47％の限界金利を与えます。請求される手数料（0.5％）は、現在の金利の約5％であることに注意してください。金利が比較的小さく、g <1の場合、二項近似は（1 + r）^g≈1+grであることを示しています。使用される実際の不変条件は、取引の方向によって異なります。トレーダーがコントラクトからfyDAIを買う場合、上記の不変条件を1未満のgで使用して、金利を下げます（したがって、fyDAIに支払われる価格を上げます）。x1-gt+y1-gt= invariant ユーザーがfyDAIをコントラクトで売る場合、代わりに金利が1/gの累乗に引き上げられ、ユーザーはより高い金利を支払うことになります（つまり、販売しているfyDAIの価格が低くなります）。x1-t/g+y1-t/g= invariant. 上記の例では、借り手（fyDAIをプールに売っている人）の限界金利は110/100 ^1/0.95 −1≈10.55％になります。上記の手数料方程式を微分方程式に変換し、セクション4とアペンディクスCで使用したのと基本的に同じ手順を使用して解くことにより、次の不変量を導き出します（fyDAIを販売するときはgtをt/gに置き換えます）。

この手数料計算式のもう1つの便利な特性は、取引を複数の部分に分割しても、より高いまたはより低い手数料を支払うことにはならないことです（modulo precision error）。送信されたトークンのパーセンテージとして料金が請求される場合（Uniswapやその他のほとんどの場合と同様）、このプロパティは保持されないためため、取引を複数の部分に分割するユーザーは、それらを組み合わせた場合よりも高い料金を支払います。これにより料金を分析しやすくすることができます。

6 Liquidity tokens

ユニスワップと同様に、すでにプールにある準備金に比例してDAIとfyDAIを提供することにより、誰でもプールに流動性を追加できます。それらが流動性を提供するとき、それらは流動性提供されたトークンの比例したシェアが割り当てられます。

6.1 Initialization

プールは、DAIとfyDAIの等しい準備金で初期化する必要があります。これは、価格が1、金利が0％であることを意味します。異なる金利でプールを初期化するには、プールを0％で初期化してから、分割できなくなるまで取引して目的の金利にプッシュします。最初に作成されたプールのトークンの数は、供給されたDAIの量と同じです。流動性プールのトークンがこのように初期化されると、次の不変条件は、コントラクトの状態変化に伴って減少しないことが保証されます（アペンディクスEに示されているように）：

プールが取引からの手数料とそのfyDAI保有からの利息を蓄積するにつれて、この不変量の価値は上昇します。

6.2 Minting and burning

流動性トークンのミントとバーンは、ユニスワップやその他のプールされた流動性プロビジョニングプロトコルと同様に機能します。新しい流動性プロバイダーがプールに入ると、それらはすでにコントラクトの準備金にあるDAIとfyDAIに比例してDAIとfyDAIを預け入れ、プール内の総供給量に同じ割合で新しく作成された流動性供給トークンを受け取ります。(depositトークン量の変化率とシェアの変化率は比例)

6.3 Capital efficiency

通常の状況では、1fyDAIが1DAIよりも高い価格（マイナス金利に相当）で普通は取引されることはありません。コアのfyDAIプロトコルでは、常に1つのDAI担保を預けることで1つのfyDAIを作成できます（清算のリスクはありません）。したがって、1DAIを超える価格でプールからfyDAIを購入する理由はありません。さらに、上記の式は、fyDAIの価格が1を超えないことを前提としています。その結果、プールは各取引の最後にfyDAIの価格が1 DAIを超えていないこと、または同等に、fyDAIのリザーブがDAIのリザーブよりも多いことを確認します。この要件の結果として、プールで使われないfyDAIリザーブの一部があります。

たとえばプールが最初に初期化されたとき、fyDAIリザーブとDAIリザーブは等しいため、プールに残っているfyDAIを売ることができません。いつでもアクセスできないfyDAIの量は、1対1の比率で即時取引があった場合にコントラクトに含まれるfyDAIの量を計算することによって与えられます。この解決策は次の式です。

これらの超過準備金の一部を「Virtual」にし、流動性プロバイダーにそれらを提供させないことにより、プールの資本効率を改善することができます。
　上記の式は、式21の分子に類似していることに注意してください。アペンディクスFに示すように、アクセスできないfyDAIの量は、常にシェアの総供給量以上になります。その結果、流動性トークンの総供給量をバーチャルfyDAIリザーブとして使用できます。取引が発生するたびに、バーチャルfyDAIの準備金が実際のfyDAI準備金に追加され、取引の結果を計算するために使用される準備金が決定されます。ただし、(fyDAIの)流動性トークンがミントされるときはいつでも、ミント者はプールのリザーブの実際のfyDAIに比例するfyDAIを提供するだけで済みます。バーチャルfyDAIの準備金は、比例して自動的に増加します（新しく作成された流動性トークンのおかげで、総供給量が比例して増加するため）。

たとえば、アリスが100DAIでプールを初期化するとします。流動性トークンの新しい合計供給量sは100であり、アリスは100の流動性トークンを受け取ります。次に、アリスが時間t=0.5で100fyDAIをプールに販売するとします。これは売りであるため、プールは不変量xend ^1- t/g + yend ^1- t/g =xstart ^1- t/g + ystart ^1- t/g を使用します。 xstartの場合はプールは実際のDAIリザーブ100を使用します。ystartの場合はプールは実際の0のfyDAIリザーブをVirtual fyDAIリザーブに追加します。これで合計供給量sは100に等しくなります。最後に、yendの場合、プールは100のfyDAIをystart（バーチャルリザーブを含む）に追加して200を取得します。xend（g = 0.95）を解くと、結果x = 34.31が得られます。つまり、100 − 34.31 =65.69DAIがコントラクトから送信されます。
ここで、ボブが流動性を追加することにより、10個の新しい流動性トークン（総供給量の10％）を作成するとします。プールには現在34.31DAIがリザーブに入れられているため、ボブは3.43DAIをデポジットします。プールには実際のfyDAIが100しかないため、Bobは10fyDAIをデポジットするだけで済みます。最後に、10個の流動性トークンがボブに割り当てられると、総供給量（バーチャルfyDAIリザーブ）は110に増加します。

次の取引では、ystartの値は100(virtual yfDAI) + 110 (リアルにあるyfDAI) = 210になります。この最適化により、コントラクト初期化時にアクセスできないfyDAIはゼロになります。ただし、取引が行われるとすぐに、手数料によって流動性シェアの価値が高まります。プールが取引手数料を蓄積し、そのfyDAIの値が利息のために増加すると、上記の不変量が増加します。つまり、fyDAIのシェアが増加した分はアクセスできなくなります。

7 Acknowledgments

この論文は、Hayden Adams、Guillermo Angeris、Dmitriy Berenzon、Tarun Chitra、Zubin Koticha、Hart Lambur、Teo Leibowitz、Mikhail Vladimirov、Cyrus Younessi、およびNoahZinsmeisterとの議論に深く感謝しています。著者は、この研究を支援してく
れたParadigmに特に感謝しています。

A Deriving the constant sum formula

以下の微分方程式の解は、xに関して両側を積分し、単純化することにより、constant sum formulaの公式であることを示すことができます。

B Deriving the constant product formula

以下の微分方程式の解は、定数積の公式であることを示すことができます。

まず、方程式を書き直します。

次に、xに関して両側を統合します。

eを各辺の累乗で累乗し、定数e^c1-c2をkとして定義することにより、これを定数積の式として書き直すことができます。

C Deriving the constant power sum formula

以下の微分方程式の解は、「constant power sum formula」の公式であることを示すことができます。

まず、方程式を書き直します。

次に、xに関して両側を積分します。

両側に1-tを掛け、定数 (1-t)・(c1-c2)をkとして定義することにより、これを「constant power sum formula」の式として書き直すことができます。

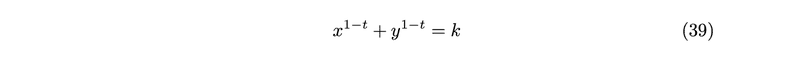
D Deriving the limit of the constant power sum formula as t approaches

tが1に近づくと、「constant power sum formula」の式（x^1-t + y^1-t = xstart^1-t + ystart^1-t ）が一定の積の式（x・y = xstart・ystart）に近づくことを示すことができます。。「constant power sum formula」の式は、yをxの関数にするように書き直すことができます（xstartとystartを定数として使用）。

この関数は、ログ形式で書き換えることができます。

t = 1の場合、方程式の右辺は不定形0/0ですが、L’Hˆopitalの法則を適用すると限界があります。

eを両側の累乗に付加すると、一定の積関数x・y = xstart・ystartが得られます。

E Proving the invariant for total supply

以下の不変条件は、プールが初期化されたときに1から始まり、コントラクトの状態の変化（ミント/バーン、取引、時間の経過）のいずれでも減少しないことを示します。

1-tの不変条件ではなく、この不変条件を使用する理由は、誰かがコントラクトにDAIを直接追加して、fyDAIの価格が1DAIを超える（そしてインプライドレートがマイナスになるような）極端なケースを防止するためです。この状態ではfyDAIの買いは禁止されますが、売りは禁止されません（インプライドレートがプラスに戻るために必要であるため）。金利がマイナスの場合、手数料はプールではなくトレーダーに利益をもたらします。つまり、誰かがfyDAIを1を超える価格でプールに販売すると、1 - t を使用する不変量が減少する可能性があります。上記の不変条件を使用すると、これを回避できます（販売中に直接適用される）。

E.1 Initialization

プールが初期化されると、xstart、ystart、およびsはすべて等しくなります。上記の式で他の変数（xstart、ystart）をsに置き換えると、不変条件の初期値は1であることがわかります。

E.2 Minting and burning

シェアのミントやバーン（x、y、およびsに同じ比率mを掛ける）は、不変量を変更しないことを示すことができます。

E.3 Trading

次に、取引の結果として不変量が減少しないことを示します。 sと 1 - t/gは取引中に変化しないため、分析を簡略化し、この不変量のコア式のみを見ることができます。

これは、セクション5で説明したfyDAIの販売式によって適用される不変量とまったく同じであることに注意してください。その結果、この不変量がfyDAIの購入中にのみ増加することを示す必要があります。上記の不変量は、導関数dy/dxが次のようになるように作成されました。

fyDAIの購入では、「constant power some formula」の公式の異なる調整バージョンを使用します。

この不変量は、導関数dy/dxが次のようになるように構築されたことを思い出してください。

購入には、xの増加とyの減少が含まれます。 xの特定の増加に対して、購入に不変量を使用したyの減少が、もう一方の不変量を使用したyの減少以下であることを示す必要があります。

両側を 1/tの累乗にし、両側の対数を取り、両側にgを掛けると、次のようになります。

g≤1なので、この不等式は、不等式を反転せずに両側をln y /xで除算できる場合に当てはまります。これは、ln y/x>0つまりy>xの場合にのみ当てはまります。 y≤xの場合は常に購入が許可されないため、これはすべての購入に当てはまることが保証され、購入中に不変量が減少することはありません。

E.4 Time

最後に、時間が経過するにつれて（満期までに減少する時間t）、不変量の分子は常に増加する（または同じままである）ことを示すことができます。（不変量の分母は時間の経過とともに変化しないため、無視できます。この係数はtに関する導関数が正になるかどうかは変わらないため、gtではなくtを使用することもできます。）これを行うには、時間に関する偏微分を取り、それが常に0以下であることを示します。