Lec9: 重回帰分析①誤差項の仮定と内生性

皆さんこんにちは。矢野大樹です。前回までで、回帰分析の基礎は一通り完了いたしました。もしまだ消化不良の部分がありましたら、私のnoteなりWooldridgeやStock＆Watsonのテキストを読んで復習しておいてくださいね。

さて、一番最初の記事で、回帰分析は被説明変数と説明変数間の因果関係をはっきりさせるため、極めて厳密な仮定の下実行されると言いました。その極めて厳密な仮定こそが、Lec7で扱った誤差項の仮定と呼ばれるものでした。その中でも特に4番目の仮定は極めて重要でしたね。ただし、この4番目の仮定はなかなか満たされるものではありません。少なくとも単回帰分析では、殆どの場合満たされることがないと言っても過言ではないでしょう。今回は、誤差項の仮定をサラッと復習したうえで、4番目の仮定について、どういう状況の時に破られるかを見ていきます。その上で、4番目の仮定を満たすようなやり方の一つとして、説明変数を増やすという手法を考えたいと思います。

1. 誤差項の仮定

誤差項の仮定は以上の通りです。Ⅰの線形モデルで記述できると言うのは、和の形(足し算の形)で表すことが出来るというものでした。Ⅱの説明変数にバラツキが存在すると言うのは、説明変数が様々な値を取るというものでした。(例えば、説明変数が身長ならば、170cmの人もいれば165cm、180cm、178cmの人もいるなど様々な身長の人がサンプルに含まれている)。Ⅲについては、標本は無作為に抽出されるという意味です。Ⅴは誤差項同士に相関関係が無い、ということを保証するものです。時系列回帰分析の際は破られるケースも多いため、注意が必要です。Ⅵの分散均一については、誤差項のバラツキはどこでも一定というものですが、基本破られます。なので、頑健性のある標準誤差(robust standard error) を最初から使うのがオススメです。Stataだと、コードの末尾に, vce(robust)と打ち込むだけでいいので便利です。Ⅶの仮定はあまり気にしなくて構いません。サンプル数が少ない時に気にするものですが、そもそもサンプル数が少ないと自由度が低くなってしまい、正確な評価が出来なくなりますので、サンプル数は多いほうが良いです。

2: 誤差項の仮定Ⅳ

問題はこの誤差項の仮定Ⅳ：誤差項の条件付期待値は0である　というものでしたね。これは、xを固定したときの誤差項の期待値は0になり、回帰直線yi=β0＋β1xi上の点に一致するというものでした。(下の図参照)

ただし、多くの場合でこの仮定はそう簡単に満たされません。この仮定が満たされない主要因として以下の5つが考えられます。(こうした主要因のことを総称して内生性(endogeneity)と言います。)

1番目の除外された変数が存在する場合とは、原因の一部でもあるにもかかわらず、説明変数に含めていなかった場合に生じるものです。

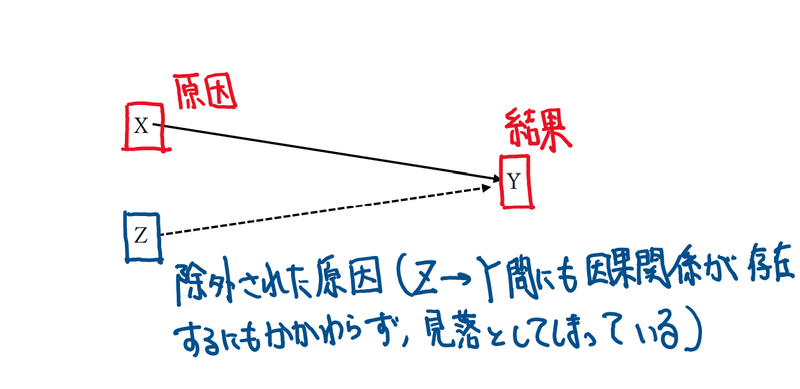
例えば、X,Zが原因で、Yが結果だったとして、説明変数にXだけ(あるいはZだけ)を入れた場合、Z(あるいはX)は原因であるにもかかわらず見落とされてしまいます。(言い方を変えれば、誤差項に説明変数に含まなかったほうの変数が含まれてしまい、被説明変数Yiと誤差項uiが相関してしまいます。)

この場合、係数が過大評価されてしまい(このバイアスのことを省略変数バイアス(omitted variable bias)と言います)、正確な把握が出来なくなってしまいます。こうした事態を避けるのに使われるのが、後述する重回帰分析と呼ばれるものです。

2番目の関数形の特定ミスとは、これは少し難しい内容になります。重回帰分析を進めていく中で少しづつ説明していきますが、説明変数に適切な処理をしなかった場合に生じるものだと思ってください。

3番目の変数の計測誤差とは、データを収集する際にミスが生じることです。例えば、アンケート調査などの入力の際に入力ミスをしてしまうなどです。これはどうしようもありませんが、使うデータがどのような手法で計測されたものであるかや、どのような数式を用いて得られたものであるかは必ず確認するようにしましょう。(卒業論文執筆の際にも、データの出所は勿論のこと、そのデータはどのような手法で収集されたものであるかまで言及する必要があります。)

4番目のセレクションバイアスとは、研究の対象を選択する際に生じるバイアスのことです。例えば、病院に行けば人々は不健康になるのかということを考えれば、あり得ないことだと分かると思います。しかし、健康の度合いと病院に行く回数などを回帰分析すると、統計的に有意な結果が出てしまうのです。これは、病院に行く人そのものがどこか健康上の問題点を抱えているから病院に行くわけであり、病院に行けば不健康になるわけではないのです。なので、病院に行く人を対象にしてしまうとバイアスが発生してしまう、ということになります。セレクションバイアスを取り除くには少し難しい手法を使用する必要があります。機械があれば、紹介したいと思います。

5番目の逆の因果関係や双方向の因果とは、原因と結果の関係が逆であったり、双方向であったりする場合のことです。例えば、広告の数を増やせば収益は上がるか、という問いを考えてみましょう。一見すると、因果関係があるようにも見えますが、そもそも広告を出すには多額の資金が必要です。なので、収益があるからたくさん広告を出しているとも捉えられます。こもように、想定している因果関係とは逆であったり、双方向の因果関係であったりすることはよくあるので、モデルを考察する際には注意する必要があります。(必ず逆の因果関係は無いか検討しましょう)

こうした内生性の問題を克服し、より厳密に因果関係を推定するための手法が計量経済学ではたくさん用意されています。その中の最も基本的な手法が重回帰分析と呼ばれるもので、除外された変数が存在する場合の基本的な対処方針になります。今日からは、この重回帰モデルのついて詳しく見ていきます。

3. 重回帰モデル

単回帰分析に対し、重回帰分析の特徴は説明変数が複数含まれているという点が挙げられます。

単回帰分析の時と同様に、Yiを被説明変数、Xkiを説明変数、βl(l=1...k)を係数、uiを誤差項と言います。今までは説明変数が1個だったのに対し、今回からは説明変数が2個以上になったと考えてください。基本的な考え方は単回帰分析と一緒ですが、説明変数を追加することによって少し複雑になった部分もありますので、次回以降順を追って説明していきます。とりあえず、次回は最小二乗法(OLS)と誤差項の仮定を説明します。次回もどうかよろしくお願いいたします。