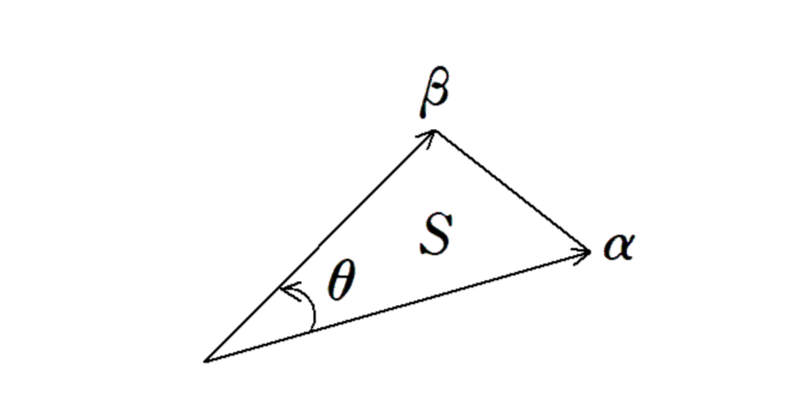
線分OPの通過する面積　～ガウス・グリーンの定理の特殊形～

１．2 つの複素数のなす三角形の符号付き面積

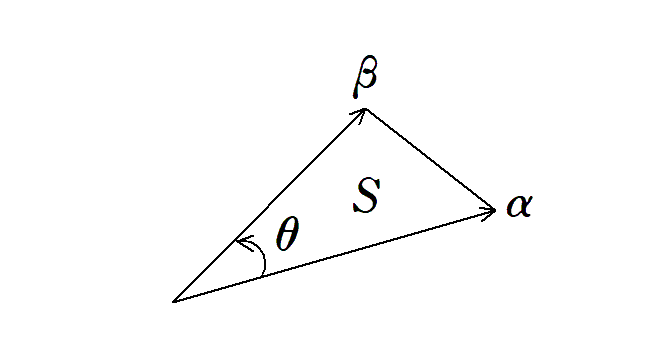
　上の複素数 $${\alpha}$$ ，$${\beta}$$ が張る三角形の符号付き面積を $${S}$$ とすると

$$
①　S=\dfrac{1}{2}\ \mathrm{Im} (\overline{\alpha}\beta)
$$

と表せます。ただし、符号付き面積とは、$${\alpha}$$ から $${\beta}$$ へ反時計回りを正として測った角を $${\theta}$$ とするとき、$${\dfrac{1}{2}\ |\alpha||\beta|\sin{\theta}}$$ で定義します。

【証明】
$${\alpha =r_1e^{\theta_1}}$$,  $${\beta =r_2e^{\theta_2}}$$ とすると
　　$${\overline{\alpha}\beta=r_1e^{-\theta_1}\cdot r_2e^{\theta_2}=r_1 r_2e^{\theta_2-\theta_1}=r_1 r_2e^{\theta}}$$
から
　　$${\dfrac{1}{2}\ \mathrm{Im} (\overline{\alpha}\beta)=\dfrac{1}{2}\ r_1 r_2 \sin{\theta}}$$　【終】

　なお、$${\alpha=a+bi}$$,  $${\beta=c+di}$$ とすると、
　　$${\mathrm{Im}(\overline{\alpha}\beta)=ad-bc}$$
より、有名な結果
　　$${S=\mathrm{Im}(\overline{\alpha}\beta)=\dfrac{1}{2}(ad-bc)}$$
を得ます。

２．OP の通過部分の面積

　次に、点 P の位置が時刻 $${t}$$ の関数であるとき、線分 OP の通過部分の面積の公式を導きます。

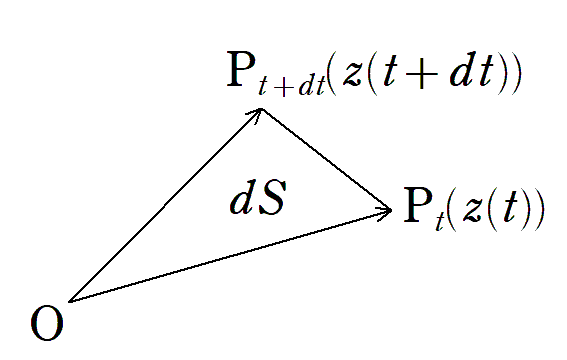
　時刻 $${t}$$ における点 $${\mathrm{P}_t}$$ を表す複素数を $${z(t)}$$ とし、時刻が $${t}$$ から $${t+dt}$$ に増加したときの線分 $${\mathrm{OP}_t}$$ の通過する符号付き面積を $${dS}$$ とすると

$$
②　dS=\dfrac{1}{2}\ \mathrm{Im} \left\{\overline{z(t)}z'(t)\right\} dt
$$

と表せます。

【証明】※ややざっくりです。
時刻が $${t}$$ から $${t+\Delta t}$$ に増加するとき、点 $${\mathrm{P}_t}$$ の位置を表す複素数が $${z(t)}$$ から $${z(t)+\Delta z}$$ に変化したとする。このとき、線分 $${\mathrm{OP}_t}$$ の通過する符号付き面積を $${\Delta S}$$ とすると、①より
　　$${\Delta S}$$
　＝$${\dfrac{1}{2}\ \mathrm{Im} \left[\overline{z(t)}\{z(t)+\Delta z\}\right]}$$

　＝$${\dfrac{1}{2}\ \mathrm{Im} (\overline{z(t)}\Delta z)}$$　　$${(\overline{z(t)}z(t) \in \Reals  より)}$$
から
　　$${\dfrac{\Delta S}{\Delta t}=\dfrac{1}{2}\ \mathrm{Im} \left(\overline{z(t)}\dfrac{\Delta z}{\Delta t} \right)}$$
より　$${\Delta t \rightarrow 0}$$　とすると
　　$${\dfrac{dS}{dt}=\dfrac{1}{2}\ \mathrm{Im} \left\{\overline{z(t)}z'(t) \right\}}$$　【終】

３．例１　双曲線の作る面積

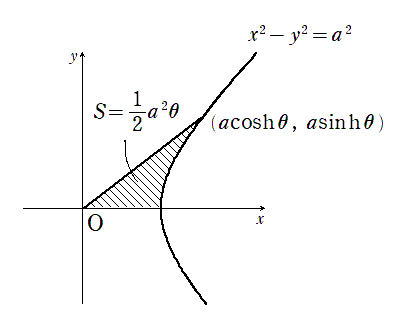
　有名な上の結果を

$$
②　dS=\dfrac{1}{2}\ \mathrm{Im} \left\{\overline{z(t)}z'(t)\right\} dt
$$

を使って導いてみましょう。なお、双曲線関数の初歩についてはこちらをご覧ください。

$${z(t)=a(\cosh{t}+i\sinh{t})}$$　とすると　$${z'(t)=a(\sinh{t}+i\cosh{t})}$$　より
　　$${\mathrm{Im} \left\{\overline{z(t)}z'(t) \right\}}$$
　＝$${a^2(\cosh^2{t}-\cosh^2{t})}$$
　＝$${a^2}$$
から ② より
　　$${dS=\dfrac{a^2}{2}dt}$$
ゆえ
　　$${\displaystyle S=\int_0^{\theta}\dfrac{a^2}{2}dt=\dfrac{1}{2}a^2 \theta}$$
を得ます。

４．例２　ハイポサイクロイドの囲む面積

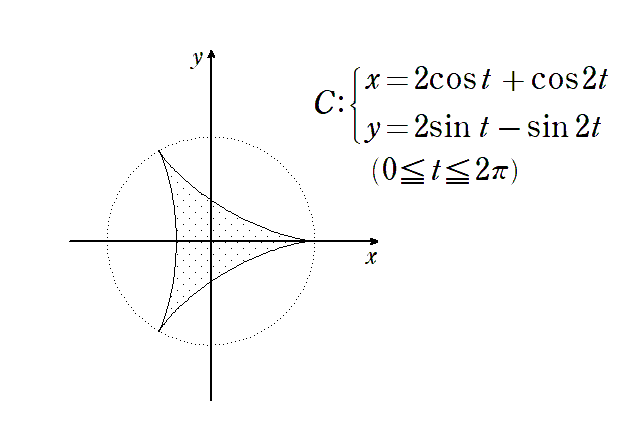
　上のハイポサイクロイドの囲む面積を

$$
②　dS=\dfrac{1}{2}\ \mathrm{Im} \left\{\overline{z(t)}z'(t)\right\} dt
$$

を使って求めましょう。

$${z(t)=2e^{it}+e^{i(-2t)} }$$　とすると
　　$${\overline{z(t)}=2e^{i(-t)}+e^{i(2t)} }$$,
　　$${z'(t)=2ie^{it}-2ie^{i(-2t)}=2i\{e^{it}-e^{i(-2t)} \} }$$
より
　　$${\overline{z(t)}z'(t)}$$
　＝$${2i \{ 2e^{i(-t)}+e^{i(2t)} \} \{ e^{it}-e^{i(-2t)}\} }$$
　＝$${2i \{ 1-2e^{i(-3t)}+e^{i(3t)} \} }$$
から
　　$${\mathrm{Im}\left\{\overline{z(t)}z'(t) \right\} =2(1-\cos{t}) }$$
ゆえ
　　$${dS=(1-\cos{t})dt }$$,
　　$${\displaystyle S=\int_0^{2\pi}(1-\cos{t})dt=2\pi}$$
を得ます。

※グラフを考えると $${\displaystyle \int_0^{2\pi}\cos{t}dt=0}$$