統計学を２級レベルから準１レベルで捉える（準１級対策）

統計とは何か？

全ての事象は『ランダム』で起きる。サイコロで出る目の数字はいくつなのか？コインを投げた時に出るのは表なのか？現実世界で有意義な例をとれば、商品Aに関する広告を閲覧したユーザーが商品Aを購入するのか？
しかし、この『ランダム』さには法則(law of randomness)があり、この法則をできる限り見つけ出す行為が統計と言える。
これをより数学的に理解すれば、ランダムな事象の背景には変数があり、この変数の正体を紐解いていくことが統計である。
この変数を『確率変数』と日本語では呼ぶが、英語のRandom Variableのがこの背景を踏まえるとしっくりくる。

確率変数のデータ型

機械学習でテーブル形式のデータを扱うとき、説明変数や目的変数についてそれぞれデータ型によってはデータの加工を必要としたり、適用するモデルをそもそも変える必要がある。例えば、線形回帰モデルやkNN、SVMなどは全てを数値として扱う必要があるため前処理が必要となる。
統計でも同様であり、統計では数学的な処理や法則を適用するために数値型でない変数は数値に直す必要がある。特に機械学習的に言えばBoolean型の変数を確率に変換してモデルに学習をさせる、統計の世界でもベルヌーイ試行の繰り返しによってできる確率変数を２項分布に従うものとし正規分布で近似するというのは高頻出な問題である。

例題１：
る調査会社が、次の選挙で投票をするかどうかについて、成人500人を無作為に選びアンケートを実施しました。その結果、300人が「投票する」と回答し、200人が「投票しない」と回答しました。このデータに基づいて、「投票する」と回答した人の割合に対する95%信頼区間を求めなさい。
tag: 信頼区間, 二項分布, 正規分布

行列の導入と２次元の確率変数への拡張
統計２級まででは１次元の確率変数または断片的に２次元の確率変数を扱うのみだった。準１級では２次元、もしくは多次元の確率変数を一般化する数式を使うため、行列の知識が必要になってくる。この次元の拡張が理解できるかが準１級では問われる。その入り口になるのが、分散共分散行列だ。
統計２級では分散・共分散をそれぞれ別のものとして捉えていたが、これらは分散共分散行列(Variance Co-variance Matrix)という１つのものとして統一される。

まず、以下の例を考えてみる。
以下の4つの物件のデータがある。それぞれの物件には、部屋の数とその物件の価格が1000ドル単位で記録されている。これらのデータを使って、部屋の数と価格の関係性を分析するとする。

統計２級であれば、ピアソンの相関係数の公式に値を代入するだろう。
統計準１級の考えであれば各レコードを２次元のベクトルと捉え、平均値から差し引いたものをベクトルの大きさとする。
例えば最初のレコードであれば、(2-3.5, 150-262.5) = (-1.5, -112.5)のベクトルになる。同様に全てを計算する。

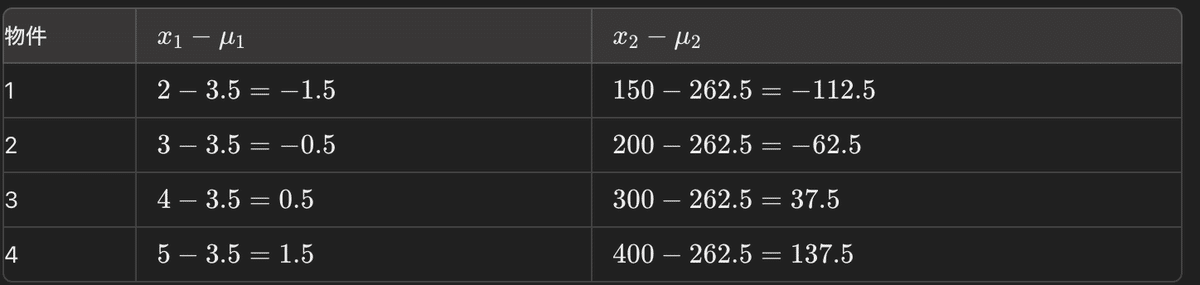
これを行列Xとすると、Xは以下のように描写される。

$$
X = 
\begin{pmatrix}
-1.5 & -112.5 \\
-0.5 & -62.5 \\
0.5 & 37.5 \\
1.5 & 137.5
\end{pmatrix}
$$

分散共分散行列は以下のように計算できる。

$$
S = \frac {1}{N}X^TX              (1)
$$

Xを代入すると結果は以下のようになる。

$$
S = 
\begin{pmatrix}
1.25 & 106.25 \\
106.25 & 9218.75 \\
\end{pmatrix}
$$

この対角にない要素の106.25こそが、部屋の数と価格の共分散を表す。
これは１次元の分散を考える時と実は全く同じことをしている。
要は、部屋の分散に絞ったとき、

$$
X = 
\begin{pmatrix}
-1.5 \\
-0.5 \\
0.5 \\
1.5 
\end{pmatrix}
$$

として、(1)に代入してやれば分散が求まるのである。

このように統計２級でスカラー的な扱いをしていたものを行列またはベクトルで考えるようになることが統計準１級の真髄であり、だからこそ統計学実践ワークブックはいろいろ寄り道をしつつ２６章の多変量解析、つまり多次元データの解析へ向かっていくのだと筆者は考える。

また、ここで求まった分散共分散行列は正方行列であるので、行列の様々な公式を使うことができる。統計準１級では、または機械学習においても、分散共分散行列は様々なところで多用される。
統計２級合格の時点でこの分散共分散行列に馴染みがない。そんな人には分散共分散行列＝多次元での分散と考えておけばいい。

主成分分析
主成分分析(Principle Component Analysis)はこの初歩の応用ともいえ、機械学習でも馴染みのある分野だと思う。
主成分分析では「分散」＝「情報」と捉える。つまり、分散が大きいほど捉える情報が大きい、ということになる。
ここで多次元の分散は分散共分散行列で表され、分散共分散行列は対象でかつそれぞれの値が実数のため必ず固有ベクトルと固有値を持ち合わせる。
固有ベクトルは互いに直行し合う特性を生かし、新たな次元として活用できる。固有値(λ)は行列の大きさ、つまりここでは分散＝情報の大きさを示すため固有値(λ)が大きければ大きいほどそれが主成分となる。つまり固有値が最大の固有ベクトルが第一主成分と言える。

ピアソン、フィッシャー
統計を知るということはその歴史を知ることでもある。統計の手法や法則にはそれを発見した人の名前がよく使われ、その名前は知っておく必要がある。中でもフィッシャー(Ronald Fisher)とピアソン(Karl Pearson)が残した功績は押さえておく必要がある。例えば、F検定のFはFisherが発明したことから由来される。フィッシャーの３原則(Fisher's Three Principles)やピアソンの相関係数(Karl Pearson's Coefficient of Correlation)とうも必ず覚えておく必要がある。

偏微分とラグランジュの未定乗数法
統計準１級では微積分が多用される。偏微分が使われる１例としてラグランジュの未定乗数法(Lagrange Multiplier)がある。このラグランジュの未定乗数法は極値を求める上で非常に便利なので統計でよく使われる。
例えば、主成分分析で分散を最大にさせるような固有ベクトルを求めたり、フィッシャーの判別分析(Linear Discriminant Analysis)ではクラス別の平均ベクトルの差であるm2-m1を直行し、クラス内分散を最小にかつクラス間分散を最大とするような最適なベクトルwを求める際にも使われる。

作成中。