同軸ケーブルの電磁気学的考察

これは大学無線部 Advent Calendar 2023 17日目の記事です。

adventar.org

自己紹介

こんにちは、JA1ZLOに所属しているOTAです。コールサインはないので、実質NO NAMEですね。学科としては応用物理系に所属しています。
最近、私は光通信を学んだのですが、光ファイバではエネルギー減衰が起こっており、

写真のように、可視光領域で損失が下がっています。これらは光ファイバの材料である「誘電体」によって起こされる損失です。という事は、誘電体が入っている同軸ケーブルも同様な損失があるのではないでしょうか？
という事で、同軸ケーブルの損失の周波数特性を目標に、同軸ケーブルについて電磁気学的に考え直すことにします。

同軸ケーブルの太さ

太さの種類は、1.5D,3D,5D,8D,10D,12Dがありますね(富士無線より)。12Dは見たことがない気がしますが、太いメリットは何なのでしょうか？
以前は、太いと抵抗が下がる(並列の合成抵抗の気持ち)ことがメリット、と聞き納得しましたが、もともと同軸ケーブルの内部抵抗は大きくないですし、同軸ケーブルの特性インピーダンス50Ωというのは、並列になるとどうこうという物ではないでしょう。

実際、

JARLのどっかのページより

となり、太さを変えても、最大3dB/10m($${\frac{1}{\sqrt{2}}}$$倍)程度です。ここでは、太くする理由を電磁波のモードの観点から触れてみましょう。

まずマクスウェル方程式

$$
\left\{
  \begin{array}{lcccl}
    div E &:=& \nabla \cdot E &=& \frac{\rho}{\epsilon}　(ガウスの法則)\\
    div B &:=& \nabla \cdot B &=& 0　(磁場の湧き出しなし)\\
    rot E &:=& \nabla \times E &=& -\frac{\partial B}{\partial t}　(電磁誘導)\\
    rot B &:=& \nabla \times B &=& \mu J + \epsilon \mu\frac{\partial E}{\partial t}\\
  \end{array}
\right.
$$

を用いて、電荷がなく($${\rho = 0}$$)電流もない($${j=0}$$)のいつもの空間を考えると、

$$
\begin{equation*}
  \begin{split}
    rot(rot E) &= e_{i}\epsilon_{ijk} \partial_{j} (rot E)_{k}\\
    &= e_{i}\epsilon_{ijk} \partial_{j} \epsilon_{klm} \partial_{l}E_{m}\\
    &= e_{i}\epsilon_{kij}\epsilon_{klm}\partial_{j}\partial_{l}E_{m}\\
    &= e_{i}\left(\delta_{il}\delta_{jm} - \delta_{im}\delta_{jl}\right)\partial_{j}\partial_{l}E_{m}\\
    &= e_{i}\left(\partial_{i}\partial_{j}E_{j} - \partial_{j}\partial_{j}E_{i}\right)\\
    &= \nabla\left(\nabla \cdot E\right) - \nabla^2E\\
    また、&\\
    rot(rot E) &= -\frac{\partial}{\partial t}\nabla \times B\\
    &= -\epsilon \mu\frac{\partial^2E}{\partial t^2}\\
  \end{split}
\end{equation*}
$$

であることより、

$$
\nabla^2 E= \epsilon \mu\frac{\partial^2E}{\partial t^2}
$$

同様に、

$$
\nabla^2 B= \epsilon \mu\frac{\partial^2B}{\partial t^2}
$$

という波動方程式を得ます。
ここで、進行方向(z軸の方向とする)に対して、減衰係数を$${\gamma}$$と置きます($${e^{-\gamma z} }$$で減衰)。
そのような波については、波動方程式は次のように変形されます。但し、$${E,B}$$は$${E=E_0 e^{-\gamma z}e^{i\omega t}}$$,$${B=B_0 e^{-\gamma z}e^{i\omega t}}$$のような形で書けると考えた。

$$
\begin{equation*}
  \begin{split}
    \left\{
      \begin{array}{ccc}
        \frac{\partial^2 E_z}{\partial x^2} + \frac{\partial^2 E_z}{\partial y^2} + \gamma^2 E_z &=& -\omega^2\epsilon \mu E_z\\
        \frac{\partial^2 B_z}{\partial x^2} + \frac{\partial^2 B_z}{\partial y^2} + \gamma^2 B_z &=& -\omega^2 \epsilon \mu B_z
      \end{array}
    \right.
    &\Leftrightarrow
    \left\{
      \begin{array}{ccc}
        \frac{\partial^2 E_z}{\partial x^2} + \frac{\partial^2 E_z}{\partial y^2} &=& -k_c^2 E_z\\
        \frac{\partial^2 B_z}{\partial x^2} + \frac{\partial^2 B_z}{\partial y^2} &=& -k_c^2 B_z\\
      \end{array}
    \right.\\
    & (k_c^2 = \gamma^2 + \epsilon \mu \omega^2と置いた)\\
  \end{split}
\end{equation*}
$$

と、ヘルムホルツ方程式を得る。これに適切な境界条件(電波を伝える管の形状などによって変わる)を与えると、解ける。
また、$${E_x,E_y,B_x,B_y}$$についても、マクスウェル方程式より

$$
\begin{equation*}
  \begin{split}
    \left\{
      \begin{array}{ccc}
        \frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} &=& -j\omega B_x\\
        \frac{\partial E_x}{\partial z} - \frac{\partial E_z}{\partial x} &=& -j\omega B_y\\
        \frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y} &=& -j\omega B_z\\
        \frac{\partial B_z}{\partial y} - \frac{\partial B_y}{\partial z} &=& j\omega \epsilon \mu E_x\\
        \frac{\partial B_x}{\partial z} - \frac{\partial B_z}{\partial x} &=& j\omega \epsilon \mu E_y\\
        \frac{\partial B_y}{\partial x} - \frac{\partial B_x}{\partial y} &=& j\omega \epsilon \mu E_z\\
      \end{array}
    \right.
    &\Leftrightarrow
    \left\{
    \begin{array}{ccc}
      \frac{\partial E_z}{\partial y} + \gamma E_y &=& -j\omega B_x\\
      -\gamma E_x - \frac{\partial E_z}{\partial x} &=& -j\omega B_y\\
      \frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y} &=& -j\omega B_z\\
      \frac{\partial B_z}{\partial y} + \gamma B_y &=& j\omega \epsilon \mu E_x\\
      -\gamma B_x - \frac{\partial B_z}{\partial x} &=& j\omega \epsilon \mu E_y\\
      \frac{\partial B_y}{\partial x} - \frac{\partial B_x}{\partial y} &=& j\omega \epsilon \mu E_z\\
    \end{array}
    \right.\\
    &\Rightarrow
    \left\{
      \begin{array}{ccc}
        k_c^2 E_x &=& -j\omega \frac{\partial B_z}{\partial y}-\gamma \frac{\partial E_z}{\partial x}\\
        k_c^2 E_y &=& j\omega \frac{\partial B_z}{\partial x}-\gamma \frac{\partial E_z}{\partial y}\\
        k_c^2 B_x &=& j\omega \mu \frac{\partial E_z}{\partial y}-\gamma \frac{\partial B_z}{\partial x}\\
        k_c^2 B_y &=& -j\omega \mu \frac{\partial E_z}{\partial x}-\gamma \frac{\partial B_z}{\partial y}\\
      \end{array}
    \right.\\
  \end{split}
\end{equation*}
$$

となる。

TEM波

まず、進行方向(z)に電場、磁場の成分を持たない($${E_z=0,B_z=0}$$)場合を考える。TEM波と呼ばれる。
すると、$${k_c^2 = \gamma^2 +\omega^2 \epsilon \mu =0}$$がこのような波の存在する条件となる。即ち、$${\gamma(減衰係数)=\pm j\omega \sqrt{\epsilon \mu}}$$であり(純虚数)、z方向に進行する減衰しない波となった。
位相速度は、この波がz方向への進行波であること($${jk\cdot r=j|k|z=\gamma z}$$)に注意して、$${\frac{\omega}{|k|}=\frac{1}{\sqrt{\epsilon \mu}}\left(=\frac{c^2}{\sqrt{\epsilon_r \mu_r}}\right)}$$となる。($${\epsilon_r,\mu_r}$$はそれぞれ、比誘電率、比透磁率である為、光速よりも少し遅くなることも分かる。)
また、この時、静電ポテンシャル$${\phi}$$を導入すると、$${\nabla \phi=E}$$である。今、$${div{E}=0}$$より、$${E_z=0}$$であることに注意すると、

$$
\nabla \cdot{E} = \frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}=0
$$

のラプラス方程式を得る。
これを解けば、$${E}$$が分かり、$${B}$$も分かる為、同軸ケーブルの中の電磁波の電波の様子が分かる。
同軸ケーブル内では、回転対称性がある為、極座標で考えるのが見通しが良い。よって、ラプラス方程式を2次元極座標(3次元円筒座標)で考えると、

$$
\frac{\partial^2 \phi}{\partial r^2} + \frac{1}{r}\frac{\partial \phi}{\partial r} +\frac{1}{r^2}\frac{\partial^2 \phi}{\partial \theta^2} = 0
$$

という式になる。$${\phi = R(r)\Theta(\theta)}$$という変数分離形の解となると考えて解くと、

$$
\begin{equation*}
  \begin{split}
    \left(\frac{d^2 R}{dr^2} + \frac{1}{r}\frac{dR}{dr}\right)\Theta(\theta) = -\frac{R(r)}{r^2}\frac{d^2\Theta}{d\theta^2}
    &\Leftrightarrow \left(\frac{d^2 R}{dr^2} + \frac{1}{r}\frac{dR}{dr}\right)\frac{r^2}{R(r)} = \frac{d^2\Theta}{d\theta^2}\frac{1}{\Theta(\theta)}\\
    &左辺はrのみの関数で、右辺は\theta のみの関数である為、定数(m^2)であると置けて、\\
  \end{split}
\end{equation*}
$$

$$
\begin{equation*}
  \begin{split}
    \left\{
    \begin{array}{ccc}
      \frac{d^2 R}{dr^2} + \frac{1}{r}\frac{dR}{dr} - m^2 \frac{r^2}{R(r)} &=& 0\\
      \frac{d^2\Theta}{d\theta^2} - m^2 \Theta(\theta) &=& 0\\
    \end{array}
    \right.
    &\Leftrightarrow
    \left\{
    \begin{array}{ccc}
      \frac{d^2 R}{dr^2} + \frac{1}{r}\frac{dR}{dr} - m^2 \frac{r^2}{R(r)} &=& 0　(本当はベッセル関数が解になる)\\
      \Theta(\theta) &=& c_1 \cos(m\theta) + C_2 \sin(m\theta)\\
    \end{array}
    \right.\\
    同軸ケーブルでは&回転対称性より、\Theta は定数となることより、m=0\\
    &\Leftrightarrow
    \left\{
    \begin{array}{ccc}
      \frac{d^2 R}{dr^2} + \frac{1}{r}\frac{dR}{dr} &=& 0\\
      \Theta(\theta) &=& C_1\\
    \end{array}
    \right.\\
    &\Leftrightarrow
    \left\{
    \begin{array}{ccc}
      \frac{dR}{dr} &=& C_3\frac{1}{r}\\
      \Theta(\theta) &=& C_1\\
    \end{array}
    \right.\\
    &\Leftrightarrow
    \left\{
    \begin{array}{ccc}
      R(r) &=& C_3\ln r +C_4\\
      \Theta(\theta) &=& C_1\\
    \end{array}
    \right.\\
  \end{split}
\end{equation*}
$$

となる。半径方向の電場$${E_r}$$は、$${E_r=-\frac{d\phi}{dr}}$$で求まるから、

$$
E_r = -\frac{C_3 C_1}{r} = V_0 \frac{1}{r}　(V_0:=C_3 C_1 とおいた)
$$

となる。芯線と外部導体間の電位は、

$$
\int_{a}^{b}E_r dr = V_0 \ln \frac{b}{a}
$$

である。回転対称性より$${E_\theta = 0}$$
$${E_z =0,B_z=0}$$の下で、マクスウェル方程式を考えると、

$$
\begin{equation*}
  \begin{array}{ccc}
    j\omega \sqrt{\epsilon \mu}E_x = j\omega B_y\\
    j\omega \sqrt{\epsilon \mu}E_y = -j\omega B_x\\
  \end{array}
\end{equation*}
$$

となる為、$${\frac{E_x}{B_y} = -\frac{E_y}{B_x} = \frac{1}{\sqrt{\epsilon \mu}}}$$より

$$
B_\theta = \sqrt{\epsilon \mu}E_r = V_0 \frac{\sqrt{\epsilon \mu}}{r}
$$

で、$${E_\theta = 0}$$である。よって、アンペールの法則より、芯線を通る電流$${I}$$は

$$
I = \frac{1}{\mu}\oint_{r=a} B_\theta ds = \frac{1}{\mu} \int_{0}^{2\pi}V_0 \frac{\sqrt{\epsilon \mu}}{a} ad\theta = 2\pi V_0 \sqrt{\frac{\epsilon}{\mu}}
$$

である。よって、特性インピーダンスは

$$
Z=\frac{V_0\ln \frac{b}{a}}{2\pi V_0 \sqrt{\frac{\epsilon}{\mu}}} = \frac{1}{2\pi}\sqrt{\frac{\mu}{\epsilon}}\ln\frac{b}{a}
$$

であり、芯線の半径を$${d}$$,外部導体までの半径を$${D}$$と置くと、

$$
Z  \fallingdotseq \frac{138}{\sqrt{\epsilon_r}}\log_{10} \frac{D}{d}
$$

という見慣れた形になました。後述する理由で$${\frac{D}{d}=3.59112\dots}$$であるのが最適である。同軸ケーブルの形状を支えるPEの比誘電率は$${2.3～2.4}$$程度であることを考えると、

$$
Z = \frac{138}{\sqrt{2.35}\log_{10}(3.59112)} \fallingdotseq 49.98250
$$

となり、50Ωの特性インピーダンスとなる。
比誘電率が約$${1}$$、即ち空気であるとき、この値は75Ωになる。

D/d=3.59112にする理由

ここで、本題の同軸ケーブルの誘電損失の話に入る。長さ$${l}$$の同軸ケーブルを通して、電力$${P}$$を伝えることを考える。($${P=ZI^2}$$で入力。)表皮効果より、表皮深さ$${\delta}$$よりも深いところでは電流が生じないと考える。また、金属の抵抗率を$${\rho}$$と置く。すると、損失$${P_l}$$は

$$
\begin{equation*}
  \begin{split}
    P_l &= 芯線での消費電力 + 外部導体での消費電力\\
    &= \rho \frac{l}{2\pi d\delta}I^2 + \rho \frac{l}{2\pi D\delta}I^2\\
    &= \frac{\rho l}{2\pi \delta D}\left(\frac{D}{d}+1\right)\frac{P}{\frac{1}{2\pi}\sqrt{\frac{\mu}{\epsilon}}\ln\frac{D}{d}}\\
    &= \frac{\rho l}{\delta D}\sqrt{\frac{\epsilon}{\mu}}\frac{\frac{D}{d}+1}{\ln\frac{D}{d}}P \propto \frac{\frac{D}{d}+1}{\ln\frac{D}{d}}\\
  \end{split}
\end{equation*}
$$

である為、損失が最小になるには、$${\frac{\frac{D}{d}+1}{\ln\frac{D}{d}}}$$が最小となることが必要。よって、物理的制約から$${\frac{D}{d}>1}$$に注意すると、

desmosより

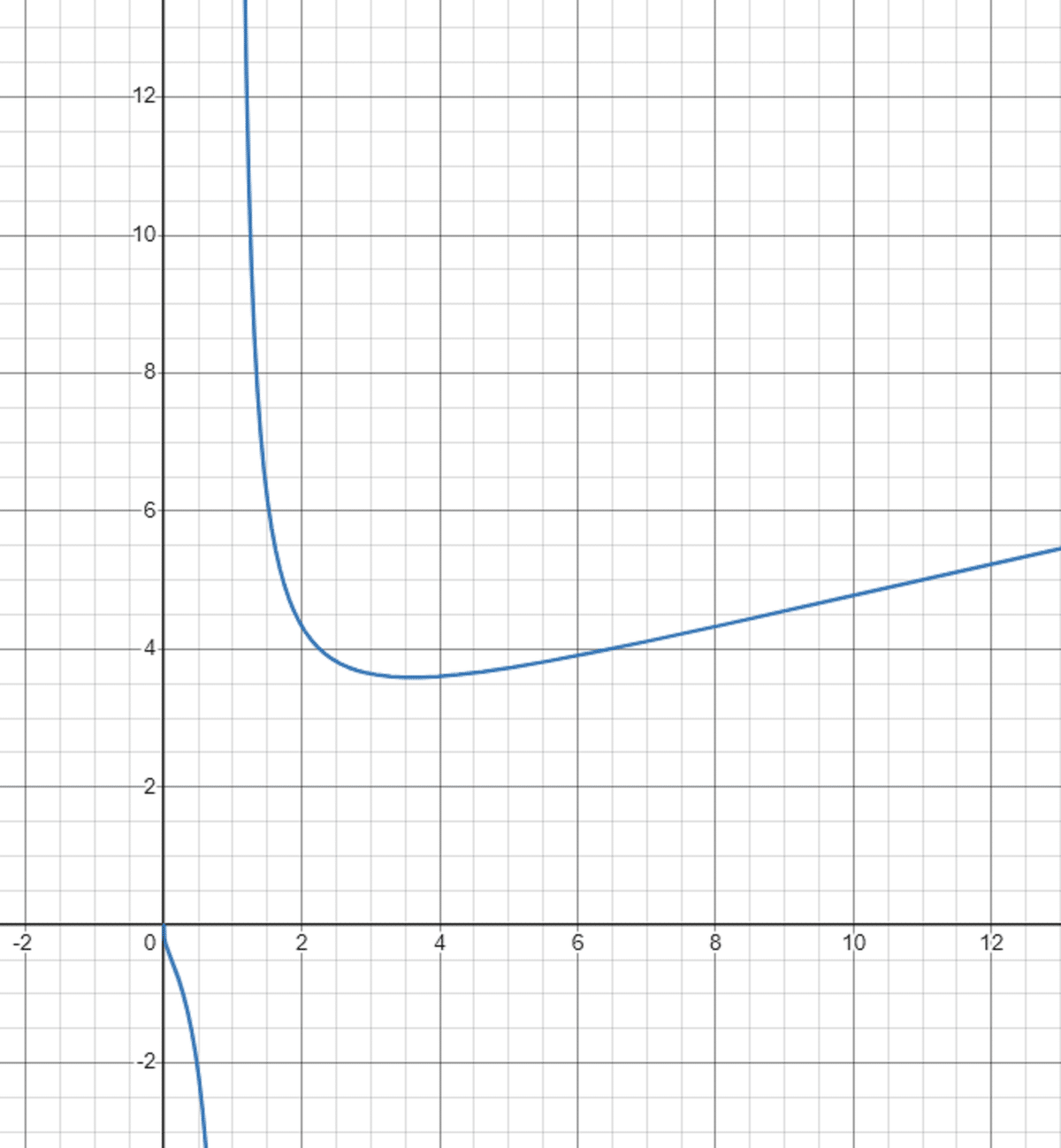
より、$${\frac{D}{d}=3.59112}$$辺りが最適となる。

$$
P_l = \frac{\rho l}{\delta D}\sqrt{\frac{\epsilon}{\mu}}\frac{\frac{D}{d}+1}{\ln\frac{D}{d}}P　(再掲)
$$

次に、表皮深さについて、$${\delta = \sqrt{\frac{\rho}{\pi f\mu}}}$$であることも踏まえると、損失は、$${P_l \propto f^{\frac{1}{2}}}$$であると分かり、高周波ほど損失が大きい。
また、$${D}$$が大きくなると、損失は$${D^{-1}}$$の速度で小さくなるため、$${\frac{D}{d}}$$を一定に保って$${D}$$を大きくする(太くする)とロスも少なくなる。
よって、同軸ケーブルを(可能なら無限に)太くすればよいように思われます。しかし、実は太くし過ぎても良くないようです。

まず、TEM波を使いたい(それ以外の高次のモードは使いたくない)という前提で考えます。

TE波

TE波は電場の進行方向成分がないものである($${E_z=0}$$)。TEM波同様、ヘルムホルツ方程式からスタートして、

$$
\frac{\partial^2 B_z}{\partial x^2} + \frac{\partial^2 B_z}{\partial y^2} + k_c^2 B_z = 0
$$

を変数分離系$${B_z = R(r)\Theta(\theta)}$$の形になると考えて解くと、同様に、定数$${m^2}$$を用いて、

$$
\begin{equation*}
  \begin{array}{rcl}
    \frac{d^2R}{dr^2}+\frac{1}{r}\frac{dR}{dr}+\left(k_c^2 -\frac{m^2}{r^2}\right)R(r) &=& 0\\
    \frac{d^2\Theta}{d^2\theta} + m^2\Theta(\theta) &=& 0\\
  \end{array}
\end{equation*}
$$

より、前者に関しては、ベッセルの微分方程式となっており、

$$
R(r) = C_2 J_m(k_c r) + C_3 N_m(k_c r)
$$

と表せる。$${J_m}$$はベッセル関数、$${N_m}$$はノイマン関数。

後者に関しては、一周すると元に戻る条件も考えると、$${m\in \mathbb{Z}}$$という条件下で、

$$
\Theta(\theta) = C_1\cos\left(m\theta - \theta_0\right)
$$

と表せる。
$${N_m(k_c r)}$$は$${r=0}$$で発散する関数であるが、同軸ケーブルの芯線の半径$${a}$$がある程度大きいと考えると問題ない。$${E_\theta =\frac{j\omega}{k_c^2}\frac{\partial B_z}{\partial r}}$$であるため、

$$
\begin{equation*}
  \begin{split}
    E_\theta = 0 &\Leftrightarrow \frac{\partial B_z}{\partial r}=\frac{dR}{dr}=0\\
    &\leftrightarrow C_2 k_c \frac{dJ_m}{dr} + C_3 k_c \frac{dN_m}{dr} = 0\\
  \end{split}
\end{equation*}
$$

であることより、境界条件境界条件$${E_{\theta}=0　(r=d,D)}$$は、

$$
\begin{equation*}
  \left\{
  \begin{array}{ccc}
    C_2 \frac{dJ_m}{dr}|_{r=d} + C_3 \frac{dN_m}{dr}|_{r=d} &=& 0\\
    C_2 \frac{dJ_m}{dr}|_{r=D} + C_3 \frac{dN_m}{dr}|_{r=D} &=& 0\\  \end{array}
  \right.
  \Leftrightarrow
  \begin{pmatrix}
    \frac{dJ_m}{dr}|_{r=d} & \frac{dN_m}{dr}|_{r=d}\\
    \frac{dJ_m}{dr}|_{r=D} & \frac{dN_m}{dr}|_{r=D}
  \end{pmatrix}
  \begin{pmatrix}
    C_2\\
    C_3
  \end{pmatrix}
  =
  \begin{pmatrix}
    0\\
    0
  \end{pmatrix}
\end{equation*}
$$

ここで、$${(C_2,C_3)\neq (0,0)}$$である解が存在する必要十分条件は

$$
\frac{dJ_m(k_c r)}{dr}|_{r=d} \frac{dN_m(k_c r)}{dr}|_{r=D} - \frac{dJ_m(k_c r)}{dr}|_{r=D} \frac{dN_m(k_c r)}{dr}|_{r=d} = 0
$$

である。これを$${k_c}$$に関する方程式と見たとき、最小の解は近似的に、$${k_c = \frac{2}{d+D}}$$で与えられる。よって、カットオフ周波数の波長は

$$
\lambda_c = \frac{2\pi}{k_c} = \pi(d+D)
$$

である。この波長よりも長い周波数を用いれば、同軸ケーブル内をTEM波のみが伝播し、高次のモードの波は通らなくなる。よって、(d+D)が小さい程TEM波だけ発生させやすくなる。
故に、同軸ケーブルは太すぎても良くない。

あとがき

これまで、先輩に倣いやってきたことを理論的に保障できたのはとても面白かったです。数式を書いていたらめちゃ長になってしまいましたが、ここまで読んでくださった方ありがとうございました。
本当は同軸ケーブルの導体損失($${\sqrt{f}}$$に比例するやつ)だけでなく、誘電体損失($${f}$$に比例するため、高周波で支配的)もやってみたかったのですが、時間がないのと、難しく、良い教材も見つからなかったことから今回は諦めました。

良ければ皆さんもアマチュア無線を物理の世界で楽しまれてください！！

参考文献

•  長谷部望. 電波工学. コロナ社, 1995.

•  中野義昭. 電磁波工学の基礎. 数理工学社, 2015.

•  ファイバーラボ株式会社. "レイリー散乱". https://www.fiberlabs.co.jp/tech-word/rayleigh-scattering/. (参照:2023/12/16)

•  富士無線電機. "50Ω同軸ケーブル価格表". https://www.fujimusen.co.jp/coaxial/index.html. (参照:2023/12/16)

•  日本アマチュア無線連盟. "同軸ケーブルの損失". https://www.jarl.org/Japanese/7_Technical/lib1/coax.htm. (参照:2023/12/16)

•  株式会社Y.E.I.. "比誘電率表". https://www.yei-jp.com/tech-infor/dielectric/dielectric.html. (参照:2023/12/17)