公式を投げ出して確率をブチのめすか~
こんにちは。
学問のターンです。
マジメに計算はしなくていいです。直感でテキトーに考えてみてください。
あなたのお隣に双子さんが引っ越してきたようだ。
ある日あなたは、その家から女の子が出てくるのを見かけた。双子の片割れらしい。
さてこのとき、双子のもう一人も女の子である確率は?
どうなんでしょうか。
男か女なんだから $${\displaystyle \frac{1}{2}}$$ と答えたくなります。
しかしながら正解はなんと $${\displaystyle \frac{1}{3}}$$ なんです。
え?
何その 3 どっから来たん?
てか $${\displaystyle \frac{1}{2}}$$ じゃダメなん? 実は $${\displaystyle \frac{1}{2}}$$ だったりしない?
ちゃんと説明しましょう。この問題は「条件つき確率」というものが絡んできます。
えっと、どんな公式だっけな…
$$
P(B|A)=\frac{P(A \cap B)}{P(A)}
$$
あっ大丈夫っす…
とまあ、得てして確率の問題というのは納得感の薄く、公式も意味をつかみづらいものです。
あやふやなものを扱うため、なぜそうなるのか? というのがなかなか見えないからですね
そこで今回はこんなものを用意しました。

実はこれ、運命を操作できるんです。
この盤面を回転させ、目隠しをして矢を投げます。

見事「表」に当たりました。では、コイントスをしてみましょう。



はい、「表」が出ました。
そうなんです。「表」に当たると、次のコイントスで必ず「表」が出るようになるんです。便利~
ただしチャンスは 1 回だけ。一度出た結果は変えられません。
うまく使えばいくらでも悪用できそうですが、今回のテーマはそこではなく。
要するに、↓これ↓を見れば「表」も「裏」も確率 1/2 だってのがハッキリわかるんですね。
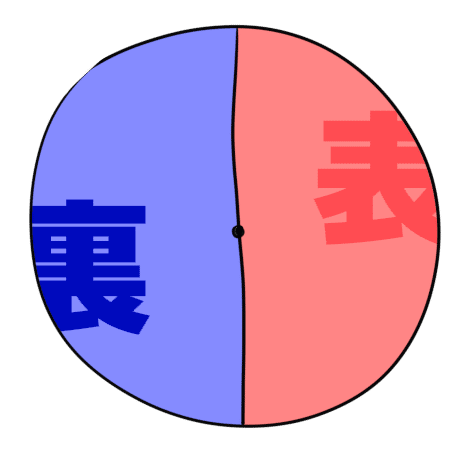
ほかにもサイコロ版もあります。

使い方も効果も一緒です。これだと確率はどれも $${\displaystyle \frac{1}{6}}$$ ですよね。
これだけだとだから? って感じですが、実は新機能がついてるんです。
それがこちら。

なんと一部を欠けさせることができちゃうんです。
この状態で矢を投げてみましょう。

あら、当たらなかったかな
ではもう一度…

音がしたので今度は当たったみたいです。
さて、何に当たったんでしょうか?
盤面には偶数だけを残したので、2 か 4 か 6 の $${\displaystyle \frac{1}{3}}$$ ですよね…
…
と、これが「条件つき確率」なんです。
もともと $${\displaystyle \frac{1}{6}}$$ だったのが、偶数という“条件”がついたことで $${\displaystyle \frac{1}{3}}$$ に変化した。
盤面でいうなら、奇数という“ノーカウント”のエリアがある、ということになります。
“ノーカウント”は数えません。矢が当たらなければやり直しです。
このせいで、わけのわからん数字が出てきたりするんですね。
確率のムズい問題にはだいたいコイツが絡んでるんだ。
一応上の状況を問題のように書いてみます。
6 面サイコロを 1 回投げた。
いま、偶数が出たことがわかっている。
このとき、出た目が 4 である確率はいくつか。
答えは $${\displaystyle \frac{1}{3}}$$ です。2 か 4 か 6 なので。
では、最初の問題に戻りましょう。
盤面も無地のものを用意しました。

さて、双子の性別についての話なので、まずこんな風に分けられますね。

続いて、女の子がいることがわかりました。
ということは、両方男の子(兄弟)である可能性は消えるわけです。

さてこのとき。両方女の子(姉妹)なのは?
もちろん $${\displaystyle \frac{1}{3}}$$ ですよね。
この突飛に見える 3 は、性別の全 4 パターンからあり得ない 1 パターンを引いたものだったんです。
盤面を使うことで、厄介な条件つき確率も少しは扱いやすくなるのではないでしょうか。
そうでもないか。
(参考)
この考え方は以下の書籍「プログラミングのための確率統計」(著 : 平岡和幸・堀玄)に大きくインスパイアを受けています。タイトルにプログラミングとありますが、内容はそれほどプログラミングによっておらず誰でも読めるんじゃないかなと思います。この考え方を広げて期待値や連続値を取る確率、統計なんかにまで話してくれているのでとてもよいです。同シリーズの「プログラミングのための線形代数」もオススメ。
(追記)
もう少し例題でも出そうかと思って調べてたら既にちゃんとした記事があって笑っちゃった
詳しくわかりやすく書いてあるので読もう↓
(おまけ問題)
8 回に 1 回電車を乗り過ごす人がいる。この人は月曜になるとグデングデンになって 2 回に 1 回は乗り過ごしてしまうらしい。この人が電車を乗り過ごしたとき、月曜である確率はいくらか。ただし、土日は電車には乗らない。
まず何曜なのかについてなので、こう描ける。
火曜~金曜を区別する意味はないので、まとめてしまう。

続いて月曜以外に乗り過ごすのが $${\displaystyle \frac{1}{8}}$$ なので、こう。

同じように、月曜に乗り過ごすのが $${\displaystyle \frac{1}{2}}$$ なので、こう。

なので、乗り過ごしたときの盤面はこうなります。

どちらも計算すると $${\displaystyle \frac{1}{10}}$$ になるので、月曜とそれ以外ではトントンということになります。
よって、乗り過ごしたときは $${\displaystyle \frac{1}{2}}$$ で月曜日。
この記事が気に入ったらサポートをしてみませんか?
