「アルマゲドンルール」に関する考察
ある日、こんなツイートが目に留まりました。Jump Kingというゲームのスピードラン世界大会におけるルールが面白い、とのこと。
今週末の世界大会は1回戦が魂の1先で、
— らー油まん (@laayuman) February 15, 2024
2回戦から2先なんだけど、その2先のルールが面白いことになってた pic.twitter.com/l7pePPg8tE
確かに面白い。速いタイムを宣言したほうが一方的勝利を狙えるが、失敗するリスクも上がる、という駆け引きがありそうです。こういうのを見ると「どうするのが最適な戦略なんだろう?」と真面目に考えてしまう性格でして、その結果をまとめてみたのがこの記事です。数学の話がちょっと出てきます。Jump Kingの話は出てきません。そもそも未プレイです。興味はある。
1 問題定義
1.1 問題の置き換え
改めてルールを確認しましょう。
あらかじめ自分が突破できると思うタイムを運営に宣言する(始まるまでお互いに公開されない)
宣言したタイムが速いほうが先に走り、成功(宣言したタイム以内にクリア)したら先手が勝利
先手が失敗した場合、後手が成功したら後手が勝利
二人とも失敗した場合、速くクリアしたほうが勝利
全く同じタイムを宣言してしまった場合については何も書かれていませんが、ここでは考えないこととします(おそらく普通に並走するのでしょうか…)。
問題を簡単にするために「二人の実力は全く同じである」という仮定を置きます。例えば平均1分でクリアできるゲームがあったとして、「55秒以内にクリアできる確率は30%」とか「1分以内にクリアできる確率は60%」とか、そういったものが各選手にあると考えます。その確率がどんなタイムに対しても全く同じであると考えます。この仮定を置くと、タイムの話ではなく次のような確率の話に置き換えても同じことになります。
二人は0から1までの任意の数字を同時に宣言する。それぞれが宣言した数字をa, bとする。(宣言するタイムに対応する)
また二人は0から1までの完全にランダムな数字を取得する。それぞれが取得した数字をx, yとする。(実際に走ったタイムに対応する)
宣言した数字が小さいほうを先手とする。先手は宣言した数字と取得した数字を比較する。成功(取得した数字のほうが小さい)した場合、先手の勝利。
先手が成功しなかった場合、後手も比較して成功したら後手の勝利。
どちらも成功しなかった場合、両者が取得した数字を比較し、小さいほうが勝利。
宣言する数字a, bは成功率と同じです。例えば0.2なら20%、0.7なら70%の確率で成功、といった具合です。二人の実力が全く同じでない場合、この問題の置き換えは成立しません。この数字宣言ゲームで「どんな数字を宣言するのが最も勝率を高められるか?」を考えるのが本記事の目的です。
1.2 最適な数字とは?
そもそも最も勝率が高くなる数字など存在するのでしょうか?ちょっと考えてみましょう。
例えば勇気を持って1を宣言するとします。これは成功率100%を意味し、タイムに置き換えるとかなり遅いタイム、どれだけ事故っても必ず突破できるタイムとなります。勝つ気がないように見えますが、相手が強気に0.3や0.4を宣言したらどうなるでしょうか。相手が成功しなければ勝ちなので、こちらの勝率は60%や70%となります。おや?思ったほど悪い戦略ではなさそうですね。しかし相手が0.9を宣言していたらどうでしょう。相手は90%の確率で成功するのですから、こちらの勝率は10%です。なるほど、こちらが1を宣言した場合、相手が0.5より大きい数字を宣言したら不利になります。では相手が0.5くらいを宣言すると読んだら何を宣言すべきでしょうか?0.45くらいかな?相手もこちらを読んで0.4くらいにするかもしれない…と、お互いに小さい数字を攻めようとすると今度は1宣言が強くなります。
このように相手が宣言する数字によってこちらが宣言すべき最適な数字も変化します。逆も然り。同じ数字を宣言しても相手次第で勝率は大きく変わります。そんなこと言ったら最適な数字なんてないじゃないか!と思うかもしれませんが、そうでもありません。
相手がどんな数字を宣言したとしても、最低でもこれだけの勝率は保証される、というような最低保証ともいえる勝率が存在します。例えばこちらが0.1、相手が1を宣言したらこちらの勝率は10%ですが、相手がどんな数字を宣言しても10%より小さくすることはできません(納得できない方はいろいろ数字を当てはめて考えてみましょう)。0.2を宣言したら20%は保証されます。この最低保証が最も高くするなるような数字が存在するはずです。その数字がいくつで、そのとき最低でもどれだけの勝率が保証されるのか?を考えることにします。先にネタバレしますが、0.5を宣言するのは最適ではありません。意外でしょうか?
2 解いてみる
2.1 先手視点
前置きがだいぶ長くなりましたが、そろそろ解いてみましょう。今回の問題は下の図を使うとわかりやすいです。この図は何かというと、座標(x,y)の色を見て、青ならa側が勝利、赤ならb側が勝利、という対応を表しています。ただしa<bとしています(つまりa側が先手)。

図全体としては辺の長さが1の正方形です。横軸をx、縦軸をyに対応させます。まず先手側の成功条件(x<aなら青)で区切り、次に後手側の成功条件(y<bなら赤)で区切り、最後に両者失敗時の勝利判定(x<yなら青、x>yなら赤)で区切れば完成します。青と赤の領域の面積がそれぞれの勝率と等しくなります。つまり面積を計算すれば勝率が求まります。確率の問題かと思っていたら図形の問題になりました。
青の領域の面積を計算してみましょう。図右側のように分割すれば「長方形+長方形+三角形」になるので、次式のようになります。

これはaを定数とすればbの二次関数です。今は先手視点で最悪のケースのときどうなるかを考えたいので、bを操作してSをできるだけ小さくすることを考えましょう。二次関数なのでb=aのとき面積は最大値をとり、bがaから離れるほど面積は小さくなります。a<bを前提にしていることと最大で1なことから、b=1のとき最小値のS=aを得ます(1行目に代入すると後半が全部0になってわかりやすい)。要するに後手は1を宣言したとき先手の勝率を最も下げられるということになります。
2.2 後手視点

次にa>bの場合、つまりa側が後手の場合を考えます。図の形も変わりますが、a<bの場合の図を縦横ひっくり返して色も反転させたものと同じになります。青の面積は「長方形+三角形」なので次式のようになります。

これはaを定数とすればbの一次関数です。bの係数が負なので、bが大きいほどSは小さくなります。ただしb<aのため、bを限りなくaに近づける、すなわちほぼb=aとしたとき最小値S=(1-a^2)/2を得ます。要するに先手は後手とほぼ同じ値を宣言したとき後手の勝率を最も下げられるということになります。
2.3 最適値を求める
ここで一度整理しましょう。a<b、すなわちa側が先手のとき、b側が1を宣言することでa側の勝率は最小になり、その勝率はa。またa>b、すなわちa側が後手のとき、bがaに限りなく近くaより小さい数を宣言することでa側の勝率は最小になり、その勝率は(1-a^2)/2。グラフにしてみましょう。

横軸はa、縦軸はaに対してbが最適な数字を宣言したときのa側の勝率です。つまり最低保証勝率がこのグラフです。最低保証を最も高くするために宣言すべき数字は、このグラフの頂点のx座標ということになります。2つのグラフの交点なので、次のように等式で繋げれば解けます。

0<x<1なのでプラス側を採用して、x=-1+√2となります。およそ0.4142…です。つまりだいたい41%くらいの成功率で成功するタイムを宣言すれば、相手がどんな数字を宣言しても少なくとも41%くらいの勝率が担保されるということになります。
ちょっとおかしいと思いませんか?二人が競うので二人の勝率を足したら1になるはずです。お互い同じ条件なら0.5ずつ。50%。それなのに41%くらいしか担保されないってどういうこと?と。
でも変ではありません。上の議論はb側が常にa側に刺さるような数字を宣言したときにa側の勝率がどうなるかを表したものです。要は後出しジャンケンできたらどうなるかを考えているので、a側の勝率がちょっと低くて当然です。相手がどんな数字を宣言しても、こちらの被害(?)が最小に抑えられるという意味で「最適」と言っているだけです。
3 ベストな戦略とは?
今回の計算でわかることはアルマゲドンルールに「安定」は存在しないということです。もし勝率50%が担保される数字があるなら皆がそれを宣言するだけになって意味がなくなるでしょう。なのでこれでいいと思います。どの数字を宣言するにしてもリスクとリターンがあるわけです。
様々なa, bの宣言のしかたに対するaの勝率を表にすると次のようになります。赤い部分はaが有利、青い部分はbが有利、白い部分は五分くらいです。計算方法は上のほうで求めたS1, S2に代入するだけです。

実際には0.1刻みではなく連続的な分布になりますが、便宜上0.1刻みのまま説明します。この表から読み取れることはいろいろありますが、一つずつ見ていきましょう。
0を宣言するメリットは無い
意味を考えれば当然です。成功するはずのないタイムを宣言するのはやめましょう。
相手よりちょっとだけ小さい数を宣言すると有利
上のほうに書いた「先手は後手とほぼ同じ値を宣言したとき後手の勝率を最も下げられる」がこれです。この傾向は数字が大きいほど顕著で、数字が小さいほど有利幅は小さくなります。この有利の取り方を便宜上「割り込み有利」と呼ぶことにします。相手の少し前に割り込んで先手を取る…みたいなイメージ。いい名前が浮かびませんでした。
0.4未満を宣言するメリットは少なめ
a=0.1~0.3の行を見ると、割り込み有利が取れない場合は大きな不利が付きやすいことがわかります。また、仮に有利が取れても数%程度なので誤差でしかありません。この数字帯を宣言する必要性が全くないわけではないですが、メリットは少ないと言えるでしょう。
0.4宣言はバランスが取れている
最適値の41.4%に近い0.4の行を見ると、0.3、0.9、1にしか不利になりません。0.3を宣言するメリットは少なく、0.9と1を宣言するのは後述しますがリスクが大きいです。仮に不利を取られても最悪40%で済むので、非常にバランスの取れた数字といえます。
0.5宣言もバランスは良いが環境がちょっと悪い
a=0.5の行も悪くないです。0.4宣言の弱点である0.9や1宣言に対し五分以上を取れて、弱点が0.3と0.4しかありません。しかし0.4のバランスが良いことから環境的には強くないかもしれません。それでも不利幅は少ないので、結局悪くないかもしれません。どうなんだろう(やってみないとわからない)
表では0.1刻みですが、もしa=0.5、b=0.4999…だった場合の勝率は37.5%になります。このようなケースを受け入れられるなら十分アリな選択肢だと思います。
1宣言はピーキー
1を宣言することは相手が攻めたタイムを宣言することを全力で期待することに等しいです。相手が0.5未満を宣言していればこちらが有利ですが、相手が0.5以上、特に1に近ければ近いほどこちらの勝率は大きく下がります。刺さればちょっと強いけど刺されると超弱い、というピーキーな数字です。
0.9宣言はリスクを抑えた1宣言
1宣言のピーキーさをちょっとだけ抑えるのが0.9宣言になります。相手の0.4宣言への有利幅減少、0.5宣言に微不利になる代わりに1宣言に超有利になります。ただし割り込み有利を取られたときの不利幅が大きいのは相変わらず。
0.8宣言以下は一点読み
0.8より小さい数の宣言は相手の0.4宣言に有利がつけられません。相手の0.9以上宣言にリスクを負わせるためだけの宣言になります。しかしこの数字帯でしか0.9以上宣言にリスクを負わせられないのも事実。弱いけど必要という難しいところです。
以上の関係を図にすると次のようになります。
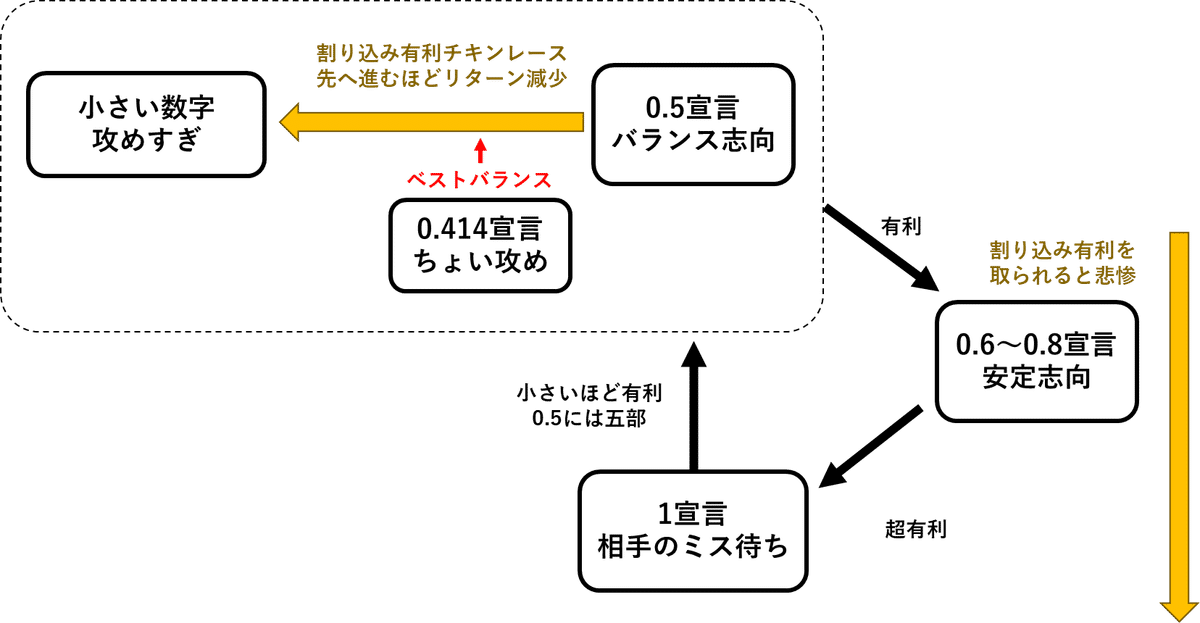
うまいこと3すくみのようになっています。じゃんけんのようですが、それぞれ勝った時のリターンと負けた時のリスクに大きな差があります。どの選択をするかはその人次第ですが、バランスが取れているのは0.41や0.5あたりのように思えます。失敗する可能性もそれなりにあるチャレンジングな宣言が最もバランスが良い、というアルマゲドンルール。非常によくできたルールだと感心しますね。
4 現実問題として
これまで色々と書いてきましたが、問題はいろいろあります。
自分と相手が全く同じ実力であるという仮定は現実にはありえない。平均タイムも分散も人によってさまざま。
仮に同じだとして、10回に4回くらいの確率で成功するタイムがいくつなのかを正確に把握している走者などほぼいない(と思う)。
勝率上は有利だとしてもその時いい走りができなければ意味がない。
実際に使えるかどうかは別として、アルマゲドンルールはこういう特性があるんだ、ということを理解しておくことは意味があると思います。
パズルとしては中々面白い問題でした。最適値を求めるまでは高校1年の数学(2次関数と最大値・最小値あたり)の知識で解けるので、問題設定も含めて入試問題になれるんじゃないかなーと思ったり。実力差がある場合も少し工夫すれば解けると思いますが、余力があればやります。
この記事が気に入ったらサポートをしてみませんか?
