DS56:クラスター分析【データサイエンティスト検定（リテラシーレベル）補習ノート】

2021年9月7日 09:26

データサイエンティスト検定（リテラシーレベル）の公式リファレンスブックで躓いたところをまとめていきます。

クラスタリングではデータ間の距離、そしてクラスター間の距離の測定方法にいくつかあるので、それぞれの特性を知ったうえで選ぶ必要があります。テキストには詳しく書かれていなかったので補足します。

2つのデータ間の距離の測定方法

ユークリッド距離：日常生活でいうところの距離です。特に理由がなければこれを使えばいいと思います。

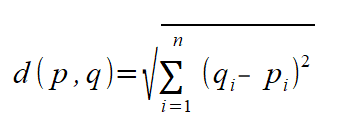
標準ユークリッド距離：テキストには出てきませんでしたが、ユークリッド距離を各次元ごとに標準偏差で割って標準化してから計算する方法です。次元ごとにスケールが違うときに役立つかと思います。

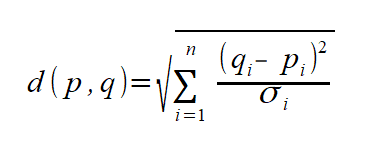
マンハッタン距離（シティブロック距離）：各座標の差の絶対値の総和を距離とします。碁盤の目の街で、ある目的地までクルマで移動する距離のイメージです。L1距離とも呼びます。

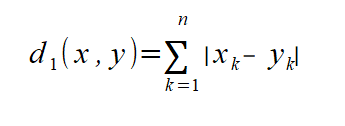
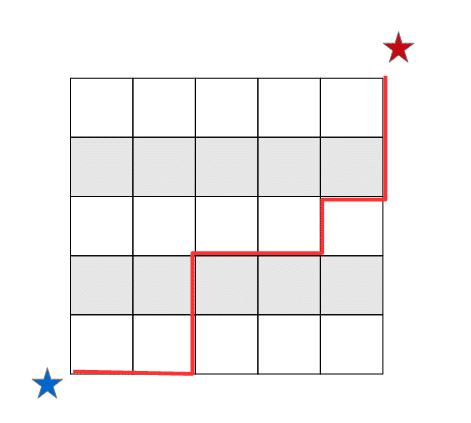
マンハッタン距離の使い道ですが、たとえば0,1で表されるようなデータが考えられます。

たとえば二択式のアンケートで次のような結果が得られたとします（yes=1,no=0）。AさんとBさん、およびBさんとCさんの回答には2つ（50%）の違いがあり、AさんとCさんは真逆の回答（100%の違い）になっています。

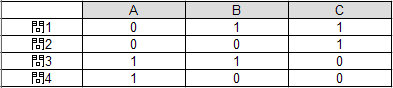
ここでユークリッド距離とマンハッタン距離を計算すると次のようになります。直観的にはAさんとBさんの距離と、AさんとCさんの距離は倍違うはずですが、ユークリッド距離にすると2÷√2=√2≒1.414倍しか違わないことになってしまいます。この場合、マンハッタン距離のほうが直観に近いといえます。

チェビシェフ距離（チェス盤距離）：各座標の差の絶対値の最大値を2点間の距離とします。L∞距離とも呼びます。

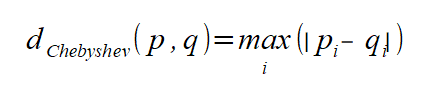
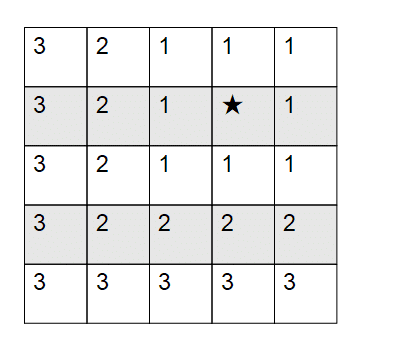
マハラノビノス距離：データの相関関係を考慮したうえで算出される距離です。変数間の相関が強いときに使うといいようです。下記の記事がわかりやすいかと思います。

テキストに記載されている測定方法を列記します。

ウォード法：結合後のクラスタの距離の分散から、結合前のクラスタの距離の分散をひいたもの。他の距離関数に比べて分類感度が高いので、よく使われるようです。

群平均法：結合後のクラスタ内にあるデータのすべての距離の平均を新たな距離とする方法。

最短距離法：結合されるクラスタ内にあるデータの最短距離を新たな距離とする方法です。外れ値に弱くなります。

重心法：クラスタの重心同士の距離を使う方法です。

メディアン法（中央値法）：重心法の簡易版で、重心のかわりに中央値を使う方法です。

こちらの記事がわかりやすかったです。

重心法やメディアン法はこちらの資料が参考になります。

この記事が気に入ったらサポートをしてみませんか？