感染者数の変曲点と実効再生産数の系統性を使ったピークアウトの予測

2020年9月21日　水野義之（京都女子大学）

要旨：

本稿では、新型コロナウイルスの感染者数が、一度増加に転じた後、ピークアウトする時期を予測するための、簡便な方法について解説する。この方法は統計誤差が小さいことが必要である。このため大都市圏など感染者数が多い場合に使うことができる。事例として2020年8月のピークアウトの予測を東京都、大阪府、神奈川県の場合に、約２週間前にできることを示した。
　ただし今後、本稿で想定していない社会変動やメディアの報道姿勢の変化（例えば日本のマスメディアも実効再生産数Rを報道する等）、あるいは国民の行動変容の考え方の変化、等が起こる可能性もある。その場合は本稿の方法は使えない可能性がある。しかし本稿で解説した考え方は、おそらく一部を変更して使える可能性もあることに注意したい。

１．はじめに：感染者数の増加とマスメディア

1.1　感染者の増え方のパターン

2020年9月現在、新型コロナの日々の新規陽性者数の増減のパターンには、５つの要因があると考えられる。それらは複雑に絡まっており、規則性はないようにも見える。しかし、この５成分の区別はデータ判断の上で必要であり、出発点だと私は思う。この５つの要因とは、次の通りである。

１）指数関数的に増大する成分（SIR方程式で説明できる）
２）１週間の周期（月曜が少ないなど）
３）日々の統計的なバラツキ（偶然この日に検査を受けたなど）
４）地域でクラスターが発生して突発的に増減する成分
５）生活変容で感染確率が変化して、増え方が変化することに伴う成分。

まず、何も対策をしない場合。感染症の拡大は、物理現象になり、SIRモデルに従うはずだ。つまり何もしないと、一定の増幅率で、増え続けると考えられる。その場合は、増えるだけ増える（仮に何も気づかなければ）。しかし実際には「何も対策しない」ことはあり得ない。逆に「仮に気づかないとすると」という場合。

仮に何も対策せず、感染者が増え続ける場合（仮に免疫が永続するなら）、感染を移す相手が次第にいなくなる。従って、やがて感染は広がらなくなり、終息（収束）する。しかし実際には、報道という社会的要因で、全国民の意識は、ほぼ同時に変化する。この結果、実効再生産数は、変化する、という結果になる。

1.2　行動変容とマスメディア報道

意識の変化の結果、社会的に起こる事は３通り。
１）外出の自粛。感染者が出歩いても、移す相手（非感染者S）が減る。
２）３密の回避。感染確率（β）を、局所的に下げたことに相当する。
３）マスク・手洗い。感染確率（β）を、平均的に下げたことに相当する。
どれも実効再生産数 Rを下げる。

実効再生産数は、R = Sβ/γとかける。ここでSは非感染者数で、移す相手の数。βは感染確率。またγは回復率。そこで、外出自粛は、このSを減らすことに対応する。他方で、３密を避けるとか、マスク・手洗いなどは、このβ（感染確率）を減らすことに対応する。（回復率γは一定と仮定する。）

つまり、この意識の変化（行動変容）は、結果的に、R（実効再生産数）を減らすことに対応することが分かる。逆に、仮に何もしなければ、Rは急には変化しない。そこで、仮にRが急に変化したとすると、これはマスコミが危ない（危なくない）と宣伝したからに違いないと推測できる。

1.3　実効再生産数の変化のパターン

この意味で、毎日の感染者数が増え始めると、マスコミが危ないと言い出す。そこで、みんなが気を付け始める。つまり上記の１）と２）と３）を注意して実行し、無意識的に「気をつけなければ」と思う。その結果、実効再生産数Rは減る。

「だれて」くると（つまり、自粛疲れ、あるいは慣れてくる、もう減ったと舐めてかかると）、皆が気を付け「なく」なる。その結果、Rは増えて、元に戻ってしまう。従って、こういう変化を繰り返す、ということが予想できる。

国民の行動変容の多くは、マスコミの「煽り方」で、決まってしまう。そしてそれは本当に見事に、そのように影響することがグラフから判る。この観察結果を、多少戯画的に描いたのが、次のツイートである。
https://twitter.com/y_mizuno/status/1288696779605565440

（ツイートの図）：

これを見ると、今後どう推移するか、見えてくるのではないだろうか。逆に、「日本はこういう戦略をとっている」という言い方もできる。つまり今後も、こうやって「騙し騙し」時間を稼いでワクチン開発を待つ、という感じであろうか。

1.4　Hammer and Dance戦略とは

この戦略をHammer and Dance戦略と呼ぶ。これは2020年4月上旬に、西村大臣もテレビで（ポロッと）口に出していた。日本政府はこう考えていることがわかる。9月中旬には小池都知事もハンマーアンドダンスとテレビで言っていた。公知の戦略である。

"Coronavirus: The Hammer and the Dance" (Tomas Pueyo)
https://medium.com/@tomaspueyo/coronavirus-the-hammer-and-the-dance-be9337092b56

日本語訳
https://medium.com/tomas-pueyo/%E3%82%B3%E3%83%AD%E3%83%8A%E3%82%A6%E3%82%A3%E3%83%AB%E3%82%B9-%E3%83%8F%E3%83%B3%E3%83%9E%E3%83%BC-%E3%81%A8-%E3%83%80%E3%83%B3%E3%82%B9-coronavirus-the-hammer-and-the-dance%E3%81%AE%E7%BF%BB%E8%A8%B3-4ddf02e500cd

The Hammer and the Danceとは。

１）ハンマーとは：仮に最初期に、感染者数が増えすぎてロックダウン（または緊急事態宣言）をした場合、それをハンマーで叩いて無理やり減らすという意味を込めて、「ハンマー」と呼ぶ。

２）ダンスとは：その後、人々は気を抜き、第二波が来るかもしれない。しかし「経験」もあるので、感染者数がそれほど増えないうちに、減らせる可能性が高い。このような、「第二波」以降の増え方＋減り方を、絵として見るとダンスしているように見えるので、「ハンマーとダンス」と呼ぶ。

次の図（出典は上記URL）の中に、どの時期が「The Hammer」で、どこが「The Dance」か、が記入してある。横軸は時間（日数）である。ブワン・ブワンと増減を繰り返す様子を、「ダンス」と呼んでいる。

２．実効再生産数の意味

2.1　実効再生産数の近似式

次に、東洋経済のサイト（https://toyokeizai.net/sp/visual/tko/covid19/）で使われる「実効再生産数の近似式」（西浦博教授の提案）の意味について。　計算式は「（直近7日間の新規陽性者数／その前7日間の新規陽性者数）^（平均世代時間／報告間隔）」。平均世代時間は5日、報告間隔は7日と仮定している。これは、どういう意味なのか。

この部分（出典は上記URL）を数式で書くと。
A = （直近7日間の新規陽性者数／その前7日間の新規陽性者数）、とおき、
x = （平均世代時間／報告間隔）、とおくと、元の式はAのx乗、これを、A^x と書く。ここで　^　は数字の右肩の上、つまり何乗するのか、という意味である。

さてそれで、これはどういう意味なのか。まず実効再生産数とは、「一人の人（感染者）が、治癒する間に、何人の人を感染させるか」という数だった。治癒する間（時間）に、というわけだ。この時間を、平均世代時間、と呼ぶ。

仮に、平均世代時間＝7日なら、指数の肩は 1なので、元の式は、（直近7日間の新規陽性者数／その前7日間の新規陽性者数）、つまり１週間（治癒する間）に何倍に増えているか、という数字である。つまり実効再生産数そのものだ。従って実効再生産数とは、大雑把には、増加の比の値であり、増加率（変化率）を意味する。

実際には、平均世代時間＝5日程度らしい。そんなわけで、（直近7日間の新規陽性者数／その前7日間の新規陽性者数）^（平均世代時間／報告間隔）という計算をしている。ここで、平均世代時間は5日、報告間隔は7日と仮定、している。

なぜ　^（平均世代時間／報告間隔）という冪乗をするのか。仮に、平均世代時間が1日だったとしよう。すると7日も経てば、実効再生産数の７回分なので７乗しないといけない。これでは実効再生産数の計算になっていないので、1/7乗して元に戻す（近似計算）。

2.2　S（非感染者数）とβ（感染確率）とR（実効再生産数）の意味

S（非感染者数）は、どこから取ってくれば良いか。元々は人口10万人といったような集団を想定していた。しかし現状では罹患率は0.1%もないので、近似的にS（非感染者数）は集団の全人口と近似できる。式の上では、Sは感染者数（＋回復者数）から逆算できると思っても良い。

βは、感染確率である。ある確率で感染するはず。確率は一定ではない。しかし平均すれば、感染させやすい感染症と、そうでない感染症があるから、それは、感染確率が違うと考える。その確率をβをおいた。この段階では、未知のパラメータである。（この値β自体は分からないが、Sβ/γという形で扱う。）

γは回復率である。これは小文字のガンマ（γ）、大文字のワイ（Y）ではない。平均して、何日で回復するか、例えば平均10日で回復するなら、1日あたりの回復率は1/10、単位は[1/日]。つまりこの場合γは、1日あたり1/10が平均で回復する。そういう数字がγである。

あとは自明だ。一人の感染者が、歩き回って、移す人数は、
１）移す相手＝非感染者Sが多いほど、多い。だからSに比例する。
２）感染確率βが高いほど、多い。だからβにも比例する。
従ってSβに比例する。しかし治癒もするので、γを引き算しないといけない。最終的に移す人の増加率は、Sβ-γとなる。

ここで、増加率 = Sβ-γ = γ (Sβ/γ - 1)　と変形して、このSβ/γ = R　と書く。これが実効再生産数Rである（RはRt、あるいはReとも書かれる）。実効再生産数Rが1ならば、増加率ゼロ、つまり感染者数が増える端から治るので、現状維持である。Rが1を超えると結果的に増加する。これが答えだった。

以上をまとめる。
１）感染確率βは、何もしない限り、変わらない。つまり感染者数は指数関数的に増え続ける（初期）。
２）しかし現代社会では、増加の途中で気付き、マスコミも騒ぎ、皆が気を付ける。
３）この結果βは減る。従って実効再生産数も減る。
４）つまり実効再生産数とは、社会意識の反映である。

３．ピークアウトの予測方法

3.1　ピークアウトを作るマスメディア報道

ここまでは、前置きである。2020年7月20日頃に私は、東京都の実効再生産数が減り始めたことに気づいた。この段階ではメディアは、東京で増え始めた事実に注目した。しかし私は、実効再生産数の変化トレンドに注目していた。なぜなら、実効再生産数が減るのは、簡単なことではないからだ。
https://twitter.com/y_mizuno/status/1287154481809854469

仮に何もしなければ、この新型コロナ感染症は、基本再生産数は2.5程度である。これは西浦教授がおっしゃっている通りだと、私も思う。逆に、この値（初期の実効再生産数の値）の2.5を減らすのは、社会的な「意識」のあり方、つまり国民の行動変容によるしかない、ということが理解できる。

感染者数がいつピークアウトするかは、この実効再生産数の減り方のトレンドを見れば、一目瞭然である。実効再生産数がいつ1を切るか、いつ、1以上から1以下に変化するか。傾向性を外挿すれば、予測できる。ただしある程度の中期的な継続性は、必須である。難しいのはこの見極めである。

この予測方法は、実効再生産数を減らす（感染確率を減らす）には、行動変容しかない、という事実認識と同時に、マスメディアによる情報伝搬が社会的にほぼ同時に、リアルタイムで起こる事実、従って実効再生産数は系統的に変化する、という仮定が、前提である。

このような仮定は、社会的な要因であるから、簡単に崩れることも理解する必要がある。予想が外れることも起こる。言うまでもない。外れる要因は、GoToキャンペーンなどで感染確率の減り方に社会的（人為的）な擾乱（撹乱）が加わった時。あるいはお盆の帰省なども同様だ。

3.2　東京都のピークアウト予測

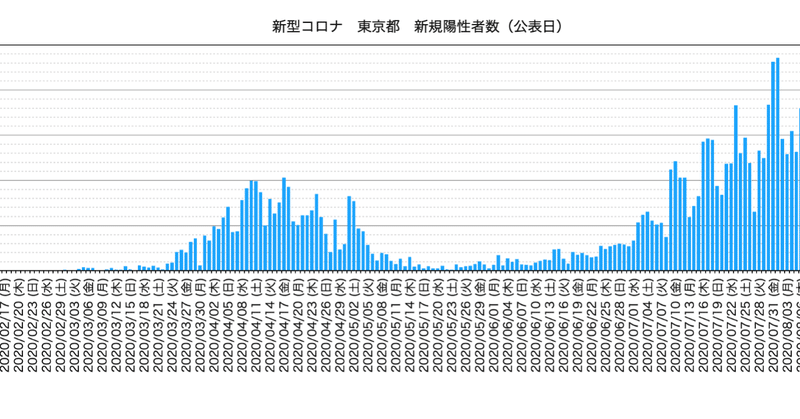
実際に東京都のデータで、この予測方法を示す。ここで7日での移動平均を取る人は多いが、これをやると、各データ点が統計的に独立ではなくなる。このため、ここでは単純に「7日ごと」で、まとめたデータを表示する。結果は次の通り。

ちなみに、どの7日を取るかで、データの見え方は微妙に変わる。ここでは、月曜日の発表データは週末（日曜）の数の反映だとした。つまり１週間を週末（月曜発表）までと考え、このグラフでは、火曜日から次の月曜までを、7日として合計とした。

まずは、元データをプロットしておく。これは9月7日段階の東京都ホームページでの数字である。これは見慣れた新規陽性者数の日々の推移である。

次の図（上）は、これを１週間で合計した数字である。図（下）には、その週の増加率を示した。ここで増加率の定義は、（ある週の合計）／（前の週の合計）ー１、である。従って、これに1を足して5/7乗すれば、東洋経済サイトの実効再生産数と一致する。基本的に両者は同じ傾向性を示す数字である。

この図から次の事が判る。
１）感染者数の推移をよく見ると7月13〜20日頃に変曲点がある（増え方が減り始めた）。
＊）変曲点とは、「下に凸」か「上に凸」かの「変わり目」の点である。
２）この「増え方の減り方」を延長すると、増え方＝０の点が予測できる。それは8月上旬となる。これがピークアウトである。

このような分析のツイートが、こちら。
https://twitter.com/y_mizuno/status/1287154481809854469
このツイートでは変曲点という言葉を使わなかったが、本稿の上の図には変曲点を記入した。変曲点ではグラフは「下に凸」から「上に凸」に変化する。変曲点では、変化率が増加から減少に転ずる（つまり増え方が鈍化する＝微分係数が増加傾向から減少傾向に転じる）。その時、変化の変化率（２次の微分）はゼロを切る。

実際に、2次の微分の値（2次差分の、元の平均値に対する割合）を縦軸、横軸を同じ日付にして、書いたのが次の図である。元のグラフの変曲点は、2次の微分＝ゼロの場所で起こる。なお2次の微分（2次導関数）は高校の数学IIIで学ぶ内容であるが、ご存知でない方にも雰囲気は理解できると思う。

3.3　大阪府のピークアウト予測

この意味で、ここで説明している方法は「感染者数の変曲点と実効再生産数の系統性を使ったピークアウトの予測」とでも命名できる。
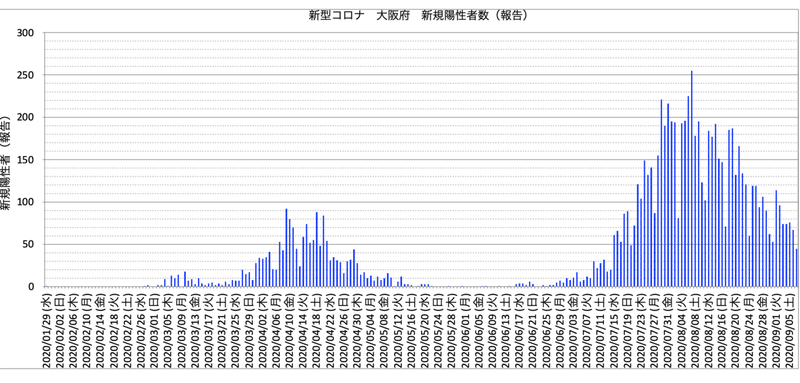
この方法を、大阪府の新規陽性者数に適用した。まず大阪府の新規陽性者数の報告値をプロットする。最後は9月7日である。

次に、
１）１週間ごとにまとめる。
２）週ごとの変化率を計算する（実効再生産数の計算に相当する）。
３）その実効再生産数の変化を見て、その系統性と、変曲点を調べる。
４）上の分析から実効再生産数＝1（増加率=0）となる時期（ピークアウトの時期）を予測する。
大阪府の場合に、これを行った結果を次の図に示す。上から順に、日々の新規陽性者数、増加率、そして2次の差分の率である。

この図から大阪府の場合も東京都と同様にして、約２週間前にはピークアウトの時期を予測できたはず、であることが分かる。つまり：
１）感染拡大の初期は指数関数的に増える。これを確認した上で、
２）7月20〜27日頃に変曲点がある（増え方が減少）。これも確認した上で
３）増え方の減少を外挿すると、「増え方＝０の点」（＝ピークアウト）は8月10日頃と予測できたはずである。

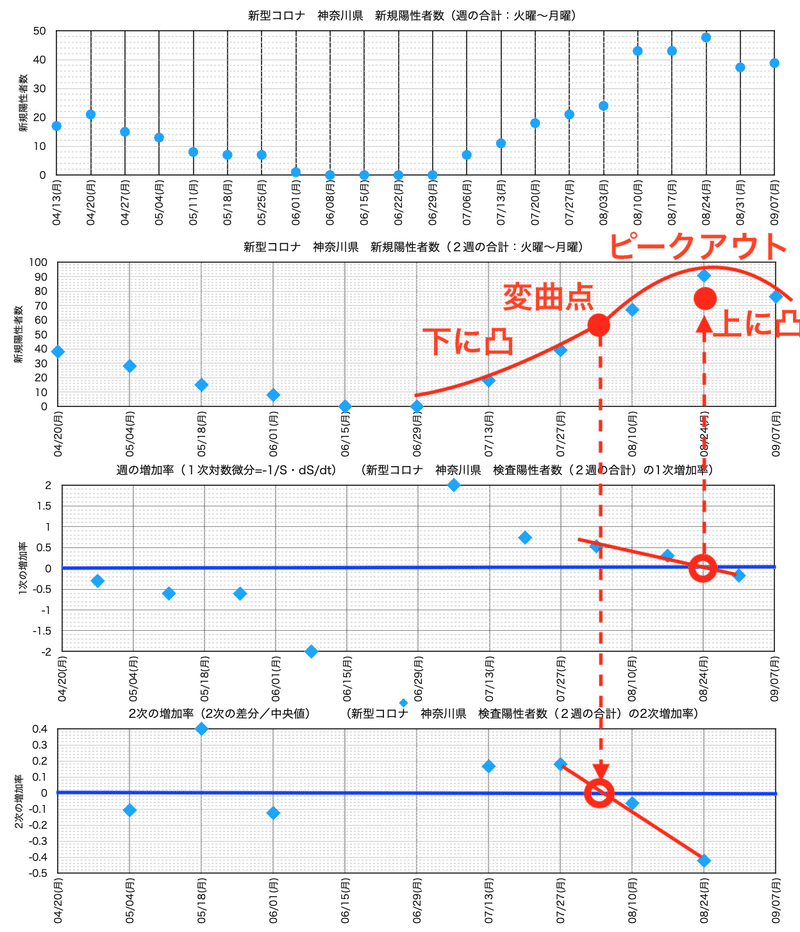
3.4　神奈川県の場合

次に神奈川県の場合も、同様にしてピークアウトを予測してみよう。
神奈川県はデータのばらつきが大きいので、２週間の合計をプロットする。結果は、東京都や大阪府と全く同じ方法で、ピークアウトが8月24日頃であったと、予測できたはずであったことが、次の図から理解できるだろうと思う。

４．まとめ

以上、本稿では、日々の新規陽性者数の公開データを使って、流行（第n波）のピークアウトがいつ起こるのか、予測する方法について解説した。もちろん、私が勘違いしている事項や、誤解している箇所もあるかもしれない。お気づきの点は、ご指摘をいただければ幸いだ。

ここで述べた予測方法と、それが使える条件について、まとめておきたい。

ピークアウトが予測できる条件と予測方法
１）第n波の感染初期であること。
言い換えると、

1-1）感染初期には、人々の注意レベルが低く、感染者数は指数関数的に増加するはずである。この指数関数的増加の傾向（「下に凸」の曲率）が見えていること。

1-2）初期の増加傾向がしばらく続くと、マスメディアの警告や注意喚起の声は大きくなる。これが起こっていること。

２）マスコミ報道に応じて、国民は注意レベルを上げ、３密回避やマスク・手洗いに、注意を傾けるに違いない。この結果、指数関数的な増加に変化が起こるはずである。

なぜなら、出歩く人は減り（非感染者数Sは減少し）、感染確率βも下がるからである。この結果は、実効再生産数Rの変曲点として、観察されるはずである。その変曲点を（目視でも良い）発見できること。

３）そこから実効再生産数は、系統的に下がり始めるはずである。この部分も観察できていること。

４）実効再生産数の系統的な低下は、しばらく続くはずである。なぜなら、マスメディアに反応するタイミングは全国民同時でも、危機感が人によって異なるからである。この低下傾向が続けば、あとは簡単。実効再生産数が1を横切る時期を目視で見当を付ける。それがピークアウトの予測時期である。

以上